Funções de Transferência no Simulink
Produzido por Gustavo BarbosaTeoria
Introdução
Bom dia, boa tarde ou boa noite! Animados para mais uma aulinha de SIMULINK? Hoje vamos aprender como construir diagramas de blocos com funções de transferência no SIMULINK.
“Ué, mas não vimos como criar funções de transferência usando só o MATLAB? Por que precisamos aprender a fazer isso no SIMULINK?”, você deve estar se perguntando.
É porque é mais prático usar o SIMULINK para modelar sistemas dinâmicos e controladores complexos, por causa da interface gráfica dele. No SIMULINK, conseguimos trabalhar com diagramas de blocos de forma bastante intuitiva, com ele já resolvendo a álgebra de blocos para nós.
Por isso, esta aula é o primeiro passo para aprendermos a projetar sistemas de controle super elaborados usando o SIMULINK. Partiu?

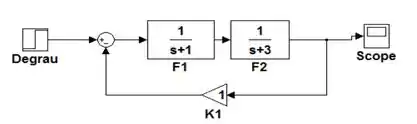
Antes de vermos como criamos funções de transferência no SIMULINK, vamos dar uma relembrada rápida em duas operações básicas da álgebra de blocos. A primeira operação é a de blocos em série, como os da figura abaixo. Quando temos dois blocos, cada um com uma função de transferência e , conectados um em seguida do outro, eles equivalem a um único bloco cuja função de transferência é o produto entre e :

A segunda operação é a de blocos em malha fechada, como na figura abaixo. Quando temos esta estrutura em um diagrama de blocos, ela equivale a um bloco com a expressão à direita da figura abaixo. Note que o sinal do denominador é o oposto do sinal do somador para o bloco de baixo (o bloco com ). Por exemplo, se o sinal do somador for negativo para , o sinal do denominador é positivo.
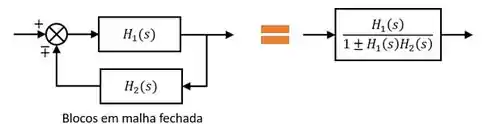
Normalmente, quando estamos trabalhando com diagrama de blocos “na mão”, temos que fazer várias operações como as apresentadas acima para chegar em um único bloco com uma função de transferência enooooorme.
No SIMULINK, podemos entrar com o diagrama de blocos original, sem fazer essas operações, para executarmos as simulações, o que diminui as chances de cometermos algum errinho.
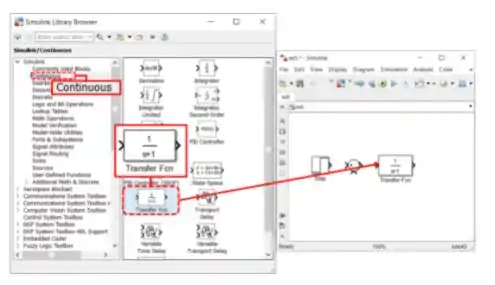
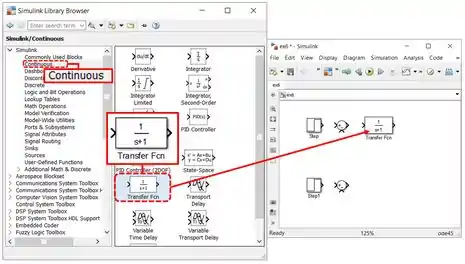
Criando funções de transferência no SIMULINK
No SIMULINK, usamos o bloco “Transfer Fcn” para criar uma função de transferência, que fica na biblioteca “Continuous”:

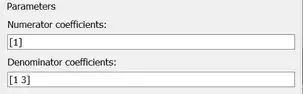
Vamos ver um exemplo para ver como esse bloquinho funciona. Vamos entrar com a função de transferência de 1ª ordem em um novo modelo do SIMULINK:
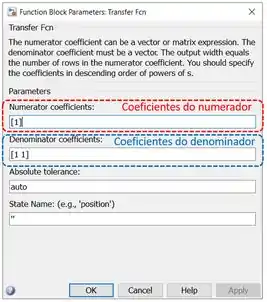
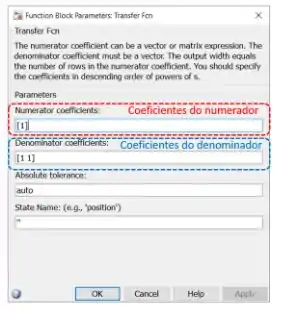
Arraste o bloco “Transfer Fcn” para o modelo em branco e dê um duplo-clique sobre ele, para ver seus parâmetros. Abrirá a janela abaixo:

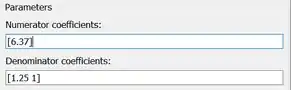
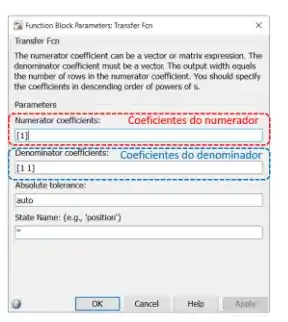
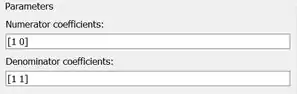
Para definir a função de transferência, você deve alterar os dois campos destacados na imagem acima. Neles, você deve entrar um vetor contendo os coeficientes do polinômio do numerador (campo destacado em vermelho, “Numerator coefficients”) e do denominador (campo destacado em azul, “Denominator coefficients”), indo do elemento do polinômio de maior ordem ao de menor ordem. Se você lembra como criar uma função de transferência no MATLAB, usando o comando , você deve ter notado que ele tem como entrada vetores assim.
Para a função de transferência , o polinômio do numerador é , logo, o vetor a ser entrado no campo destacado em vermelho da imagem acima é . Já o polinômio do denominador é , logo, o vetor a ser entrado no campo destacado em azul é .
Portanto, os parâmetros “Numerator coefficients” e “Denominator coefficients” ficarão assim:

Quando você clicar em “OK”, você verá que o bloquinho “Transfer Fcn” mudou de cara, apresentando a função de transferência que você definiu alterando as propriedades do bloco:
É bom nessa hora dar uma verificada se você entrou certinho com os coeficientes da função de transferência ;)
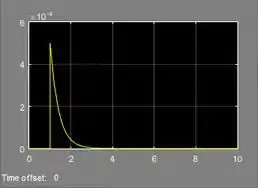
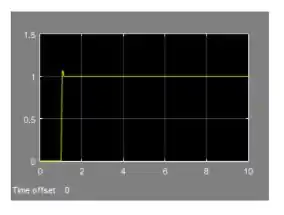
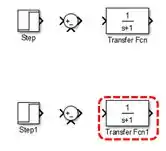
Para checar a resposta de uma função de transferência no SIMULINK, normalmente usamos um bloco “Step” e um bloco “Scope”:

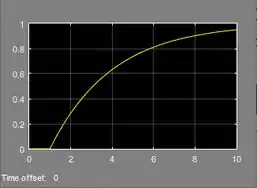
Vamos rodar a simulação e dar um duplo-clique sobre o “Scope” para vermos a resposta de ao degrau unitário:
Blocos em malha fechada
Vamos ver como criar um diagrama de blocos em malha fechada no SIMULINK, usando o seguinte diagrama como exemplo:

Onde:
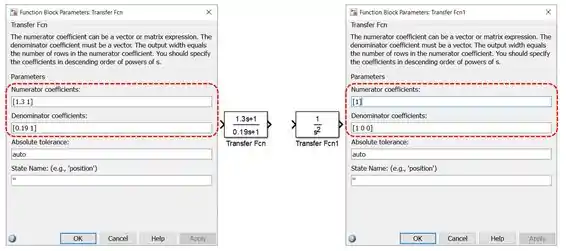
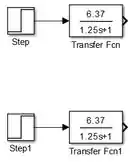
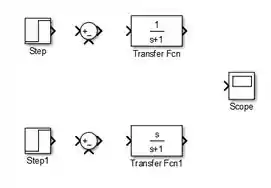
Vamos começar inserindo dois blocos “Transfer Fcn” em um novo modelo do SIMULINK e alterando os parâmetros deles, para entrar com e :
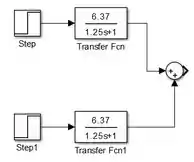
Em seguida, adicionamos um somador ao modelo indo à biblioteca “Math Operations” e selecionando o bloco “Sum”:

Note que o “Sum” tem duas entradas e uma saída, sendo que cada entrada tem um sinal de . Isso indica que o “Sum” vai somar dois sinais de entrada e vai fornecer o resultado por sua saída. Contudo, queremos fazer uma subtração, por isso, temos que alterar os parâmetros do bloco. Dê um duplo-clique sobre “Sum” para acessar seus parâmetros:
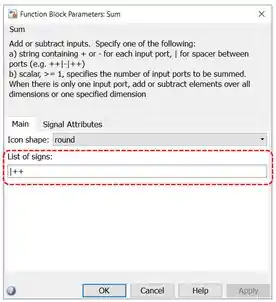
A propriedade que vamos alterar é a “List of signs”, destacada em vermelho acima. O padrão do “Sum” é a fazer a soma de dois sinais, por isso no campo “List of signs” temos . Para que seja feita a subtração de sinais, troque por . Clique em “OK” e você verá que o bloco mudou de cara:

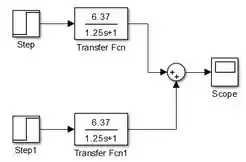
Vamos adicionar um bloco “Scope” como saída do modelo e conectar os blocos:

Precisamos fazer um ponto de derivação entre o bloco de e o “Scope”, para fechar a malha. Para isto, clique sobre a entrada de “Sum” que tem o sinal de menos e arraste. Aparecerá uma flecha vermelha tracejada:

Conecte a outra extremidade entre os blocos de e “Scope”:
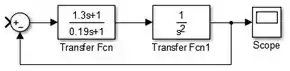
Pronto! Construímos o diagrama do modelo no SIMULINK. Vamos adicionar um bloco “Step” como entrada, para vermos a resposta do sistema ao degrau unitário:
Rodando a simulação, temos:

Viu como conseguimos modelar um diagrama de blocos um pouco mais complexo sem ter que fazer as operações de álgebra de blocos?
Hora de fazer os exercícios para praticar bastante e conseguir modelar qualquer parada ;D
Criando funções de transferência no SIMULINK
Blocos em malha fechada
Exercícios Resolvidos
Exercício Resolvido #1
“Adaptado de UFG & UCG – EEEC – Introdução ao Programa MATLAB com Aplicações, de Antônio César Baleeiro Alves, Enes Gonçalves Marra e José Wilson Lima Nerys (2007)”
Dada a função de transferência
Determine a resposta do sistema ao degrau unitário usando o SIMULINK.
Passo 1
Neste exercício, vamos praticar a criar modelos no SIMULINK com funções de transferência. Nosso modelo terá três blocos:
- A entrada do modelo será um bloco “Step”, simulando um degrau unitário;
- A função de transferência será incluída no modelo por meio do bloco “Transfer Fcn”;
- A saída do modelo será um bloco “Scope”, que mostrará a resposta do sistema ao degrau unitário.
Passo 2
Primeiramente, vamos inserir a entrada do modelo, um degrau unitário, em um novo modelo. Vá à biblioteca “Sources” do SIMULINK e arraste um bloco “Step” ao modelo em branco.
Como o enunciado não deu maiores detalhes sobre o degrau unitário, usaremos as propriedades padrão do bloco “Step” na simulação, que já é um degrau unitário. Por isso, não precisamos acessar seus parâmetros e já podemos entrar com no modelo.
Para isto, vá à biblioteca “Continuous”, encontre o bloco “Transfer Fcn” e arraste-o para o modelo:

Para definirmos , precisamos alterar os parâmetros do bloco “Transfer Fcn” que acabamos de inserir. Dê um duplo-clique sobre ele para ter acesso a suas propriedades:

Vamos alterar os dois campos destacados acima para definirmos . No campo destacado em vermelho, “Numerator coefficients”, devemos entrar um vetor com os coeficientes do polinômio do numerador de , indo do elemento do polinômio de maior ordem ao de menor ordem. Como o numerador de é simplesmente , não precisamos alterar a propriedade “Numerator coefficients”, pois este é seu valor padrão.
No campo destacado em azul, “Denominator coefficients”, devemos entrar um vetor com os coeficientes do polinômio do denominador, indo do elemento de maior expoente ao de menor expoente. O polinômio do denominador é , logo, o vetor a ser entrado no campo destacado em azul é .
Os parâmetros “Numerator coefficients” e “Denominator coefficients” ficarão assim:
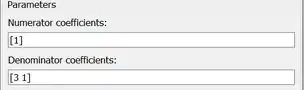
Clique em “OK” para salvar as alterações.
Passo 3
O próximo passo é inserir a saída do modelo, que será um bloco “Scope”, que nos apresentará a resposta do sistema. Vá à biblioteca “Sinks”, arraste para o modelo um bloco “Scope” e conecte os três blocos entre si. O modelo ficará assim:
O modelinho está pronto! Basta rodar a simulação para ver qual é a resposta de ao degrau unitário.
Resposta
Exercício Resolvido #2
“Adaptado de Sistemas Dinâmicos I: Usando a ferramenta MATLAB, da USP, elaborado por Eduardo L. L. Cabral e Larissa Driemeier. Exemplo p. 86”
Considere o sistema massa-mola-amortecedor (MMA) abaixo:
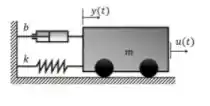
O corpo tem massa , o coeficiente de amortecimento é e a constante elástica da mola equivale a .
Considerando as condições iniciais nulas, o sistema tem a seguinte função de transferência:
No SIMULINK, gere o gráfico da resposta do sistema ao degrau unitário, executando uma simulação de .
Passo 1
Para vermos a resposta ao degrau unitário do sistema MMA, criaremos um modelo no SIMULINK com três blocos:
- A entrada do modelo será um bloco “Step”, simulando um degrau unitário;
- A função de transferência será incluída no modelo por meio do bloco “Transfer Fcn”;
- A saída do modelo será um bloco “Scope”, que mostrará a resposta do sistema MMA ao degrau unitário.
Precisaremos aumentar o tempo padrão de simulação de para e outros parâmetros de simulação para melhorar a resolução do gráfico da resposta do sistema MMA, produzido por “Scope”.
Passo 2
Vamos começar inserindo a entrada do modelo, que é um degrau unitário, em um novo modelo. Na biblioteca “Sources” do SIMULINK, encontre o bloco “Step” e arraste-o para o modelo em branco.
O bloco “Step” por padrão é um degrau unitário que se inicia a partir de Como o enunciado não especificou o instante em que o degrau começa, usaremos as propriedades padrão do bloco “Step” na simulação. Por isso, não precisamos acessar seus parâmetros e já podemos definir no modelo.
Vá à biblioteca “Continuous”, encontre o bloco “Transfer Fcn” e arraste-o para o modelo:
Vamos acessar os parâmetros do bloco “Transfer Fcn” que acabamos de inserir para definir , clicando duas vezes sobre ele:
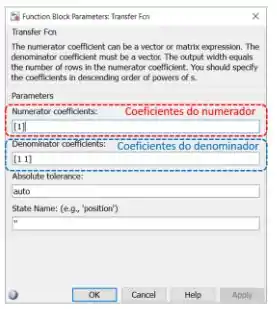
é definida alterando os dois parâmetros destacados acima. No campo destacado em vermelho, “Numerator coefficients”, devemos entrar um vetor com os coeficientes do polinômio do numerador de , indo do elemento do polinômio de maior ordem ao de menor ordem.
O polinômio do numerador de é , por isso, substitua por no campo destacado em vermelho.
No campo destacado em azul, “Denominator coefficients”, também devemos entrar um vetor, mas desta vez com os coeficientes do polinômio do denominador, indo do elemento de maior expoente ao de menor expoente.
O polinômio do denominador é , logo, o vetor a ser entrado no campo destacado em azul é .
Logo, os parâmetros “Numerator coefficients” e “Denominator coefficients” deverão ficar assim:
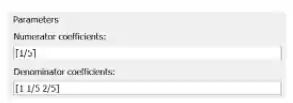
Clique em “OK” e você verá que o bloco “Transfer Fcn” mudou de cara:
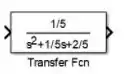
Ele agora contém em seu interior.
Passo 3
Agora vamos incluir a saída do modelo, um bloco “Scope”, que nos apresentará a resposta do sistema MMA ao degrau unitário. Vá a biblioteca “Sinks”, arraste para o modelo um bloco “Scope” e conecte os três blocos entre si. O modelo ficará assim:

A modelagem do sistema MMA está pronta! Antes de rodar o programa, precisamos ajustar o tempo de simulação de para . Na barra superior da janela do modelo, no campo onde podemos alterar o tempo de duração da simulação, destacado abaixo, troque por :
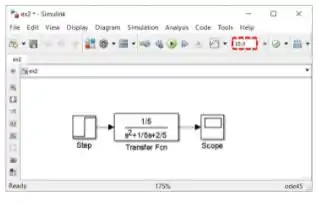
Execute a simulação e veja como ficou o gráfico, já ajustando sua escala, usando o botão “Autoscale” destacado abaixo, para ele ocupar toda a janela:

Passo 4
Note que a curva está meio pontiaguda. Para deixá-la mais “redondinha”, acesso os parâmetros de simulação, clicando sobre a engrenagem da barra superior da janela onde construímos os modelos, destacada em vermelho abaixo:

Na seção “Solver” da janela “Configuration Parameters”, estão os parâmetros de tamanho mínimo e máximo do passo do algoritmo da simulação (destacados em vermelho abaixo), que devem ser ajustados para deixar a curva mais redonda:
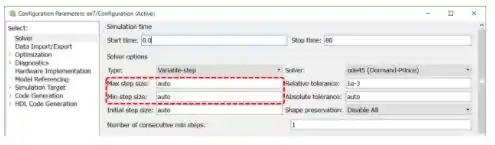
Os parâmetros “Max step size” (tamanho máximo de passo) e “Min step size” (tamanho mínimo de passo) são calculados automaticamente por padrão. Para termos curvas com maior resolução, isto é, mais “redondinhas”, devemos usar valores de passo bem pequenos, da ordem de . Eu adotei os valores abaixo, mas você pode usar os valores que quiser.

Clique em “OK”, feche a janela do “Scope” e rode a simulação de novo. Você verá que uma parte do gráfico “sumiu”, indicando que ocorreu o fenômeno de “amnésia”:
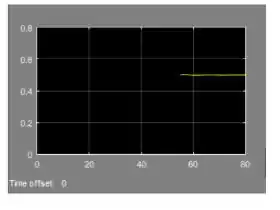
Passo 5
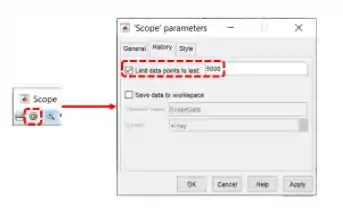
Para corrigir a amnésia, devemos mudar a propriedade “Limit data points to last” do bloco “Scope”.
Para acessar as propriedades de “Scope”, na janela do gráfico com um pedaço faltando, clique na engrenagem destacada abaixo. Uma janela chamada “Scope parameters” se abrirá. Vá na aba “History”, onde tem a propriedade “Limit data points to last”, destacada abaixo:
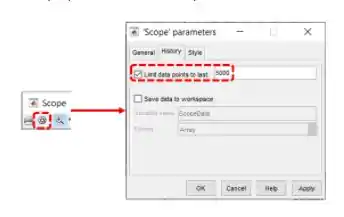
Vamos aumentar o valor do campo destacado em vermelho para corrigir a amnésia. Vamos mudar esse valor para , fechar a janela do “Scope” e executar a simulação de novo.
Quando você abrir o gráfico de novo, você verá que a curva vai estar completinha e bem bonitinha =)
Resposta

Exercício Resolvido #3
“Adaptado de UFSC – EMC – POSMEC – EMC6623000 Introdução ao Projeto de Controladores de Sistemas Mecânicos, ministrada por prof. Henrique Simas – Lista 10, ex. 5 (2018)”
Dada a função de transferência abaixo, que representa a dinâmica de um sistema que tem como entrada e saída :
No SIMULINK, esboce o gráfico de para uma entrada em degrau com amplitude .
Passo 1
Para plotarmos , usaremos o bloco “Transfer Fcn” para entrar com a função de transferência. Mas lembra como definimos uma função de transferência nesse bloco? Precisamos que o numerador e o denominador da função de transferência sejam poinômios, o que não é o caso do denominador, que tem dois termos entre parênteses que precisam ser multiplicados.
Para evitar a multiplicação dos termos, usaremos a operação de blocos em série, apresentada abaixo:

Nesta operação da álgebra de blocos, dois blocos em sequência, cada um com uma função de transferência e , equivalem a um único bloco cuja função de transferência é o produto entre e .
Contudo, usaremos essa operação no “sentido inverso”: vamos “quebrar” a função de transferência dada pelo enunciado em duas. Desta forma, não precisaremos multiplicar os termos do denominador para ter um polinômio só.
A função de transferência vai ser quebrada da seguinte forma:
Repare que se eu multiplicar por , eu tenho a função de transferência do enunciado.
Logo, nosso modelo no SIMULINK terá quatro blocos:
- A entrada do modelo será um bloco “Step”, simulando um degrau unitário;
- Dois blocos “Transfer Fcn”, uma para e outro para ;
- A saída do modelo será um bloco “Scope”, que mostrará a resposta ao degrau unitário.
Passo 2
Em um novo modelo do SIMULINK, insira um bloco “Step”, para simular a entrada , que é um degrau unitário.
Por padrão, o bloco “Step” é um degrau unitário que se inicia em Como o enunciado não especificou o instante em que o degrau começa, vamos deixar ele começando em mesmo. Desta forma, não precisamos alterar os parâmetros do bloco e podemos continuar a inserir blocos no modelo.
Vamos inserir um bloco “Transfer Fcn” para entrarmos com no modelo. Para isto, procure o bloco na biblioteca “Continuous” e arraste-o para o modelo:
Precisamos acessar os parâmetros do bloco “Transfer Fcn” que acabamos de inserir para definir , clicando duas vezes sobre ele:
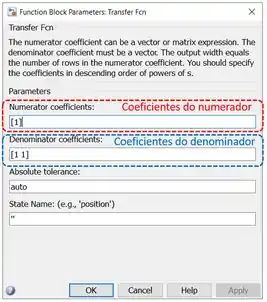
Uma função de transferência é definida alterando os dois parâmetros destacados acima. No parâmetro destacado em vermelho, “Numerator coefficients”, entramos com um vetor com os coeficientes do polinômio do numerador da função de transferência, indo do elemento do polinômio de maior ordem ao de menor ordem.
Já no parâmetro destacado em azul, “Denominator coefficients”, também entramos com um vetor, só que com os coeficientes do polinômio do denominador, indo do elemento de maior expoente ao de menor expoente.
O polinômio do numerador de é , por isso, substitua por no campo destacado em vermelho.
O polinômio do denominador é , logo, o vetor a ser entrado no campo destacado em azul é .
Portanto, os parâmetros “Numerator coefficients” e “Denominator coefficients” deverão ficar assim para :

Clique em “OK” e o bloco “Transfer Fcn” terá em seu interior:

Dica: se o polinômio for muito comprido, você pode aumentar o tamanho do bloco para ver a função de transferência inteira. Vá com o mouse sobre o bloco, clique em um dos cantos dele e arraste. Você verá que o bloco mudará de tamanho.
Passo 3
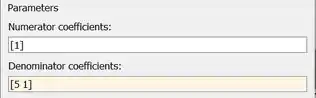
Insira um segundo bloco “Transfer Function” para entrar com e clique duas vezes sobre ele para transformá-lo em .
O numerador de é , igual ao valor padrão da propriedade “Numerator coefficients”, por isso, não precisamos alterar esse parâmetro.
O polinômio do denominador de é , logo, o vetor a ser entrado no campo da propriedade “Denominator coefficients” é .
Logo, os parâmetros de ficarão assim:
Clique em “OK” para salvar as alterações. Por enquanto, nosso modelinho está assim:

Passo 4
Falta adicionar o último bloco do modelo, que é a saída do sistema: um bloco “Scope”. Vá à biblioteca “Sinks” e arraste o “Scope” para o modelo. Em seguida, conecte os quatro blocos da seguinte forma:

É muito importante que os blocos “Transfer Fcn” sejam conectados em série, para termos a função de transferência do enunciado. Como o modelo acima é simples, conectá-los dessa forma pode parecer óbvio, mas é bom ter a operação dos blocos em série em mente quando estiver trabalhando com modelos maiores.
Com o modelo pronto, bora rodar a simulação! Quando a execução do programa terminar, dê um duplo-clique sobre “Scope” para ver o gráfico de . Não esqueça de ajustar a escala do gráfico clicando no botão “Autoscale”, na barra superior da janela do gráfico:
![]()
Resposta

Exercício Resolvido #4
“Adaptado do material de aula MATLAB Avançado – Simulink, do CEFET-MG, elaborado pelo prof. Carlos André Vaz Júnior. Exemplo 2.”
O tanque de nível abaixo está sob influência de perturbações degrau nas vazões de alimentação e :
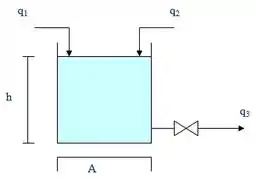
Onde é o nível da água e é a seção transversal do tanque, que tem um diâmetro . A vazão de saída é representada por e é controlada por uma válvula que atua sob uma resistência linear de .
A função de transferência que relaciona o nível da água à vazão de entrada é:
A função de transferência que relaciona o nível da água à vazão de entrada é igual a :
O nível é dado pela soma:
Considere que é um degrau de que se inicia em e que também é um degrau de , mas que se inicia em .
Usando o SIMULINK e considerando que o tanque está vazio em , determine o nível do tanque após .
Passo 1
O tanque é um sistema com duas entradas ( e ) e uma saída (o nível ). Para unirmos essas duas entradas e obtermos uma única saída, usaremos o bloco “Sum”.
Cada entrada tem sua própria função de transferência, resultando em um modelo com seis blocos:
- O sistema tem duas entradas, ambas degraus. Por isso, o modelo terá dois blocos “Step”. Contudo, eles terão parâmetros diferentes entre si, pois o degrau que representa inicia em e o outro, representando , em ;
- Cada uma das entradas será multiplicada por sua respectiva função de transferência, logo, o modelo terá dois blocos “Transfer Fcn”, um para e outro para ;
- As saídas dos blocos “Transfer Fcn” serão somadas por um bloco “Sum”;
- A saída do sistema será um bloco “Scope”, que os dará o gráfico de .
O enunciado pede para que simulemos o tanque por , dessa forma, podemos ver bem o impacto de sobre , quando ele se inicia em .
Um detalhe importante é que, como as unidades das grandezas do exercício estão em minutos, não precisamos fazer conversão alguma de minutos para segundos, que á a unidade de tempo que estamos acostumados a trabalhar no SIMULINK.
Passo 2
Vamos começar pelas entradas do sistema. Em um modelo do SIMULINK novo, insira dois blocos “Step” e alinhe-os verticalmente:

Precisamos alterar as propriedades deles, para que eles tenham as características de e dadas no enunciado.
Vamos dizer que o bloco de cima é , que é um degrau de amplitude de e se inicia em . Clique duas vezes no “Step” de cima para ter acesso a seus parâmetros:

Os parâmetros que devemos olhar são o “Step time”, destacado em vermelho acima, e os parâmetros “Initial value” e “Final value”, destacos dentro de um mesmo retângulo azul.
O “Step time” é o instante quando o degrau ocorre. Por padrão, ele é igual a . Como queremos que ocorra no instante , devemos alterar esse campo de para .
O parâmetro “Initial value” representa a amplitude do sinal antes que o degrau ocorra e por padrão é igual a . Vamos deixá-lo igual a pois o tanque deve estar vazio no começo da simulação.
O parâmetro “Final value” representar o valor do sinal após a ocorrência do degrau. Isso quer dizer que a diferença entre “Final value” e “Initial value” dá a amplitude do degrau. Por padrão, “Final value” é igual a . Como é um degrau de amplitude de , não precisamos alterar o valor padrão.
No final, os parâmetros do degrau representando ficam assim.

Clique em “OK” para registrar as mudanças e dê um duplo-clique no bloco “Step” de baixo do modelo, para definir . Lembrando que também é um degrau de , mas que se inicia em .
Devemos verificar os mesmos três parâmetros que verificamos no outro bloco “Step”: “Step time”, “Initial value” e “Final value”.
Como começa em , devemos alterar o “Step time” para . Já os parâmetros “Initial value” e “Final value” não precisam ser alterados, pelas mesmas razões que não mudamos seus valores padrão no bloco de cima.
No final, os parâmetros do bloco “Step” representando ficam assim:

Clique em “OK” para registrar as mudanças e fechar a janela de parâmetros.
Passo 3
Após inserirmos os blocos “Step” no modelo, devemos entrar com as funções de transferência e . Vá à biblioteca “Continuous” e arraste um bloco “Transfer Fcn” para o modelo:

Vamos inserir somente um bloco “Transfer Fcn”, pois basta definir com este bloco e em seguida copiá-lo e colá-lo para definir , já que e são iguais.
Dê um duplo-clique sobre o bloco “Transfer Fcn” que você acabou de incluir no modelo para ter acesso a suas propriedades:
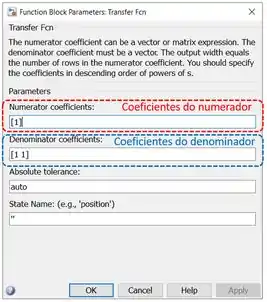
Para definir , vamos alterar os parâmetros “Numerator coefficients” (destacado em vermelho acima) e “Denominator coefficients” (destacado em azul). Ambos os parâmetros têm como entrada vetores com coeficientes de polinômios, indo do elemento de maior expoente ao de menor expoente. No caso de “Numerator coefficients”, são os coeficientes do polinômio do numerador da função de transferência. Já o vetor “Denominator coefficients” deve conter os coeficientes do polinômio do denominador da função de transferência.
O numerador de é , logo, devemos trocar o do campo destacado em vermelho por .
O polinômio do denominador é , onde é a área de seção transversal do tanque, que tem diâmetro . A área é a área de um círculo, que é calculada como:
Como , temos . Logo, o vetor a ser entrado no campo destacado em azul é .
No final, os parâmetros “Numerator coefficients” e “Denominator coefficients” de ficarão assim:
Clique em “OK” para registrar os novos parâmetros e fechar a janela de parâmetros de “Transfer Fcn”.
Com definido, como é igual a , você pode clicar no bloco “Transfer Fcn” que você acabou de alterar e dar um Ctrl+C para copiá-lo e um Ctrl+V para colá-lo no mesmo modelo. Desta forma, você terá dois bloquinhos iguais.
Aproveite para conectar cada bloco “Step” a uma entrada de um bloco “Transfer Fcn”. O modelo está assim, por enquanto:
Passo 4
Agora é hora de adicionarmos o bloco “Sum” para somarmos as saídas dos blocos “Transfer Fcn”! Vá à biblioteca “Math Operations”, encontre o bloco “Sum” e arraste-o para o modelo:

O bloco “Sum” por padrão tem duas entradas, cada uma com um sinal de . Isso indica que o “Sum” vai somar dois sinais de entrada e vai dar o resultado na sua saída. Como queremos somar dois sinais ( e ), não precisamos alterar as propriedades padrão de “Sum”.
Conecte a saída de cada bloco “Transfer Fcn” a um entrada de “Sum”. Desta forma, seu modelo ficará assim:
Passo 5
Para finalizar, vamos inserir a saída do modelo: um bloco “Scope”. Encontre-o na biblioteca “Sinks”, arraste-o para o modelo e conecte a sua entrada à saída do bloco “Sum”:
Modelo pronto! Falta só ajustar o tempo de simulação de (padrão do SIMULINK) para , no campo destacado abaixo:
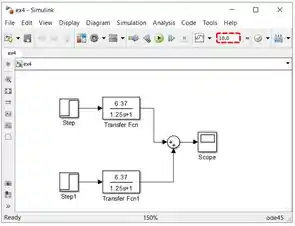
Execute a simulação e veja como ficou o gráfico. Já ajuste sua escala, usando o botão “Autoscale”, para ele ocupar toda a janela:

Passo 6
Para ver o nivel do tanque, vamos usar uma ferramenta que nos dá as coordenadas dos pontos do gráfico. Na barra de ferramentas da janela do “Scope”, onde temos o gráfico do nível do tanque, clique em “Try Time Scope”, indicado abaixo:
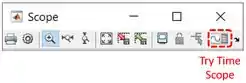
Aparecerão ferramentas novas para analisar o gráfico. Para vermos as coordenadas da curva, clique no botão “Cursor Measurements” com o ícone de uma régua, destacado abaixo:

Aparecerão duas retas verticais no gráfico, com bolinhas onde elas interceptam a curva, e uma janela à direita, indicando as coordenadas dessas bolinhas:

As retas são identificadas como e e na janela à direita, temos as coordenadas de tempo (eixo horizontal do gráfico) e nível (eixo vertical) da intersecção delas com a curva.
Clique na reta mais à direita, identificada como , e arraste-a até o final do gráfico. Você terá essas coordenadas:
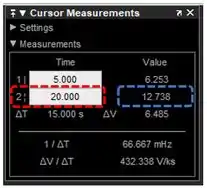
Destacado em vermelho, temos a coordenadas de tempo da reta e, em azul, temos a coordenada do eixo vertical da intersecção da reta com a curva. A coordenada de tempo é , logo, a coordenada do eixo vertical é o nível do tanque depois de . Desta forma, a resposta do exercício é a coordenada destacada em azul: o nível do tanque após é .
Resposta
O nível do tanque após é .
Exercício Resolvido #5
“Adaptado de USP e Texas A&M University - Simulink and block diagram – 2016 Brazil Study Abroad Program. Test #3 (2016)”
Considere o motor DC abaixo:

Ele tem como entrada a tensão e como saída, o ângulo . Considerando as constantes:
- Momento de inércia do motor e carga: ;
- Coeficiente de atrito do motor e carga: ;
- Resistência de armadura: ;
- Indutância da armadura: ;
- Constante elétrica: ;
- Constante de torque: .
Considerando as condições iniciais nulas, o motor DC tem como função de transferência:
Usando o SIMULINK, simule a resposta ao degrau em um sistema em malha fechada.
Passo 1
O enunciado nos fornece a função de transferência de um motor DC e pede para construirmos o sistema em malha fechada no SIMULINK. Em seguida, simularemos a resposta ao degrau do sistema em malha fechada que construímos.
Nosso modelo no SIMULINK terá quatro blocos:
- A entrada do modelo será um bloco “Step”, simulando um degrau unitário;
- Usaremos um bloco “Sum” para construirmos o sistema em malha fechada;
- A função de transferência será incluída no modelo por meio do bloco “Transfer Fcn”;
- A saída do modelo será um bloco “Scope”, que mostrará a resposta do sistema ao degrau unitário.
Passo 2
Em novo modelo do SIMULINK, insira um bloco “Step”, que servirá como entrada no nosso modelo. Como o enunciado não deu maiores especificações sobre o degrau, não vamos alterar as propriedades de “Step”.
Em seguida, insira um bloco “Sum”, para começarmos a construir o sistema em malha fechada. Você encontrará esse bloco na biblioteca “Math Operations”:

O bloco “Sum” tem duas entradas e uma saída. Por padrão, cada entrada tem um sinal de , indicando que o “Sum” vai somar dois sinais de entrada e a soma será fornecida pela saída do bloco. Contudo, em uma malha fechada, fazemos a subtração entre um sinal de referência (no caso, nosso bloco “Step”) e o resultado do produto entre esse sinal de referência e uma função de transferência (o sinal que sairá do bloco “Transfer Fcn” representando , como veremos mais pra frente).
Logo, temos que alterar os parâmetros do bloco. Dê um duplo-clique sobre “Sum” para acessar seus parâmetros. A propriedade que vamos alterar é a “List of signs”, destacada em vermelho abaixo:

Como o padrão do “Sum” é somar dois sinais, no campo “List of signs” temos . Para que seja feita a subtração de sinais, troque por . Clique em “OK” e você verá que o bloco vai ter esses sinais em seu interior:
Passo 3
O próximo passo é inserir no modelo. Vá à biblioteca “Continuous” e arraste um bloco “Transfer Fcn” para o modelo:
Para definir , dê um duplo-clique sobre o bloco “Transfer Fcn” que você acabou de incluir no modelo para ter acesso a seus parâmetros. Vamos mexer nos parâmetros “Numerator coefficients” (destacado em vermelho abaixo) e “Denominator coefficients” (destacado em azul).
Entramos vetores com coeficientes de polinômios, indo do elemento de maior expoente ao de menor expoente, em ambos os parâmetros. No “Numerator coefficients”, o vetor tem os coeficientes do polinômio do numerador de . Já o vetor “Denominator coefficients” contém os coeficientes do polinômio do denominador de .
O numerador de é , logo, devemos trocar o do campo destacado em vermelho por .
O polinômio do denominador é . Considerando as constantes dadas no enunciado, temos:
Logo, o vetor a ser entrado no campo destacado em azul é:
Portanto, os parâmetros “Numerator coefficients” e “Denominator coefficients” de ficarão assim:

Clique em “OK” para registrar as mudanças e fechar automaticamente a janela com os parâmetros. Você notará que o bloco “Transfer Fcn” tem agora em seu interior. Aumente o tamanho do bloco, selecionando-o e arrastando um dos seus cantos. Dessa forma, você conseguirá ver por completo. Por enquanto, nosso modelo está assim:

Passo 4
Vamos inserir a saída do modelo: um bloco “Scope”, para vermos o gráfico da resposta ao degrau do motor DC. Após adicionar o bloco “Scope”, conecte os blocos, primeiramente como se fosse uma malha aberta:

Para fechar a malha, clique sobre a entrada de “Sum” que tem o sinal de menos e arraste. Aparecerá uma flecha vermelha tracejada. Conecte a extremidade “solta” dessa flecha na linha entre o bloco com e o “Scope”, para criar um ponto de derivação:

Pronto! Temos o sistema em malha fechada e já podemos executar o programa, para ver a resposta ao degrau.
Após encerrar a execução, clique duas vezes sobre o “Scope” para ver o gráfico. Use o botão “Autoscale”, destacado abaixo, para ajustar a escala do gráfico.

Vixe, ele ficou bem esquisito.
Passo 5
O motivo de o gráfico ter ficado esquisito é que o número de dados calculados na simulação ultrapassou o limite padrão do bloco “Scope”. Para corrigir esse problema, temos que acessar as propriedades do bloco “Scope”, clicando na engrenagem destacada abaixo (que está na barra superior da janela do “Scope”), e mudar a propriedade “Limit data points to last”.
Ao clicar na engrenagem, o “Scope parameters” se abrirá. Vá à aba “History”, onde tem a propriedade “Limit data points to last”, destacada abaixo:
Desmarque a caixinha à esquerda, dentro do destaque em vermelho. Dessa forma, não haverá limite de dados e o gráfico ficará bonitão.
Clique em “OK” para registar a alteração, feche a janela do “Scope” e rode a simulação novamente. Ao abrir o gráfico, você verá que ele terá um formato que estamos mais acostumados a ver em exercícios de controle com entrada degrau.
Resposta
Exercício Resolvido #6
“Adaptado de USP e Texas A&M University - Simulink and block diagram – 2016 Brazil Study Abroad Program. Hands On! (2016)”
Considere o circuito RC abaixo:
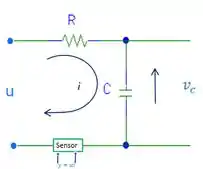
Onde , , a constante do sensor equivale a e é a corrente elétrica.
A entrada do sistema RC é uma tensão e a saída é . Quando desconsideramos o sensor, e a função de transferência do sistema é:
Quando o sensor é levado em consideração, e a função de transferência se torna:
Usando o SIMULINK, construa o diagrama de blocos em malha fechada do circuito RC para e e simule a resposta ao degrau para as duas malhas.
Passo 1
Neste exercício, construiremos dois diagramas de blocos em um mesmo arquivo do SIMULINK, para compararmos as respostas ao degrau. Um diagrama terá como função de transferência e o outro, .
Ambos os diagramas terão:
- Uma entrada, que será um bloco “Step”, simulando um degrau;
- Um bloco “Sum” para construirmos o sistema em malha fechada;
- Um bloco “Transfer Fcn” para entrarmos com a função de transferência.
A saída de ambos os diagramas será um bloco “Scope”, cujas propriedades alteraremos para ter os gráficos da resposta de e na mesma janela. Dessa forma, poderemos compará-los.
Passo 2
Vamos começar inserindo as entradas dos dois diagramas de blocos. Em um novo modelo no SIMULINK, insira dois blocos “Step”, um em cima do outro:

Em seguida, insira dois blocos “Sum”, um para cada sistema em malha fechada. Você encontrará esse bloco na biblioteca “Math Operations”:
O bloco “Sum” tem duas entradas e uma saída. Por padrão, o “Sum” soma dois sinais de entrada e o resultado é dado pela saída do bloco. A soma dos dois sinais é indicada pelo sinal de de cada entrada.
Em uma malha fechada, fazemos a diferença entre um sinal de referência (no caso, o bloco “Step”) e o resultado da multiplicação entre esse sinal de referência e uma função de transferência (o sinal que sairá dos blocos “Transfer Fcn” representando e , como veremos mais pra frente).
Por isso, temos que alterar os parâmetros do bloco. Dê um duplo-clique em um dos blocos “Sum” e mude a propriedade a “List of signs”, destacada em vermelho abaixo:
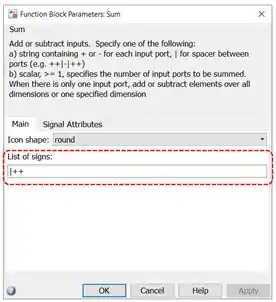
Para que seja feita a subtração de sinais, troque o por . Clique em “OK” e faça o mesmo procedimento para o outro “Sum”. Você verá que os sinais dos blocos mudaram:
Passo 3
O próximo passo é inserir e no modelo. Vamos fazer com que o diagrama de blocos de cima represente o circuito RC sem sensor, isto é, o diagrama de blocos de cima terá como função de transferência . Já o diagrama de blocos que ficará embaixo representará o circuito com sensor, ou seja, a função de transferência será .
Vamos começar por : vá à biblioteca “Continuous” e arraste um bloco “Transfer Fcn” para o modelo, alinhado com o “Step” e o “Sum” da parte de cima:
Para definir , dê um duplo-clique sobre o bloco “Transfer Fcn” que você acabou de incluir no modelo para acessar seus parâmetros. Vamos mexer nos parâmetros “Numerator coefficients” (destacado em vermelho abaixo) e “Denominator coefficients” (destacado em azul).

Esses parâmetros recebem vetores com coeficientes de polinômios, indo do elemento de maior expoente ao de menor expoente. No “Numerator coefficients”, o vetor tem os coeficientes do polinômio do numerador de . Já o vetor “Denominator coefficients” contém os coeficientes do polinômio do denominador de .
O numerador de é , logo, não precisamos mudar o do campo destacado em vermelho.
O polinômio do denominador é . Logo, também não precisamos alterar o campo destacado em azul, pois o vetor de coeficientes coincide com o padrão: .
Simplesmente clique em “OK”. Vamos construir o diagrama de blocos do circuito RC com sensor.
Passo 4
Insira um novo bloco “Transfer Fcn”, alinhado com os blocos “Step” e “Sum” de baixo:
Altere os parâmetros “Numerator coefficients” e “Denominator coefficients” do bloco que você acabou de inserir, atualizando os vetores com os coeficientes dos polinômios do numerador e do denominador de .
O numerador de é , logo, devemos trocar o do campo “Numerator coefficients” por .
O polinômio do denominador é igual ao de : . Logo, não precisamos alterar o campo “Denominator coefficients”, pois, novamente, o vetor de coeficientes coincide com o padrão: .
Dessa forma, os parâmetros “Numerator coefficients” e “Denominator coefficients” de ficam assim:
Clique em “OK” para registrar as alterações. Por enquanto, o modelo está assim:

Passo 5
Vamos inserir um bloco “Scope” para ser a saída de ambos os diagramas de blocos:
Precisamos que o “Scope” tenha duas entradas em vez de uma, para termos dois gráficos em uma mesma janela. Para isto, dê dois-cliques sobre o “Scope” para abrir sua janela e ter acesso aos seus parâmetros. Em seguida, clique na engrenagem destacada abaixo para abrir a janela com as propriedades do “Scope”.

Na aba “General” em “Scope parameters”, altere a propriedade “Number of axes” (destacada na imagem abaixo) de para e clique em “OK”. A janela do “Scope” ganhará mais um gráficos, como na imagem abaixo.
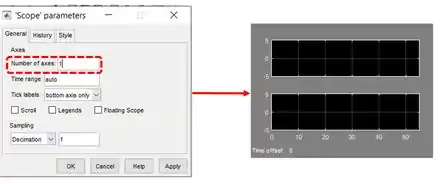
Feche a janela do “Scope” e veja que o bloco “Scope” ganhou uma setinha de entrada a mais:

Conecte os blocos como se fosse uma malha aberta, conectando a saída da “Transfer Fcn” com ) na entrada superior de “Scope” e a saída de “Transfer Fcn” com ), na entrada inferior de “Scope”:
Passo 6
Vamos fechar as malhas de ambos os diagramas. Para cada um deles, clique sobre a entrada de “Sum” que tem o sinal de menos e arraste, para surgir uma flecha vermelha tracejada. Conecte a extremidade “solta” dessa flecha na linha entre o bloco “Transfer Fcn” e o “Scope”, para criar um ponto de derivação:
Voilà! Modelo pronto! Agora é rodar a simulação, gerar os gráficos e ver as diferenças entre eles.
Resposta
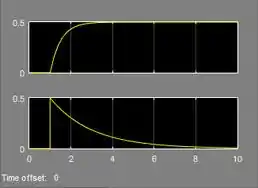
O gráfico de cima representa a resposta ao degrau do circuito RC desconsiderando o sensor. Já o gráfico de baixo é a resposta ao degrau considerando o sensor.
Exercício Resolvido #7
“Adaptado de UFSC – EMC – POSMEC – EMC6623000 Introdução ao Projeto de Controladores de Sistemas Mecânicos, ministrada por prof. Henrique Simas – Lista 8, ex. 3 (2018)”
O diagrama abaixo apresenta um sistema em malha fechada onde na realimentação existe um ganho :
Usando o SIMULINK, encontre o limite de de tal forma que a resposta no tempo em malha fechada se mantenha estável.
Passo 1
Neste exercício, reproduziremos o diagrama de blocos do enunciado no SIMULINK. Logo, o modelo terá seis blocos:
- A entrada do modelo será um bloco “Step”, simulando um degrau;
- Um bloco “Sum” para construirmos o sistema em malha fechada;
- Dois blocos “Transfer Fcn” para as funções de transferência e ;
- Um bloco “Gain” para entrarmos com o ganho ;
- A saída do modelo será um bloco “Scope”, para gerar o gráfico da resposta ao degrau.
Para encontrarmos o limite de , vamos ajustar o valor do bloco “Gain” até que o sistema se estabilize. A cada mudança de valor, rodaremos a simulação e usaremos o “Scope” para ver o gráfico da resposta ao degrau. Quando a resposta se tornar instável, encontraremos o limite de .
Passo 2
Em um modelo novo, insira um bloco “Step”. O enunciado não detalhou as propriedades do degrau, por isso vamos usar os parâmetros padrão do bloco.
Ao lado do bloco “Step”, insira um bloco “Sum”, para iniciar o sistema em malha fechada. Você encontrará esse bloco na biblioteca “Math Operations”:
Por padrão, as duas entradas de “Sum” tem um sinal de , indicando que o bloco vai somar os dois sinais de entrada. Em uma malha fechada, usamos o bloco “Sum” para subtrair dois sinais. Por isso, devemos alterar o parâmetro “List of signs” do bloco, destacado em vermelho abaixo. Dê um duplo-clique sobre “Sum” para acessá-lo:

Para que seja feita a subtração de sinais, troque por no campo destacado em vermelho e clique em “OK”.
Passo 3
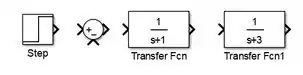
O próximo passo é inserir as duas funções de transferência no modelo. Vá à biblioteca “Continuous” e arraste dois blocos “Transfer Fcn” para o modelo, colocando-os em série, como na imagem abaixo:

Note que o bloco “Tranfer Fcn” mais à esquerda, representando , já é igual ao bloco que está na mesma posição no enunciado. Logo, não precisamos mexer em seus parâmetros e podemos partir para definir .
Dê um duplo-clique sobre o bloco “Transfer Fcn” mais à direita, que representará , para alterar os parâmetros “Numerator coefficients” (destacado em vermelho abaixo) e “Denominator coefficients” (destacado em azul).
Em ambos os campos destacados, entramos vetores com coeficientes de polinômios, indo do elemento de maior expoente ao de menor expoente. No “Numerator coefficients”, o vetor tem os coeficientes do numerador de . Já o vetor “Denominator coefficients” contém os coeficientes do denominador de .
O numerador de é , logo, não precisamos mudar o padrão de do campo destacado em vermelho.
O polinômio do denominador de é , logo, troque por no parâmetro “Denominator coefficients”:
Por enquanto, o diagrama de blocos está com essa cara:
Passo 4
Insira um bloco “Scope”, alinhado com os blocos anteriores, para gerar o gráfico da resposta ao degrau. Em seguida, conecte os blocos, como se fosse uma malha aberta:

Lembrando que o bloco “Step” deve se conectar à entrada com o do bloco “Sum”, já que é o sinal de referência da malha fechada.
Vamos adicionar ao diagrama o bloco que falta: o bloco “Gain”, pertencente à biblioteca “Math Operations”:
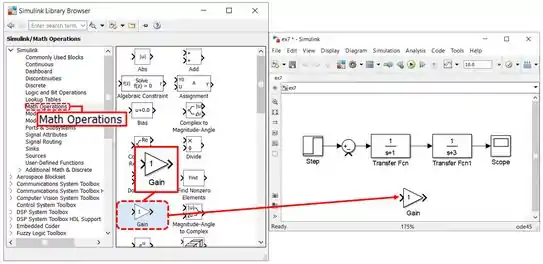
O bloco “Gain” tem uma entrada e uma saída. A entrada de “Gain”deve se conectar à saída de . Já a saída de “Gain” deve se conectar à entrada de “Sum” que tem o sinal , conforme a figura do enunciado.
Dica para deixar o diagrama mais organizado: podemos girar em um bloco no SIMULINK ao selecioná-lo e apertar Ctrl+R. Vamos fazer isso com o “Gain”, para ele ficar igualzinho ao diagrama no enunciado. Você vai acabar tendo que apertar Ctrl+R duas vezes para que o diagrama fique assim:

Bora fechar a malha? Conecte a saída de “Gain” à entrada de “Sum” restante:

Em seguida, clique sobre a entrada de “Gain” e arraste, para aparecer a flecha vermelha tracejada cuja extremidade “solta” você conectará na linha entre o bloco com e o “Scope”:
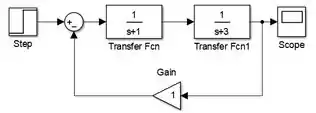
O diagrama de blocos está pronto!
Passo 5
Agora temos que ir ajustando o valor de “Gain”, que representa , para encontrarmos o valor máximo (ou mínimo) que pode assumir sem que o sistema se torne instável. Vamos começar com mesmo, que é o valor padrão (como podemos ver no diagrama que fizemos no SIMULINK).
Rode a simulação com o diagrama como ele está e veja o gráfico com a resposta:
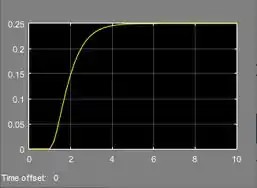
A resposta está bem estável, podemos alterar o valor de . Para isto, dê um duplo-clique sobre “Gain” e mude valor do parâmetro “Gain”, destacado em vermelho abaixo:
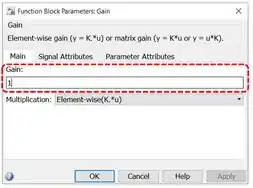
Vamos tentar usar valores maiores de . Troque por e veja que o “Gain” assumiu um novo valor no diagrama de blocos:

Rode a simulação novamente para ver o novo gráfico:
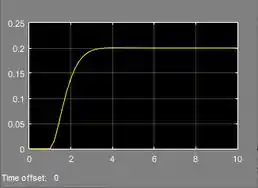
A resposta continua estável. Você pode continuar aumentando e verá que esse comportamento não muda: a resposta continuará estável.
Passo 6
Outra alternativa é diminuir , fazendo com que ele assuma valores negativos. Se você fizer , você terá:

Opa! A resposta não está mais parecida com o degrau, está parecendo uma rampa! Isso indica que estamos no limite da estabilidade. Se fizermos , por exemplo, , teremos:

Note que para , a resposta cresce indefinidamente e não se estabiliza, como podemos ver nos gráficos. Logo, deve ser maior que para que o sistema se mantenha estável.
Resposta
Para que o sistema se mantenha estável, .
Exercício Resolvido #8
“Adaptado de “An Engineer’s Guide to MATLAB: With Applications from Mechanical, Aerospace, Electrical, Civil, and Biological Systems Engineering” (3ª edição), escrito por Edward B. Magrab et al. Exercício 10.3, p. 607”
Suponha que um controlador é projetado usando um modelo simples como:
O controlador pode não estar modelado precisamente. Existe um modelo alternativo:
- Plote as respostas ao degrau em malha aberta de e ;
- Plote as respostas ao degrau em malha fechada de e , com um controlador proporcional de ganho .
Utilize um tempo máximo de .
Passo 1
Neste exercício, criaremos em um mesmo arquivo do SIMULINK dois diagramas de bloco, um para e outro para . Na letra a, vamos construir os diagramas malha aberta para vermos a resposta ao degrau. Ambos os diagramas em malha aberta terão:
- Uma entrada simulando um degrau, que será um bloco “Step”;
- Um bloco “Transfer Fcn” para entrarmos com a função de transferência ( ou ).
A saída de ambos os diagramas será um bloco “Scope”, que faremos ter duas entradas para comparar a resposta ao degrau de e .
Para fazer a letra b, incluiremos um bloco “Sum” em ambos os diagramas que construímos na letra a para fechar as malhas. Incluiremos també um bloco “Gain” para fazer um controlador proporcional nas malhas fechadas.
Passo 2
Vamos começar construindo os diagramas em malha aberta. Em um novo modelo no SIMULINK, insira dois blocos “Step”, um em cima do outro:
![]()
O próximo passo é inserir e no modelo. Vamos fazer com que a função de transferência do diagrama de blocos de cima seja . Já o diagrama de blocos que ficará embaixo terá como função de transferência .
Vá à biblioteca “Continuous” e arraste dois blocos “Transfer Fcn” para o modelo:

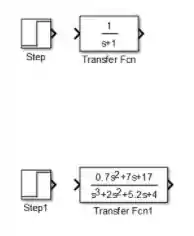
Note que o bloco “Tranfer Fcn” de cima, que representará , já tem por padrão a função de tranferência igual a . Logo, não precisamos mexer mais nele e podemos já definir .
Dê um duplo-clique sobre o bloco “Transfer Fcn” de baixo, que representará , para mudar os parâmetros “Numerator coefficients” (destacado em vermelho abaixo) e “Denominator coefficients” (destacado em azul).
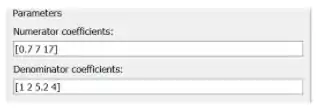
Em ambos os campos destacados, entramos vetores com coeficientes de polinômios, indo do elemento de maior expoente ao de menor expoente. “Numerator coefficients” receberá os coeficientes do numerador de e “Denominator coefficients”, os coeficientes do denominador de .
O numerador de é , logo, altere o do campo destacado em vermelho para .
O polinômio do denominador de é , logo, troque por no parâmetro “Denominator coefficients”.
Ao final, os parâmetros ficaram assim:
Clique em “OK” e aumente o bloco que contém , para ver a função de transferência por completo. Nosso modelo por enquanto está assim:
Passo 3
Vamos inserir um bloco “Scope” para ser a saída de ambos os diagramas:

Vamos adicionar mais uma entrada em “Scope”, para termos dois gráficos em uma mesma janela e podermos comparar as respostas. Para isto, dê dois-cliques sobre o “Scope” para abrir sua janela e clique na engrenagem destacada abaixo para acessar as propriedades do “Scope”.

Na aba “General” em “Scope parameters”, altere a propriedade “Number of axes” (destacada na imagem abaixo) de para e clique em “OK”.

Feche a janela do “Scope” e veja que o bloco “Scope” ganhou uma setinha de entrada a mais. Conecte os blocos de cada diagrama em série, como na imagem abaixo:
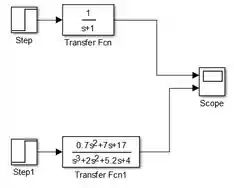
Da forma como os blocos estão conectados acima, a resposta ao degrau de estará no gráfico de cima da janela do “Scope”, e a resposta de , no gráfico de baixo.
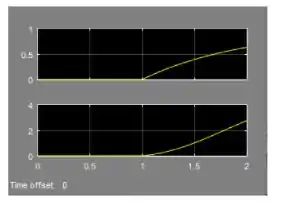
O modelo da letra a está pronto e podemos rodar o programa. Não esqueça de alterar o tempo de simulação para . Você terá as seguintes respostas ao degrau:
Desta forma, encerramos a letra a do exercício e podemos começar a fazer a letra b.
Passo 4
Para fazermos os diagramas de blocos da letra b, primeiro precisamos desconectar os blocos “Step” dos blocos “Transfer Fcn”, selecionando as flechas que os conectam e as deletando:
Em seguida, vamos inserir dois blocos “Sum”, um para cada sistema em malha fechada:

Devemos alterar as propriedades dos blocos “Sum”, para que eles façam a diferença entre o sinal de referência (o bloco “Step”) e o sinal de saída dos blocos “Transfer Fcn”. Desta forma, teremos dois diagramas em malha fechada.
Dê um duplo-clique em um dos blocos “Sum”, mude a propriedade a “List of signs” de para . Clique em “OK” e faça o mesmo procedimento para o outro “Sum”. O modelo ficará com essa cara:
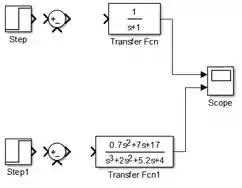
Passo 5
Para fazer o controlador proporcional, insira um bloco “Gain” entre o “Sum” e o “Transfer Fcn”, para cada diagrama de blocos, como na figura abaixo:

Precisamos alterar o valor dos blocos “Gain” para , pois foi pedido no enuciado. Dê um duplo-clique sobre cada um dos blocos “Gain” e mude valor do parâmetro “Gain” de para , no campo destacado abaixo:

Clique em “OK” para registrar as alterações e conecte os blocos de cada diagrama como se fosse uma malha aberta, como na imagem abaixo:
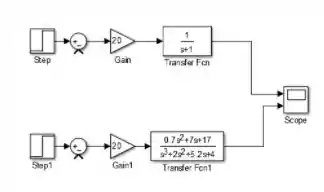
Passo 6
Vamos fechar as malhas de ambos os diagramas. Para cada um deles, clique sobre a entrada de “Sum” que tem o sinal , arraste para surgir a flecha vermelha tracejada e conecte a extremidade livre dessa flecha na linha entre o bloco “Transfer Fcn” e o “Scope”.
Pronto! Temos os diagramas em malha fechada com controlador proporcional exigidos pela letra b do exercício. Para vermos a resposta ao degrau, rode a simulação novamente:
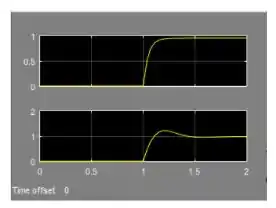
Resposta
- As respostas ao degrau de e em malha aberta são:
- As respostas ao degrau de e em malha fechada com um controlador proporcional com são:
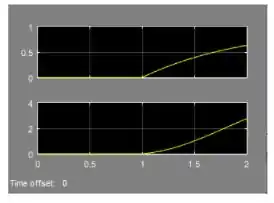

Sendo que o gráfico superior é a resposta de e o inferior, de . Note que enquanto as respostas em malha aberta são bem diferente entre si, as respostas em malha fechada são muito parecidas.