Diagrama de Nyquist
Produzido por Gustavo BarbosaTeoria
Introdução
E aí, controleiros de plantão? Tudo sob controle? Em uma graduação de engenharia as coisas ficam meio instáveis de vez em quando, né?

Se você estiver cursando alguma disciplina de Controle, vou tentar deixar as coisas um pouquinho mais estáveis para você. Hoje vamos aprender outra forma de usar o MATLAB para avaliar a estabilidade de um sistema dinâmico. Aprenderemos a plotar um gráfico de Nyquist e vamos relembrar o critério de Nyquist.
Primeiramente, vamos dar uma rápida revisada no que é o gráfico de Nyquist. Se quiser saber mais sobre o assunto ou precisar de uma revisão mais profunda, aqui no Responde Aí temos uma seção só sobre o critério de Nyquist, no capítulo Resposta em Frequência, no assunto Projeto de Controlador Clássico.
A análise do diagrama de Nyquist nos permite verificar a estabilidade de um modelo em malha fechada a partir da resposta do modelo em malha aberta. Normalmente, ele tem uma cara parecida com esta:
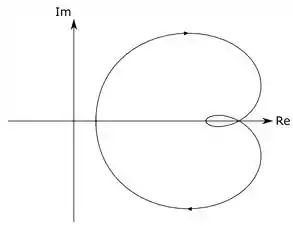
O diagrama de Nyquist é um gráfico no plano complexo, com a componente real no eixo horizontal e a componente imaginária no eixo vertical. Repare que as curvas do gráfico têm umas flechinhas, indicando um sentido de rotação (horário ou anti-horário). Essas flechinhas são importantes para o critério de Nyquist, que veremos mais adiante.
Plotando diagramas de Nyquist com o MATLAB
Agora que relembramos o que é um diagrama de Nyquist, vamos aprender a plotá-lo usando o MATLAB. O comando para gerar um diagrama de Nyquist a partir de uma função de transferência em malha aberta é bem diretão:
Ele tem como entrada uma função de transferência, criada usando o comando do MATLAB, e ele gera um gráfico com o diagrama de Nyquist para a .
Vamos fazer um exemplo no MATLAB, onde vamos gerar o diagrama de Nyquist da função de transferência:
Em um script novo, entre com no MATLAB usando a função , digitando as seguintes linhas de código:
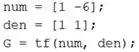
Na primeira linha, criamos um vetor em que cada elemento é um coeficiente do polinômio do numerador de , indo do componente com maior expoente () ao de menor expoente ().
Na segunda linha, criamos um vetor em que cada elemento é um coeficiente do polinômio do denominador de .
Na terceira linha, usamos a função para criar .
Para plotar o diagrama de Nyquist de , incluímos no script o comando:
![]()
Ao executar o programa, teremos o diagrama de Nyquist de :
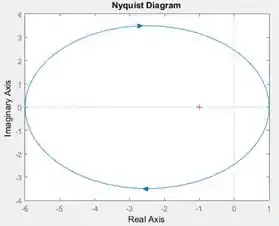
Foi pá-pum, né?
Reparou que o gráfico tem um cruzinha vermelha, bem no ponto com coordenadas ? É bem legal que o MATLAB nos dê essa cruzinha, pois ela vai ser essencial para avaliarmos a estabilidade do sistema pelo critério de Nyquist.
Estabilidade e critério de Nyquist
No critério de Nyquist, estabelecemos quantos polos positivos da função de transferência em malha fechada existem. O critério de Nyquist é dado pela equação:
Onde:
- é o número de polos positivos da função de transferência em malha fechada;
- é o número de voltas que o diagrama de Nyquist dá em torno de , exatamento o ponto marcado pela cruzinha vermelha no MATLAB;
- é o número de polos positivos da função de transferência em malha aberta.
O é obtido calculando as raízes do denominador da função de transferência em malha aberta e é obtido pelo diagrama de Nyquist. Há uma regrinha que diz que é positivo se a volta for no sentido horário. Se for no sentido anti-horário, é negativo.
Tendo e , calculamos . Lembra que um sistema estável não possui polos em malha fechada com parte real positiva? Logo, pelo critério de Nyquist, para que um sistema seja estável, deve ser igual a .
Vamos ver como o critério funciona com o nosso exemplo. Nossa função de transferência em malha aberta é:
O denominador de é , que tem como raiz . Logo, o único polo de é e ele é negativo. Portanto, não tem polos positivos e .
Vamos rever o diagrama de Nyquist de que geramos no MATLAB:
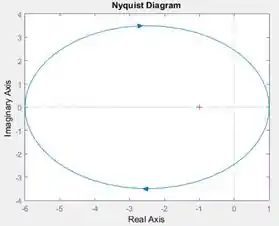
Note que o diagrama dá uma volta em sentido horário em torno da cruzinha vermelha, que marca o ponto . Portanto, .
Usando o critério de Nyquist, temos que . Como é diferente de , o sistema é instável.
Depois de aprender como plotar um diagrama de Nyquist no MATLAB e a avaliar estabilidade de um sistema usando o diagrama, tá na hora de praticar! Bora fazer os exercícios para fixar bem a aula de hoje ;D
Plotando diagramas de Nyquist com o MATLAB
Estabilidade e critério de Nyquist
Exercícios Resolvidos
Exercício Resolvido #1
“Adaptado de UFC – PET Engenharia Elétrica – Apostila de MATLAB – Exemplo p. 100 (2014)”
Usando o MATLAB, plote o diagrama de Nyquist da função de transferência:
Passo 1
O exercício pede para plotarmos o diagrama de Nyquist de usando o MATLAB. Para isto, devemos primeiro entrar com no MATLAB usando a função . Em seguida, usaremos a função para plotar o diagrama de Nyquist de .
Passo 2
O primeiro passo para resolver o exercício é entrar com no MATLAB. Para isto, usaremos a função , que cria funções de transferência e tem a seguinte sintaxe:
A função tem como entrada dois vetores, o primeiro contendo os coeficientes do polinômio do numerador da função de transferência (representado por ) e outro contendo os coeficientes do polinômio do denominador (representado por ). retorna um objeto representando a função de transferência, que será armazenada em .
Para , o polinômio do numerador é . Já o polinômio do denominador é .
Em um novo script, vamos criar duas variáveis representando os coeficientes dos polinômios, para servirem de entrada para . Como o polinômio do numerador tem somente um elemento correspondendo a , a variável representando seus coeficientes pode ser um número real. Chamaremos essa variável de e ela é igual a .
A outra variável é um vetor chamado , contendo os coeficientes de , indo do elemento com maior expoente ao de menor expoente:
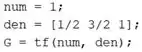
Logo abaixo, já digitamos o comando para criar , que será armazenado na variável .
Se quiser conferir se você entrou certinho, rode o programa que você tem até agora e peça para o MATLAB imprimir no Command Window. Se estiver tudo certo, você terá:

Passo 3
Tendo entrado com no MATLAB, podemos plotar seu diagrama de Nyquist, usando a função , que tem como sintaxe:
Ela tem como entrada uma função de transferência, criada usando o comando do MATLAB (representada por acima), e ela gera um gráfico com o diagrama de Nyquist para .
Adicione em seu código o comando:
![]()
Ao executar o programa, você terá o diagrama de Nyquist pedido pelo enunciado.
Resposta
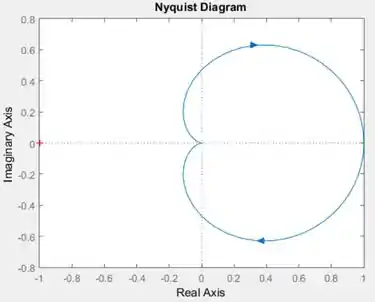
Exercício Resolvido #2
“Elaboração Própria”
Use o critério de Nyquist para determinar a estabilidade de um sistema com realimentação unitária e função de transferência mostrada abaixo:
Passo 1
O exercício pede para vermos se um sistema é estável ou não usando o critério de Nyquist. Para isto, usaremos a função do MATLAB para plotar o diagrama de Nyquist de e determinaremos a estabilidade do sistema usando o critério de Nyquist no gráfico gerado pelo MATLAB.
Passo 2
O primeiro passo para resolver o exercício é entrar com no MATLAB. Para isto, usaremos a função , que cria funções de transferência e tem a seguinte sintaxe:
A função tem como entrada dois vetores, o primeiro contendo os coeficientes do polinômio do numerador da função de transferência (representado por ) e outro contendo os coeficientes do polinômio do denominador (representado por ). retorna um objeto representando a função de transferência, que será armazenada em .
Para , o polinômio do numerador é . Já o polinômio do denominador é .
Em um novo script, vamos criar duas variáveis representando os coeficientes dos polinômios, para servirem de entrada para . Como o polinômio do numerador tem somente um elemento correspondendo a , a variável representando seus coeficientes pode ser um número real. Chamaremos essa variável de e ela é igual a .
A outra variável é um vetor chamado , contendo os coeficientes de , indo do elemento com maior expoente ao de menor expoente:

Logo abaixo, já incluimos o comando para criar , que será armazenado na variável .
Se quiser conferir se você entrou certinho, rode o programa que você tem até agora e peça para o MATLAB imprimir no Command Window. Se estiver tudo certo, você terá:

Passo 3
Tendo entrado com no MATLAB, podemos plotar o diagrama de Nyquist, usando a função , que tem como sintaxe:
Ela tem como entrada uma função de transferência, criada usando o comando do MATLAB (representada por acima), e ela gera um gráfico com o diagrama de Nyquist para .
Adicione em seu código o comando:
![]()
Execute o programa e você terá o diagrama de Nyquist de :
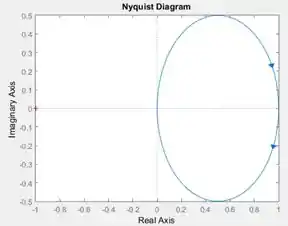
Passo 4
Com o diagrama de Nyquist em mãos, podemos avaliar a estabilidade do sistema usando o critério de Nyquist, que é dado pela equação:
Onde:
- é o número de polos positivos da função de transferência em malha fechada;
- é o número de voltas que o diagrama de Nyquist dá em torno de ;
- é o número de polos positivos da função de transferência em malha aberta.
Pelo critério de Nyquist, para que um sistema seja estável, deve ser igual a .
O é obtido calculando as raízes do denominador da função de transferência em malha aberta, no caso, . Neste exercício, o denominador de é , que tem como raiz . Logo, o único polo de é e ele é negativo. Portanto, não tem polos positivos e .
é obtido pelo diagrama de Nyquist. Vamos rever o diagrama de Nyquist gerado no passo anterior:

Tem uma cruzinha vermelha na extremidade esquerda do gráfico, reparou? Essa cruzinha marca o ponto de coordenadadas . Como a cruzinha está fora do diagrama de Nyquist (que é o círculo azul com flechinhas), o diagrama não dá volta alguma em torno de , logo,
Tendo e , calculamos . Temos que . Como , o sistema é estável.
Resposta
Sistema estável
Exercício Resolvido #3
“Elaboração Própria”
Use o critério de Nyquist para determinar a estabilidade de um sistema com realimentação unitária e função de transferência mostrada abaixo:
Passo 1
O exercício pede para vermos se um sistema é estável ou não usando o critério de Nyquist. Para isto, usaremos a função do MATLAB para plotar o diagrama de Nyquist de e determinaremos a estabilidade do sistema usando o critério de Nyquist no gráfico gerado pelo MATLAB.
Antes de usar , vamos entrar com no MATLAB usando a função . Lembra dela? Ela tem como entrada dois vetores com os coeficientes dos polinômios do numerador e do denominador da função de transferência. Repare que o denominador de está fatorizado. Logo, para podermos pegar os coeficientes dele, precisamos expandi-lo (isto é, multiplicar os termos) para gerarmos o polinômio. Por isso, antes de usarmos , faremos uma manipulação algébrica com o denominador de .
Passo 2
Para obter o polinômio do denominador de , vamos multipicar seus termos usando o MATLAB. Em um novo script, digite as linhas de código:
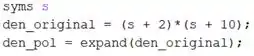
Na primeira linha, criamos uma variável simbólica .
Na segunda linha, entramos com o denominador de , armazenando-o na variável .
Na terceira linha, usamos o comando do MATLAB em . Este comando multiplicará os termos de e gerará o polinômio que precisamos, armazenando-o em .
Rodando o programa, temos:
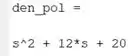
Passo 3
Agora que temos o polinômio do denominador de , podemos criar os vetores que servirão de entrada para . Lembrando que que tem como sintaxe:
A função tem como entrada dois vetores, o primeiro contendo os coeficientes do polinômio do numerador da função de transferência (representado por ) e outro contendo os coeficientes do polinômio do denominador (representado por ). retorna um objeto representando a função de transferência, que será armazenada em .
Para , o polinômio do numerador é . Já o polinômio do denominador é .
Em um novo script ou no script onde você obteve , vamos criar duas variáveis representando os coeficientes dos polinômios, para servirem de entrada para . Como o polinômio do numerador tem somente um elemento correspondendo a , a variável representando seus coeficientes pode ser um número real. Chamaremos essa variável de e ela é igual a .
A outra variável é um vetor chamado , contendo os coeficientes de , indo do elemento com maior expoente ao de menor expoente:
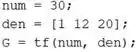
Logo abaixo, já incluimos o comando para criar , que será armazenado na variável .
É bom dar uma conferida em antes de continuar. Para isto, rode o programa que você tem até agora e imprima no Command Window:

Aparentemente, está tudo certinho. Podemos continuar :)
Passo 4
Tendo entrado com no MATLAB, podemos plotar o diagrama de Nyquist, usando a função , que tem como sintaxe:
Ela tem como entrada uma função de transferência, criada usando o comando do MATLAB (representada por acima), e ela gera um gráfico com o diagrama de Nyquist para .
Adicione em seu código o comando:
![]()
Execute o programa e você terá o diagrama de Nyquist de :
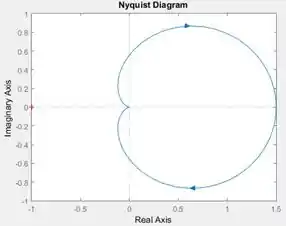
Passo 5
Com o diagrama de Nyquist em mãos, podemos avaliar a estabilidade do sistema usando o critério de Nyquist, que é dado pela equação:
Onde:
- é o número de polos positivos da função de transferência em malha fechada;
- é o número de voltas que o diagrama de Nyquist dá em torno de ;
- é o número de polos positivos da função de transferência em malha aberta.
Pelo critério de Nyquist, para que um sistema seja estável, deve ser igual a .
O é obtido calculando as raízes do denominador da função de transferência em malha aberta, no caso, . Para isto, é mais fácil a gente pegar o dado diretamente no enunciado, onde os termos do denominador não foram multiplicados:
Neste exercício, o denominador de é , que tem como raizes e . Logo, não tem polos positivos e .
é obtido pelo diagrama de Nyquist. Vamos rever o diagrama de Nyquist gerado no passo anterior:
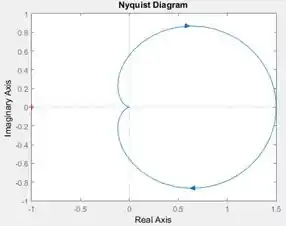
Tem uma cruzinha vermelha na extremidade esquerda do gráfico, reparou? Essa cruzinha marca o ponto de coordenadadas . Como a cruzinha está fora do diagrama de Nyquist (que é a curva azul com flechinhas), o diagrama não dá volta alguma em torno de , logo,
Tendo e , calculamos . Temos que . Como , o sistema é estável.
Resposta
Sistema estável
Exercício Resolvido #4
“Elaboração Própria”
Use o critério de Nyquist para determinar a estabilidade de um sistema com realimentação unitária e função de transferência mostrada abaixo:
Passo 1
O exercício pede para vermos se um sistema é estável ou não usando o critério de Nyquist. Para isto, usaremos a função do MATLAB para plotar o diagrama de Nyquist de e determinaremos a estabilidade do sistema usando o critério de Nyquist no gráfico gerado pelo MATLAB.
Antes de usar , vamos entrar com no MATLAB usando a função . Lembra dela? Ela tem como entrada dois vetores com os coeficientes dos polinômios do numerador e do denominador da função de transferência. Repare que o denominador de está fatorizado. Logo, para podermos pegar os coeficientes dele, precisamos expandi-lo (isto é, multiplicar os termos) para gerarmos o polinômio. Por isso, antes de usarmos , faremos uma manipulação algébrica com o denominador de .
Passo 2
Para obter o polinômio do denominador de , vamos multipicar seus termos usando o MATLAB. Em um novo script, digite as linhas de código:

Na primeira linha, criamos uma variável simbólica .
Na segunda linha, entramos com o denominador de , armazenando-o na variável .
Na terceira linha, usamos o comando do MATLAB em . Este comando multiplicará os termos de e gerará o polinômio que precisamos, armazenando-o em .
Rodando o programa, temos:
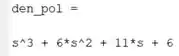
Passo 3
Agora que temos o polinômio do denominador de , podemos criar os vetores que servirão de entrada para . Lembrando que que tem como sintaxe:
A função tem como entrada dois vetores, o primeiro contendo os coeficientes do polinômio do numerador da função de transferência (representado por ) e outro contendo os coeficientes do polinômio do denominador (representado por ). retorna um objeto representando a função de transferência, que será armazenada em .
Para , o polinômio do numerador é . Já o polinômio do denominador é .
Em um novo script ou no script onde você obteve , vamos criar duas variáveis representando os coeficientes dos polinômios, para servirem de entrada para . Como o polinômio do numerador tem somente um elemento correspondendo a , a variável representando seus coeficientes pode ser um número real. Chamaremos essa variável de e ela é igual a .
A outra variável é um vetor chamado , contendo os coeficientes de , indo do elemento com maior expoente ao de menor expoente:

Logo abaixo, já incluimos o comando para criar , que será armazenado na variável .
É bom dar uma conferida em antes de continuar. Para isto, rode o programa que você tem até agora e imprima no Command Window:

Tudo certinho, bora plotar o diagrama de Nyquist ;)
Passo 4
Para plotar o diagrama de Nyquist, use a função , que tem como sintaxe:
Ela tem como entrada uma função de transferência, criada usando o comando do MATLAB (representada por acima), e ela gera um gráfico com o diagrama de Nyquist para .
Adicione em seu código o comando:
![]()
Execute o programa e você terá o diagrama de Nyquist de :

Passo 5
Com o diagrama de Nyquist em mãos, podemos avaliar a estabilidade do sistema usando o critério de Nyquist, que é dado pela equação:
Onde:
- é o número de polos positivos da função de transferência em malha fechada;
- é o número de voltas que o diagrama de Nyquist dá em torno de . é positivo se a volta for no sentido horário. Se for no sentido anti-horário, é negativo.
- é o número de polos positivos da função de transferência em malha aberta.
Pelo critério de Nyquist, para que um sistema seja estável, deve ser igual a .
O é obtido calculando as raízes do denominador da função de transferência em malha aberta, no caso, . Para isto, é mais fácil a gente pegar o dado diretamente no enunciado, onde os termos do denominador não foram multiplicados:
Neste exercício, o denominador de é , que tem como raizes , e . Logo, não tem polos positivos e .
é obtido pelo diagrama de Nyquist. Vamos rever o diagrama de Nyquist gerado no passo anterior:

Tem uma cruzinha vermelha no gráfico, reparou? Essa cruzinha marca o ponto de coordenadadas . Vamos dar um zoom na região da cruzinha, para ver quantas voltas o diagrama de Nyquist dá em torno dela:

O diagrama de Nyquist (representado pela curva azul) dá duas voltas em torno da cruzinha, ambas em sentido horário, logo, .
Tendo e , calculamos . Temos que . Como é diferente de , o sistema é instável.
Resposta
Sistema instável
Exercício Resolvido #5
“Adaptado de UFRGS – Departamento de Engenharia Elétrica – ENG04450 – Sistemas de Controle: Laboratório I – Introdução ao MATLAB. Profs. João Manoel Gomes da Silva e Romeu Reginatto (2002)”
Use o critério de Nyquist para determinar a estabilidade de um sistema com realimentação unitária e função de transferência mostrada abaixo:
Passo 1
O exercício pede para vermos se um sistema é estável ou não usando o critério de Nyquist. Para isto, usaremos a função do MATLAB para plotar o diagrama de Nyquist de e determinaremos a estabilidade do sistema usando o critério de Nyquist no gráfico gerado pelo MATLAB.
Antes de usar , vamos entrar com no MATLAB usando a função . Lembra dela? Ela tem como entrada dois vetores com os coeficientes dos polinômios do numerador e do denominador da função de transferência. Repare que o denominador de está fatorizado em parte. Logo, para podermos pegar os coeficientes dele, precisamos expandi-lo (isto é, multiplicar os termos) para gerarmos o polinômio. Por isso, antes de usarmos , faremos uma manipulação algébrica com o denominador de .
Passo 2
Para obter o polinômio do denominador de , vamos multipicar seus termos usando o MATLAB. Em um novo script, digite as linhas de código:
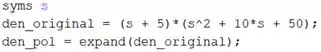
Na primeira linha, criamos uma variável simbólica .
Na segunda linha, entramos com o denominador de , armazenando-o na variável .
Na terceira linha, usamos o comando do MATLAB em . Este comando multiplicará os termos de e gerará o polinômio que precisamos, armazenando-o em .
Rodando o programa, temos:

Passo 3
Agora que temos o polinômio do denominador de , podemos criar os vetores que servirão de entrada para . Lembrando que que tem como sintaxe:
A função tem como entrada dois vetores, o primeiro contendo os coeficientes do polinômio do numerador da função de transferência (representado por ) e outro contendo os coeficientes do polinômio do denominador (representado por ). retorna um objeto representando a função de transferência, que será armazenada em .
Para , o polinômio do numerador é . Já o polinômio do denominador é .
Em um novo script ou no script onde você obteve , vamos criar duas variáveis representando os coeficientes dos polinômios, para servirem de entrada para . Como o polinômio do numerador tem somente um elemento correspondendo a , a variável representando seus coeficientes pode ser um número real. Chamaremos essa variável de e ela é igual a .
A outra variável é um vetor chamado , contendo os coeficientes de, indo do elemento com maior expoente ao de menor expoente:

Logo abaixo, já incluimos o comando para criar , que será armazenado na variável .
É bom dar uma conferida em antes de continuar. Para isto, rode o programa que você tem até agora e imprima no Command Window:

Estando tudo nos conformes, podemos partir para o próximo passo, que é plotar o diagrama de Nyquist.
Passo 4
Para plotar o diagrama de Nyquist, use a função , que tem como sintaxe:
Ela tem como entrada uma função de transferência, criada usando o comando do MATLAB (representada por acima), e ela gera um gráfico com o diagrama de Nyquist para .
Adicione em seu código o comando:
![]()
Execute o programa e você terá o diagrama de Nyquist de :
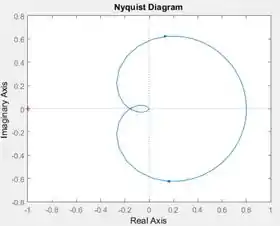
Passo 5
Com o diagrama de Nyquist em mãos, podemos avaliar a estabilidade do sistema usando o critério de Nyquist, que é dado pela equação:
Onde:
- é o número de polos positivos da função de transferência em malha fechada;
- é o número de voltas que o diagrama de Nyquist dá em torno de . é positivo se a volta for no sentido horário. Se for no sentido anti-horário, é negativo.
- é o número de polos positivos da função de transferência em malha aberta.
Pelo critério de Nyquist, para que um sistema seja estável, deve ser igual a .
O é obtido calculando as raízes do denominador da função de transferência em malha aberta, no caso, . Para isto, é mais fácil a gente pegar o dado diretamente no enunciado, onde os termos do denominador não foram multiplicados:
Neste exercício, o denominador de é e tem três raízes. A primeira raiz é fácil de achar: é . Para encontrar as duas raízes restantes, do polinômio de grau , vamos usar a função do MATLAB, que tem como sintaxe:
Ela tem como entrada o vetor , que contém os coeficientes do polinômio cuja raízes queremos encontrar, indo do elemento com maior expoente ao de menor expoente. O comando retorna as raízes do polinômio e as armazena em .
No nosso exercício, queremos encontrar as raízes de . Logo, o vetor é:
Vamos adicionar no nosso script do MATLAB o comando para acharmos as raízes:
![]()
Executando o programa, temos que as raízes de são dois números complexos:

Logo, as três raízes do denominador são , e . Quando temos zeros que são números complexos, avaliamos a parte real do número. Como a parte real das raízes e é negativa, , não tem polos positivos e .
Passo 6
é obtido pelo diagrama de Nyquist. Vamos rever o diagrama de Nyquist gerado no passo :

Tem uma cruzinha vermelha na extremidade esquerda do gráfico, reparou? Essa cruzinha marca o ponto de coordenadadas . Como a cruzinha está fora do diagrama de Nyquist (que é a curva azul com flechinhas), o diagrama não dá volta alguma em torno de , logo,
Tendo e , calculamos . Temos que . Como , o sistema é estável.
Resposta
Sistema estável
Exercício Resolvido #6
“Elaboração Própria”
Use o critério de Nyquist para determinar a estabilidade de um sistema com realimentação unitária e função de transferência mostrada abaixo:
Passo 1
Vamos avaliar se um sistema é estável ou não usando o critério de Nyquist. Para isto, usaremos a função do MATLAB para plotar o diagrama de Nyquist de e, a partir do gráfico, veremos a estabilidade do sistema usando o critério de Nyquist.
Antes de usar , usaremos a função para entrar com no MATLAB. Como o denominador de está fatorizado, precisamos expandi-lo para sabermos como será a entrada de . Por isso, antes de usarmos , vamos multiplicar os termos do denominador de .
Passo 2
Vamos multipicar os termos do denominador de usando o MATLAB. Em um novo script, digite as linhas de código:

Na primeira linha, definimos uma variável simbólica .
Na segunda linha, entramos com o denominador de , armazenando-o na variável .
Na terceira linha, usamos o comando do MATLAB em . Este comando multiplicará os termos de e gerará um polinômio, que é armazenado em .
Rodando o programa, temos:
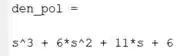
Passo 3
Após expandir o denominador de , vamos criar os vetores que servirão de entrada para , que tem a sintaxe:
A função tem como entrada dois vetores, o primeiro contendo os coeficientes do polinômio do numerador da função de transferência (representado por ) e outro contendo os coeficientes do polinômio do denominador (representado por ). retorna um objeto representando a função de transferência, que será armazenada em .
Para , o polinômio do numerador é . Já o polinômio do denominador é .
Em um novo script ou no mesmo script onde foi calculado, vamos criar duas variáveis com os coeficientes dos polinômios, que serão a entrada de . Como o polinômio do numerador tem somente um elemento correspondendo a , a variável representando seus coeficientes pode ser um número real. Chamaremos essa variável de e ela é igual a .
A outra variável é um vetor chamado , contendo os coeficientes de , indo do elemento com maior expoente ao de menor expoente:

Logo abaixo das linhas onde as variáveis e foram criadas, já colocamos o comando para criar , que será armazenado em .
Uma dica: confira antes de continuar, pra ver se não digitou nada de errado. Para isto, rode o programa que você tem até agora e imprima no Command Window:
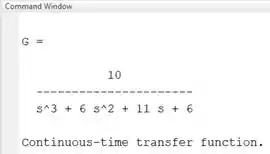
Estando tudo certinho, podemos plotar o diagrama de Nyquist de .
Passo 4
Para plotar o diagrama de Nyquist, use a função , que tem como sintaxe:
Ela tem como entrada uma função de transferência, criada usando o comando do MATLAB (representada por acima), e ela gera um gráfico com o diagrama de Nyquist para .
Adicione em seu código o comando:
![]()
Execute o programa e você terá o diagrama de Nyquist de :
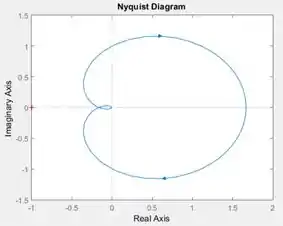
Passo 5
Com o diagrama de Nyquist plotado, podemos utilizá-lo para avaliar a estabilidade do sistema por meio do critério de Nyquist, que é dado pela equação:
Onde:
- é o número de polos positivos da função de transferência em malha fechada;
- é o número de voltas que o diagrama de Nyquist dá em torno de . é positivo se a volta for no sentido horário. Se for no sentido anti-horário, é negativo.
- é o número de polos positivos da função de transferência em malha aberta.
Pelo critério de Nyquist, para que um sistema seja estável, deve ser igual a .
O é obtido calculando as raízes do denominador da função de transferência em malha aberta, no caso, . Para isto, é mais fácil a gente pegar o dado diretamente no enunciado, onde os termos do denominador não foram multiplicados:
Neste exercício, o denominador de é , que tem como raízes , e . Logo, não tem polos positivos e .
é obtido pelo diagrama de Nyquist. Vamos rever o diagrama de Nyquist gerado no passo anterior:
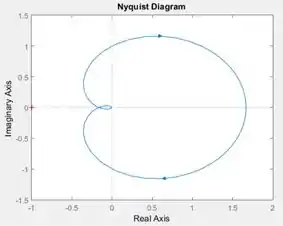
Note a cruzinha vermelha na lateral esquerda do gráfico. Essa cruzinha marca o ponto de coordenadadas . Como a cruzinha vermelha está fora do diagrama de Nyquist (representado pela curva azul), o diagrama não dá volta alguma em torno dela, por isso, .
Tendo e , calculamos . Temos que . Como é igual a , o sistema é estável.
Resposta
Sistema estável
Exercício Resolvido #7
“Elaboração Própria”
Use o critério de Nyquist para determinar a estabilidade de um sistema com realimentação unitária e função de transferência mostrada abaixo:
Passo 1
Vamos avaliar a estabilidade de um sistema usando o critério de Nyquist. Para isto, usaremos a função do MATLAB para plotar o diagrama de Nyquist de e, a partir do gráfico, veremos a estabilidade do sistema usando o critério de Nyquist. Mas antes de usar , precisamos entrar com , por meio da função .
Passo 2
A função serve para criar funções de transferência e tem como sintaxe:
Ela tem como entrada dois vetores, o primeiro contendo os coeficientes do polinômio do numerador da função de transferência (representado por ) e outro contendo os coeficientes do polinômio do denominador (representado por ). retorna um objeto representando a função de transferência, que será armazenada em .
Para , o polinômio do numerador é . Já o polinômio do denominador é .
Em um novo script, vamos as entradas de . Como o polinômio do numerador tem somente um elemento correspondendo a , a variável contendo seus coeficientes pode ser um número real. Chamaremos essa variável de e ela é igual a .
A outra variável é um vetor chamado , contendo os coeficientes de , indo do elemento com maior expoente ao de menor expoente:

Logo abaixo das linhas onde e foram criados, já digitamos o comando para criar , que será armazenado em .
Antes de continuar, verifique pra ver se não digitou nada de errado. Para isto, rode o programa que você tem até agora e imprima no Command Window:

Estando tudo OK, podemos plotar o diagrama de Nyquist.
Passo 3
Use a função para gerar o diagrama de Nyquist, que tem como sintaxe:
Ela tem como entrada uma função de transferência, criada usando o comando do MATLAB (representada por acima), e ela gera um gráfico com o diagrama de Nyquist para .
Adicione em seu código o comando:
![]()
Execute o programa para ver o diagrama de Nyquist de :
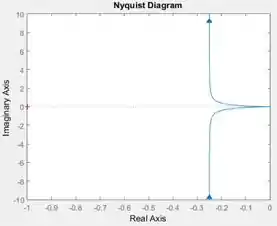
Meio esquisito, né? Talvez você se assuste com esse formato diferente do que vimos nos exercícios anteriores, mas você vai ver no próximo passo que a análise do diagrama pelo critério de Nyquist não tem nada de diferente do que vimos até aqui.
Passo 4
Vamos utilizar o diagrama de Nyquist plotado para avaliar a estabilidade do sistema por meio do critério de Nyquist, que é dado pela equação:
Onde:
- é o número de polos positivos da função de transferência em malha fechada;
- é o número de voltas que o diagrama de Nyquist dá em torno de . é positivo se a volta for no sentido horário. Se for no sentido anti-horário, é negativo.
- é o número de polos positivos da função de transferência em malha aberta.
Pelo critério de Nyquist, para que um sistema seja estável, deve ser igual a .
O é obtido calculando as raízes do denominador da função de transferência em malha aberta, no caso, :
O denominador de é , que tem como raízes e . Logo, não tem polos positivos e .
é obtido pelo diagrama de Nyquist. Vamos rever o diagrama de Nyquist gerado no passo anterior:
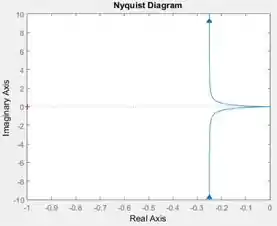
Note a cruzinha vermelha na lateral esquerda do gráfico. Essa cruzinha marca o ponto de coordenadadas . Como a cruzinha vermelha está fora do diagrama de Nyquist (representado pela curva azul), o diagrama não dá volta alguma em torno dela, por isso, .
Tendo e , calculamos . Temos que . Como é igual a , o sistema é estável.
Resposta
Sistema estável
Exercício Resolvido #8
“Elaboração Própria”
Use o critério de Nyquist para determinar a estabilidade de um sistema com realimentação unitária e função de transferência mostrada abaixo:
Passo 1
Neste exercício, vamos avaliar a estabilidade de um sistema usando o critério de Nyquist. Para isto, usaremos a função do MATLAB para plotar o diagrama de Nyquist de e aplicaremos o critério de Nyquist no diagrama para ver se o sistema é estável ou não.
Antes de usar , usaremos a função para entrar com no MATLAB. Como o denominador de está fatorizado, precisamos expandi-lo para sabermos como será a entrada de . Por isso, antes de usarmos , vamos multiplicar os termos do denominador de .
Passo 2
Vamos multipicar os termos do denominador de usando o MATLAB. Em um novo script, digite as linhas de código:

Na primeira linha, definimos uma variável simbólica .
Na segunda linha, entramos com o denominador de , que é armazenado em .
Na terceira linha, usamos o comando em para multiplicar os termos de e gerar um polinômio, armazenado em .
Rodando o programa, temos:

Passo 3
Após expandir o denominador de , vamos criar as entradas de , que tem a sintaxe:
A função tem como entrada dois vetores, o primeiro contendo os coeficientes do polinômio do numerador da função de transferência (representado por ) e outro contendo os coeficientes do polinômio do denominador (representado por ). retorna um objeto representando a função de transferência, que será armazenada em .
Para , o polinômio do numerador é . Já o polinômio do denominador é .
Em um novo script ou no mesmo script onde foi calculado, vamos criar as entradas de . Como o polinômio do numerador tem somente um elemento correspondendo a , a variável representando seus coeficientes pode ser um número real. Chamaremos essa variável de e ela é igual a .
A outra variável é um vetor chamado , contendo os coeficientes de , indo do elemento com maior expoente ao de menor expoente:

Logo abaixo das linhas onde as variáveis e foram criadas, já colocamos o comando para criar , que será armazenado em .
Antes de continuar, vamos conferir , pra ver se não digitamos alguma coisa errada. Vamos executar o programa que temos até agora e imprimir no Command Window:

Até aqui, tudo certo, podemos continuar ;D
Passo 4
O próximo passo é plotar o diagrama de Nyquist de . Para isto, use a função , que tem como sintaxe:
Ela tem como entrada uma função de transferência, criada usando o comando do MATLAB (representada por acima), e ela gera um gráfico com o diagrama de Nyquist para .
Adicione em seu código o comando:
![]()
Execute o programa e você terá o diagrama de Nyquist de :
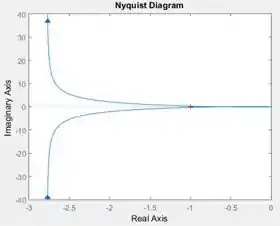
Esse diagrama tá meio esquisitinho, né? Mas não se preocupe, a aplicação do critério de Nyquist nele será exatamente igual como fizemos nos outro diagramas com formatos mais “tradicionais”.
Passo 5
Vamos avaliar a estabilidade do sistema aplicando o critério de Nyquist no diagrama que plotamos no passo anterior. O critério de Nyquist é dado pela equação:
Onde:
- é o número de polos positivos da função de transferência em malha fechada;
- é o número de voltas que o diagrama de Nyquist dá em torno de . é positivo se a volta for no sentido horário. Se for no sentido anti-horário, é negativo.
- é o número de polos positivos da função de transferência em malha aberta.
Pelo critério de Nyquist, para que um sistema seja estável, deve ser igual a .
O é obtido calculando as raízes do denominador da função de transferência em malha aberta, no caso, . Para isto, é mais fácil a gente pegar o dado diretamente no enunciado, onde os termos do denominador não foram multiplicados:
Neste exercício, o denominador de é , que tem como raízes , e . Logo, não tem polos positivos e .
é obtido pelo diagrama de Nyquist. Vamos rever o diagrama de Nyquist gerado no passo anterior:
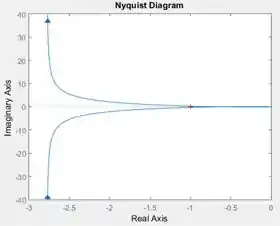
Note que tem uma cruzinha vermelha no meio gráfico, marcando o ponto de coordenadadas . Vamos dar um zoom na região ontem tem a cruzinha, para ver se o diagrama de Nyquist (que é a curva azul com setinhas) não dá alguma volta em torno dela:

Veja que a parte do diagrama de Nyquist (que é a curva azul com setinhas) que parecia uma reta horizontal na verdade é uma voltinha! E essa voltinha não contorna a cruzinha a vermelha, por isso, o diagrama não dá volta alguma em torno de e .
Tendo e , calculamos . Temos que . Como é igual a , o sistema é estável.
Resposta
Sistema estável.