Diagrama de Bode
Teoria
Introdução
E aí, galerinha mais linda do Brasil, tudo joia? Se você está passando por alguma disciplina de Controle ou já passou, já deve ter ouvido falar do diagrama de Bode.
O diagrama de Bode é a representação gráfica da razão de amplitude (RA) entre a resposta e a entrada e do ângulo de fase, que é o ângulo que a resposta avança ou atrasa em relação à entrada. Para relembrarmos direitinho do que se trata, vamos de exemplo. Digamos que você tenha a seguinte função de transferência:
O diagrama de Bode para é:
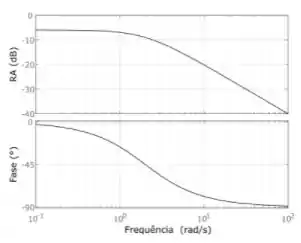
O gráfico acima é a razão de amplitude, em decibéis (dB), e o gráfico abaixo, o ângulo de fase em graus (°). Ambos estão em função da frequência, em rad/s, em uma escala logarítmica.
A partir do diagrama de Bode, podemos tirar algumas informações sobre o sistema dinâmico modelado pela função de transferência, como se o sistema é estável ou não ou qual o máximo valor de ganho que podemos usar de forma que o sistema continue estável (o que chamamos de margem de ganho).
Caso os conceitos de diagrama de Bode não estejam muito frescos na sua memória, não esquente, aqui no Responde Aí, temos uma seção de Sistemas de Controle, que tem um capítulo inteirinho só falando de diagrama de Bode e de como utilizá-lo.
Na aula de hoje, vamos aprender como plotar diagramas de Bode no MATLAB, a fazer uma análise de estabilidade a partir dos diagramas gerados e a obter a margem de ganho. Bora lá?
Plotando um diagrama de Bode no MATLAB
O comando para plotar um diagrama de Bode no MATLAB é bem diretão:
Ele tem como entrada uma função de transferência, criada usando o comando do MATLAB, e ele gera um gráfico com o diagrama de Bode para a .
Vamos ver no MATLAB como fica. Vamos gerar o diagrama de Bode para a função de transferência:
Em um script novo, entre com no MATLAB usando a função , digitando as seguintes linhas de código:
Na primeira linha, criamos uma variável que contém o numerador de .
Na segunda linha, criamos um vetor em que cada elemento é um coeficiente do polinômio do denominador, indo do componente com maior expoente () ao de menor expoente ().
Na terceira linha, usamos a função para criar .
Para plotar o diagrama de Bode de , incluímos no script o comando:
Ao executar o programa, teremos o diagrama de Bode para :
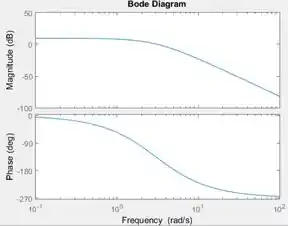
A curva de cima é a curva de razão de amplitude e a curva de baixo, de ângulo de fase. O MATLAB chama a razão de amplitude de .
Bem lindo e prático, né? O mais legal é que existem algumas informações que podemos tirar deste plot.
Estabilidade e diagramas de Bode
A partir do diagrama de Bode, podemos avaliar a estabilidade de um sistema usando o critério de Bode. O critério de Bode diz que um sistema é estável se a razão de amplitude for menor que na frequência em que o ângulo de fase atinge .
Vamos aplicar esse critério no diagrama de Bode de . Para facilitar acharmos o ângulo de fase igual a , recomendo colocar o comando logo abaixo do comando , para o gráfico ter linhas de grade. O código no MATLAB ficaria assim:
Quando executarmos o programa, teremos o diagrama de Bode de com linhas de grade. Ao clicar sobre as curvas azuis dos gráficos, se formará um quadradinho preto dando as informações de frequência, razão de amplitude e ângulo de fase do ponto onde clicamos.
Para avaliar a estabilidade do sistema usando o critério de Bode, clique sobre a curva do ângulo de fase e ache o ponto onde o ângulo é igual a , como na figura abaixo:
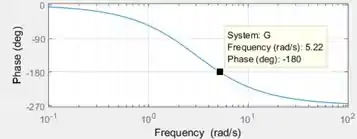
Vemos que, quando o ângulo de fase atinge , a frequência é de .
Agora, veja na curva de razão de amplitude ( no MATLAB) qual é a RA na frequência de , clicando sobre a curva e arrastando o quadradinho preto até encontrar esse valor de frequência, como na figura abaixo:
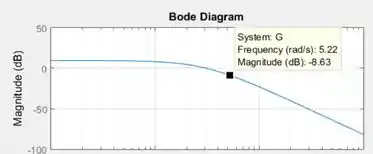
Vemos que a RA é de a uma frequência de . Pelo critério de Bode, o sistema é estável, pois a RA é menor que na frequência onde o ângulo de fase é .
Margem de ganho e margem de fase
Outras informações que podemos extrair do diagrama de Bode, que têm tudo a ver com o critério de Bode, são as margens de ganho e de fase. Essas informações são muito importantes em projetos de controladores, pois ajudam a ver se o sistema está bem projetado e sintonizado.
A margem de ganho é o valor máximo que posso multiplicar o ganho de um sistema, de forma que ela permaneça estável. Se multiplicar o ganho por um valor maior que a margem de ganho, o sistema se torna instável.
A margem de fase define o quanto de atraso a malha ainda suporta antes de se tornar instável.
Em um sistema estável, ambas as margens são positivas.
Isso foi um brevíssimo resumo desses conceitos. Você pode vê-los com muito mais detalhe aqui no Responde Aí, no capítulo de Resposta em Frequência.
No MATLAB, encontramos as margens de ganho e de fase por meio do comando:
A função tem como entrada uma função de transferência criada usando o comando e ela gera, ao executarmos o programa, um gráfico com o diagrama de Bode de com indicações das margens de ganho e de fase.
Para exemplificar, vamos calcular a margem de ganho e a margem de fase do exemplo usado na seção acima. No script onde você entrou , substitua o comando por e apague o . Seu programa agora tem essa cara:
Vamos rodar e ver o que acontece?
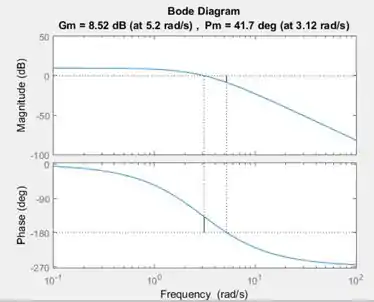
Voilà! O MATLAB nos dá o diagrama de Bode já com as margens de ganho e de fase. As margens são dadas no título do gráfico e são representadas pelas linhas verticais cheias. As linhas verticais pontilhadas indicam a frequência onde as margens foram medidas.
O MATLAB nos informa que a margem de ganho é em . Como a margem de ganho é positiva, o sistema é estável. Já o ganho de fase é de em . Novamente, como a margem é positiva, o sistema é estável.
O interessante é que as linhas tracejadas no gráfico indicam bem como as margens são encontradas em um diagrama de Bode.
Em um diagrama de Bode, a margem de ganho é calculada encontrando a frequência onde o ângulo de fase é e fazendo a diferença entre e a RA nessa mesma frequência. Já a margem de fase é calculada encontrando a frequência onde a RA é e fazendo a diferença entre o ângulo de fase nessa frequência e .
No gráfico acima, uma linha pontilhada horizontal passa por (no gráfico de ) e outra passa por (no gráfico de ).
Além disso, no mesmo gráfico acima, note que a linha pontilhada vertical indicando a frequência da margem de ganho passa bem em cima do ponto onde o ângulo de fase é . Já a linha pontilhada vertical indicando a frequência da margem de fase passa bem em cima do ponto onde a RA é .
E aí, curtiu a aula? Agora é praticar pra fixar bem o conteúdo ;)
Plotando um diagrama de Bode no MATLAB
Estabilidade e diagramas de Bode
Margem de ganho e margem de fase
Exercícios Resolvidos
Exercício Resolvido #1
“Adaptado de UFRGS – Departamento de Engenharia Elétrica – ENG04450 – Sistemas de Controle: Laboratório I – Introdução ao MATLAB. Profs. João Manoel Gomes da Silva e Romeu Reginatto (2002)”
Usando o MATLAB, construa o diagrama de Bode da função de transferência:
Passo 1
O exercício pede para plotarmos o diagrama de Bode de usando o MATLAB. Para isto, devemos primeiro entrar com no MATLAB usando a função . Em seguida, usaremos a função para plotar o diagrama de Bode.
Passo 2
O primeiro passo para resolver o exercício é entrar com no MATLAB. Para isto, usaremos a função , que cria funções de transferência e tem a seguinte sintaxe:
A função tem como entrada dois vetores, o primeiro contendo os coeficientes do polinômio do numerador da função de transferência (representado por ) e outro contendo os coeficientes do polinômio do denominador (representado por ). retorna um objeto representando a função de transferência, que será armazenada em .
Para , o polinômio do numerador é . Já o polinômio do denominador é .
Em um novo script, vamos criar duas variáveis representando os coeficientes dos polinômios, para servirem de entrada para . Como o polinômio do numerador tem somente um elemento correspondendo a , a variável representando seus coeficientes pode ser um número real. Chamaremos essa variável de e ela é igual a .
A outra variável é um vetor chamado , contendo os coeficientes de , indo do elemento com maior expoente ao de menor expoente:
Em seguida, adicione o comando abaixo para criar :
A função de transferência é armazenada na variável . Você pode ver como ficou ao rodar o programa e pedir ao MATLAB para imprimir no Command Window:
Igualzinho ao enunciado ;)
Passo 3
Tendo entrado com no MATLAB, podemos plotar seu diagrama de Bode, usando o comando , que tem a sintaxe:
Ele tem como entrada uma função de transferência (representada pela variável ), criada usando o comando do MATLAB, e ele gera um gráfico com o diagrama de Bode para .
No script criado no passo 2, adicione a seguinte linha de código:
Se quiser, digite logo abaixo de o comando , para que o diagrama de Bode tenha linhas de grade.
Ao rodar seu programa, você terá o diagrama de Bode de .
Resposta
Exercício Resolvido #2
“Adaptado de Seborg, Process Dynamics and Control, 4ª ed.: Wiley, 2016, p. 34, Exercício 14.7”
No MATLAB, esboce o diagrama de Bode para a função de transferência de um sistema em malha aberta mostrada abaixo e determine sua estabilidade em malha fechada.
Passo 1
O exercício pede para plotarmos o diagrama de Bode de e avaliarmos a estabilidade de , a partir do diagrama plotado. Logo, para ver se é estável ou não, usaremos o critério de Bode.
Para fazer nosso programa, executaremos os seguintes passos: devemos primeiro entrar com no MATLAB usando a função . Em seguida, usaremos a função para plotar o diagrama de Bode de . Avaliaremos a estabilidade de usando o gráfico gerado por nosso programa, a partir do critério de Bode.
Passo 2
O primeiro passo para resolver o exercício é entrar com no MATLAB. Para isto, usaremos a função , que cria funções de transferência e tem a seguinte sintaxe:
A função tem como entrada dois vetores, o primeiro contendo os coeficientes do polinômio do numerador da função de transferência (representado por ) e outro contendo os coeficientes do polinômio do denominador (representado por ). retorna um objeto representando a função de transferência, que será armazenada em .
Para , o polinômio do numerador é . Já o polinômio do denominador é .
Em um novo script, vamos criar duas variáveis representando os coeficientes dos polinômios, para servirem de entrada para . Como o polinômio do numerador tem somente um elemento correspondendo a , a variável representando seus coeficientes pode ser um número real. Chamaremos essa variável de e ela é igual a .
A outra variável é um vetor chamado , contendo os coeficientes de , indo do elemento com maior expoente ao de menor expoente:
Incluímos logo abaixo o comando , para criar e armazená-la na variável .
Se quiser conferir se digitou tudo certinho, você pode rodar o programa que tem até agora e pedir ao MATLB para imprimir no Command Window e compará-lo com o do enunciado:
Se tiver entrado com tudo certinho, vai sair igualzinho a .
Passo 3
Tendo entrado com no MATLAB, vamos plotar o diagrama de Bode, usando o comando , que tem a sintaxe:
Ele tem como entrada uma função de transferência (representada pela variável ), criada usando o comando do MATLAB, e ele gera um gráfico com o diagrama de Bode para .
No script criado no passo 2, adicione as seguintes linhas de código:
Além do comando para plotar o diagrama de Bode de , incluímos o comando , para que o diagrama tenha linhas de grade. As linhas de grade vão ajudar a avaliar a estabilidade de pelo critério de Bode, como veremos mais pra frente.
Vamos rodar o programa para vermos o diagrama de Bode de :
O gráfico de cima, de pela frequência, representa a razão de amplitude e o gráfico de baixo, de pela frequência, o ângulo de fase.
Passo 4
Usamos o critério de Bode para ver se é estável ou não no diagrama de Bode. O critério de Bode diz que um sistema é estável se a razão de amplitude for menor que na frequência em que o ângulo de fase atinge .
No diagrama de Bode gerado pelo MATLAB, avaliaremos a razão de amplitude no gráfico de pela frequência e o ângulo de fase no gráfico de pela frequência.
O primeiro passo, então, é achar a frequência em que o ângulo de fase é . Para isto, clique sobre a curva do gráfico de baixo, cujo eixo vertical é . Aparecerá um quadradinho preto que informa a frequência e o ângulo de fase do ponto sobre o qual você clicou. Arraste o quadradinho até que seja igual a . Use as linhas de grade para se orientar. Ao fazer isso, você terá algo parecido com a imagem abaixo:
Vemos que a frequência em que o ângulo de fase é é de .
Passo 5
Sabendo que o ângulo de fase atinge em uma frequência de , vamos procurar no gráfico de cima do diagrama de Bode gerado pelo MATLAB, isto é, no gráfico cujo eixo vertical é , qual é a razão de amplitude em .
Para isto, clique sobre a curva do gráfico , para aparecer aquele quadradinho preto com as informações sobre o ponto onde você clicou. Dessa vez, ele informará a frequência e a razão de amplitude do ponto. Arraste o quadradinho preto até atingir uma frequência de , usando as linhas de grade para se guiar. Ao fazer isso, seu gráfico de ficará com essa cara:
Vemos que a razão de amplitude em é , menor que . Logo, é estável.
Resposta
Sistema estável
Exercício Resolvido #3
“Adaptado de UnB – 107506: Laboratório de Controle de Processos. Aula: MATLAB. Prof. Eduardo Stockler Tognetti (2018) – Exercício 4”
Seja
Plote o diagrama de Bode e encontre as margens de fase e de ganho de .
Passo 1
O exercício pede para plotarmos o diagrama de Bode de e encontarmos as margens de fase e de ganho de . Para isto, primeiramente vamos entrar com no MATLAB usando a função . Em seguida, usaremos a função , que plota o diagrama de Bode já informando as margens de fase e de ganho.
Passo 2
O primeiro passo para resolver o exercício é entrar com no MATLAB. Para isto, usaremos a função , que cria funções de transferência e tem a seguinte sintaxe:
A função tem como entrada dois vetores, o primeiro contendo os coeficientes do polinômio do numerador da função de transferência (representado por ) e outro contendo os coeficientes do polinômio do denominador (representado por ). retorna um objeto representando a função de transferência, que será armazenada em .
Para , o polinômio do numerador é . Já o polinômio do denominador é .
Em um novo script, vamos criar duas variáveis representando os coeficientes dos polinômios, para servirem de entrada para . Como o polinômio do numerador tem somente um elemento correspondendo a , a variável representando seus coeficientes pode ser um número real. Chamaremos essa variável de e ela é igual a .
A outra variável é um vetor chamado , contendo os coeficientes de , indo do elemento com maior expoente ao de menor expoente:
Logo abaixo, já adicionamos o comando , para criar a função de transferência e armazená-la na variável .
Se quiser, você pode rodar o programa que você tem até agora, só pra conferir se você entrou certo com . Para isto, imprima no Command Window:
Se estiver igualzinho a apresentado no enunciado, pode partir para o próximo passo :)
Passo 3
Após entrar com , podemos usar o comando para plotar o diagrama de Bode de já com as margens de ganho e de fase destacadas. A função tem a seguinte sintaxe:
Ela tem como entrada uma função de transferência criada usando o comando (representada por ) e ela gera, ao executarmos o programa, um gráfico com o diagrama de Bode de , informando já no título do gráfico as margens de ganho e de fase e a frequência na qual elas foram calculadas.
Para chegarmos no resultado do exercício, adicione ao seu código o comando:
Com este comando, geraremos o diagrama de Bode de e obteremos as margens de fase e de ganho.
Rode o programa para ver o resultado:
No título do gráfico, a margem de ganho é indicada por e margem de fase, por . Temos que a margem de ganho é e a margem de fase, .
Resposta
A margem de ganho de é e a margem de fase, .
Exercício Resolvido #4
“Adaptado de Seborg, Process Dynamics and Control, 4ª ed.: Wiley, 2016, p. 34, Exercício 14.5”
Usando o MATLAB, determine se o seguinte processo pode ser tornado instável aumentando-se o ganho dele. Utilize argumentos baseados em resposta em frequência e critério de Bode.
Passo 1
Quando o exercício pede para determinarmos se pode se tornar instável aumentando o ganho, na real ele está nos pedindo para ver se já é estável, com outras palavras. Se ele for estável na forma que foi apresentado no enunciado, avaliando-o pelo critério de Bode, significa que tem espaço para aumentar o ganho até que o processo se torne instável.
Logo, o exercício pede para vermos se é estável ou não, nos baseando em resposta em frequência e critério de Bode. Para isto, plotaremos o diagrama de Bode de usando o MATLAB.
No nosso programa, devemos primeiro entrar com no MATLAB usando a função . Em seguida, usaremos a função para plotar o diagrama de Bode. Avaliaremos a estabilidade de usando o gráfico gerado por nosso programa, a partir do critério de Bode.
Passo 2
O primeiro passo para resolver o exercício é entrar com no MATLAB. Para isto, usaremos a função , que cria funções de transferência e tem a seguinte sintaxe:
A função tem como entrada dois vetores, o primeiro contendo os coeficientes do polinômio do numerador da função de transferência (representado por ) e outro contendo os coeficientes do polinômio do denominador (representado por ). retorna um objeto representando a função de transferência, que será armazenada em .
Para , o polinômio do numerador é . Já o polinômio do denominador é .
Em um novo script, vamos criar duas variáveis representando os coeficientes dos polinômios, para servirem de entrada para . Como o polinômio do numerador tem somente um elemento correspondendo a , a variável representando seus coeficientes pode ser um número real. Chamaremos essa variável de e ela é igual a .
A outra variável é um vetor chamado , contendo os coeficientes de , indo do elemento com maior expoente ao de menor expoente:
Em seguida, adicione o comando abaixo para criar :
A função de transferência é armazenada na variável . Você pode ver como ficou ao rodar o programa e pedir ao MATLAB para imprimir no Command Window:
Passo 3
Tendo entrado com no MATLAB, podemos plotar seu diagrama de Bode, usando o comando , que tem a sintaxe:
Ele tem como entrada uma função de transferência (representada pela variável ), criada usando o comando do MATLAB, e ele gera um gráfico com o diagrama de Bode para .
No script criado no passo 2, adicione as seguintes linhas de código:
Além do comando para plotar o diagrama de Bode de , incluímos o comando , para que o diagrama tenha linhas de grade. As linhas de grade vão ajudar a avaliar a estabilidade de pelo critério de Bode.
Vamos rodar o programa para vermos o diagrama de Bode de :
Passo 4
Com o diagrama de Bode em mãos, podemos usar o critério de Bode para ver se é estável ou não. O critério de Bode diz que um sistema é estável se a razão de amplitude for menor que na frequência em que o ângulo de fase atinge .
Lembrando que no diagrama de Bode gerado pelo MATLAB, a razão de amplitude é chamada de .
O primeiro passo, então, é achar a frequência em que o ângulo de fase é . Para isto, clique sobre a curva do gráfico de baixo, cujo eixo vertical é . Aparecerá um quadradinho preto que informa a frequência e o ângulo de fase do ponto sobre o qual você clicou.
Arraste o quadradinho até que seja igual a . Use as linhas de grade para te orientar. Ao fazer isso, você terá algo parecido com a imagem abaixo:
Vemos que a frequência em que o ângulo de fase é é de .
Passo 5
Sabendo que o ângulo de fase atinge em uma frequência de , vamos procurar no gráfico de cima do diagrama de Bode gerado pelo MATLAB, isto é, no gráfico cujo eixo vertical é , qual é a razão de amplitude em .
Para isto, clique sobre a curva do gráfico , para aparecer aquele quadradinho preto com as informações sobre o ponto onde você clicou. Dessa vez, ele informará a frequência e a razão de amplitude do ponto.
Arraste o quadradinho preto até atingir uma frequência de , usando as linhas de grade para se guiar. Ao fazer isso, seu gráfico de ficará com essa cara:
Vemos que a razão de amplitude em é , menor que . Logo, é estável.
Em outras palavras, podemos aumentar o ganho de até que o sistema se torne instável, pois podemos aumentar o ganho até que a razão de amplitude se torne maior que , partindo de no estado atual, onde a razão de amplitude é de na frequência em que o ângulo de fase é , atendendo ao critério de Bode.
Em outras palavras, temos uma “folga” de .
Resposta
É possível que o processo se torne instável aumentando-se o ganho, pois podemos aumentar o ganho até que a razão de amplitude se torne maior que na frequência em que o ângulo de fase atinge , visto que apresenta razão de amplitude negativa nessa frequência.
Exercício Resolvido #5
“Adaptado de Norman N. Nise, Engenharia de sistemas de controle, 6ª ed., Rio de Janeiro, 2012. Exercício 10.13”
Usando o MATLAB, obtenha a margem de ganho, margem de fase, a frequência de e a frequência de para um sistema com realimentação unitária e função de transferência em malha aberta:
Passo 1
Para , o exercício pede para encontrarmos:
- Margem de ganho;
- Margem de fase;
- Frequência de ;
- Frequência de .
Obtemos tudo isso usando o comando do MATLAB.
No nosso programa, primeiramente vamos entrar com no MATLAB usando a função . Em seguida, usaremos a função , que plota o diagrama de Bode já informando as margens de fase e de ganho e as frequências de e .
Passo 2
Vamos entrar com no MATLAB. Para isto, usaremos a função , que cria funções de transferência e tem a seguinte sintaxe:
A função tem como entrada dois vetores, o primeiro contendo os coeficientes do polinômio do numerador da função de transferência (representado por ) e outro contendo os coeficientes do polinômio do denominador (representado por ). retorna um objeto representando a função de transferência, que será armazenada em .
Para , o polinômio do numerador é . Já o polinômio do denominador é .
Em um novo script, vamos criar duas variáveis representando os coeficientes dos polinômios, para servirem de entrada para . Como o polinômio do numerador tem somente um elemento correspondendo a , a variável representando seus coeficientes pode ser um número real. Chamaremos essa variável de e ela é igual a .
A outra variável é um vetor chamado , contendo os coeficientes de , indo do elemento com maior expoente ao de menor expoente:
Logo abaixo, já digitamos o comando , para criar e armazená-la na variável . Se quiser, você pode rodar o programa que você tem até agora para conferir se você entrou certo com . Para isto, imprima no Command Window:
Se estiver igualzinho a , pode prosseguir :)
Passo 3
Após entrar com , usamos o comando , que plota o diagrama de Bode de já com as margens de ganho e de fase destacadas. A função tem a seguinte sintaxe:
Ela tem como entrada uma função de transferência criada usando o comando (representada por ) e ela gera, ao executarmos o programa, um gráfico com o diagrama de Bode de , informando já no título do gráfico as margens de ganho e de fase e a frequência na qual elas foram calculadas.
Para chegarmos no resultado do exercício, adicione ao seu código o comando:
Com este comando, geraremos o diagrama de Bode de e obteremos as margens de fase e de ganho. Rodando o programa para ver o resultado, temos:
No título do gráfico, a margem de ganho é indicada por e margem de fase, por . Temos que a margem de ganho é e a margem de fase, .
Com isso, já temos as margens de ganho e de fase pedidas pelo enunciado. Mas e as frequências de e ?
Passo 4
Para encontrarmos as frequências, vamos relembrar como se calculam as margens de ganho e de fase usando o diagrama de Bode.
Em um diagrama de Bode, a margem de ganho é calculada encontrando a frequência onde o ângulo de fase é e fazendo a diferença entre e a razão de amplitude (no caso do gráfico gerado pelo MATLAB, ) nessa mesma frequência. Em outras palavras, isso quer dizer que a frequência onde a margem de ganho é calculada é a frequência de .
Repare que o título do gráfico diz: , informando que a margem de ganho de foi calculada em . Isso quer dizer a frequência de é .
Outra alternativa para encontrar a frequência de é clicar no gráfico de baixo, o de , e arrastar o quadradinho preto até encontrar o dado igual a , como na imagem abaixo:
Veja que a frequência desse ponto é igual a , praticamente igual ao valor dado pelo título do gráfico. Repare também que o ponto onde é igual a está exatamente sobre a linha vertical pontilhada que indica a posição da margem de ganho no diagrama de Bode. Isso porque a margem de ganho foi determinada como eu disse acima.
Passo 5
Para encontrar a frequência de , vamos relembrar como se calcula a margem de fase usando o diagrama de Bode. Ela é calculada encontrando a frequência onde a razão de amplitude (no diagrama gerado pelo MATLAB, ) é e fazendo a diferença entre o ângulo de fase nessa frequência e .
Em outras palavras, isso quer dizer que a frequência onde a margem de fase é calculada é a frequência de .
Repare que o título do gráfico diz: , informando que a margem de fase de foi calculada em . Isso quer dizer a frequência de é .
Outra alternativa para encontrar a frequência de é clicar no gráfico de cima, o de , e arrastar o quadradinho preto até encontrar o dado o mais próximo possível de , como na imagem abaixo (é difícil achar exatamente o ):
Veja que a frequência desse ponto é igual a , dando uma razão de amplitude de , bem próxima de . Repare que a frequência é bem próxima da dada no título do gráfico para a margem de fase.
Como é difícil acertar o ponto de , recomendo pegar os valores dados pelo título do gráfico.
Resposta
- Margem de ganho:
- Margem de fase:
- Frequência de :
- Frequência de :
Exercício Resolvido #6
“UnB – 107506: Laboratório de Controle de Processos. Aula: MATLAB. Prof. Eduardo Stockler Tognetti (2018) – Exercício 4”
Seja
Plote o diagrama de Bode e encontre as margens de fase e de ganho de .
Passo 1
O exercício pede para plotarmos o diagrama de Bode de e para encontrarmos a margem de ganho e a margem de fase de . Faremos tudo isso com um único comando do MATLAB: .
No nosso programa, primeiramente vamos entrar com usando a função . Em seguida, usaremos a função , que plota o diagrama de Bode já informando as margens de fase e de ganho.
Passo 2
Use a função para criar a função de transferência . Lembrando que tem a sintaxe:
A função tem como entrada dois vetores, o primeiro contendo os coeficientes do polinômio do numerador da função de transferência (representado por ) e outro contendo os coeficientes do polinômio do denominador (representado por ). retorna um objeto representando a função de transferência, que será armazenada em .
Em um novo script, vamos criar dois vetores contendo os coeficientes dos polinômios, para servirem de entrada para . O primeiro vetor se chamará e terá os coeficientes do numerador de . Já o segundo vetor se chamará e conterá os coeficientes do denominador de .
O polinômio do numerador é e o do denominador, . Por isso, e ficarão assim:
Logo abaixo, já inserimos o comando , para criar e armazená-la na variável .
Vamos rodar o programa digitado até agora para conferir se está tudo certo com , imprimindo no Command Window:
Tá igualzinho ao enunciado, bora plotar esse diagrama de Bode!
Passo 3
Para plotar o diagrama de Bode de , usaremos o comando , que além de gerar o diagrama, ainda dá pra gente as margens de ganho e de fase. A função tem a seguinte sintaxe:
Ela tem como entrada uma função de transferência criada usando o comando (representada por ) e ela gera, ao executarmos o programa, um gráfico com o diagrama de Bode de , informando já no título do gráfico as margens de ganho e de fase.
Para chegarmos na solução do exercício, adicione ao seu código o comando:
Rode o programa para ver o resultado, temos:
No título do gráfico, a margem de ganho é indicada por e margem de fase, por . Temos que a margem de ganho é e a margem de fase, .
Uma margem de ganho infinita indica que o sistema é sempre estável, independente do valor do ganho que eu usar no controle do sistema.
Resposta
Margem de ganho:
Margem de fase:
Exercício Resolvido #7
“UnB – 107506: Laboratório de Controle de Processos. Aula: MATLAB. Prof. Eduardo Stockler Tognetti (2018) – Exercício 4”
Seja
Plote o diagrama de Bode e encontre as margens de fase e de ganho de .
Passo 1
O exercício pede para plotarmos o diagrama de Bode de e para encontrarmos a margem de ganho e a margem de fase de . Obteremos a solução do exercício com um único comando do MATLAB: .
No nosso programa, precisamos entrar com usando a função . Contudo, antes de aplicar , precisamos multiplicar os termos do numerador e do denominador de , para obtermos os polinômios cujos coeficientes servirão de entrada para .
Tendo entrado com , ela servirá de entrada para a função , que plota o diagrama de Bode já informando as margens de fase e de ganho.
Passo 2
Vamos multiplicar os termos do numerador e do denominador no próprio MATLAB mesmo, começando pelo numerador. Em um novo script, digite as seguintes linhas de código:
Na primeira linha, é definida uma variável simbólica .
Na segunda linha, criamos uma variável que armazena o numerador de no formato atual.
Na terceira linha, usamos o comando para multiplicar os termos de e gerarmos o polinômio do numerador, que é armazenado em .
Execute o programa e imprima no Command Window :
Logo, o polinômio do numerador de é .
Faça a mesma coisa para o denominador de , digitando no mesmo script as linhas de código:
Primeiramente, criamos a variável para armazenar o denominador de no formato que ele está no enunciado. Em seguida, usamos nele para gerar o polinômio do denominador, que é armazenado em . O polinômio do denominador será:
Logo, .
Passo 3
Tendo os polinômios do numerador e do denominador de , podemos usar a função para criar . Lembrando que tem a sintaxe:
A função tem como entrada dois vetores, o primeiro contendo os coeficientes do polinômio do numerador da função de transferência (representado por ) e outro contendo os coeficientes do polinômio do denominador (representado por ). retorna um objeto representando a função de transferência, que será armazenada em .
Em um novo script ou no mesmo onde você obteve os polinômios, crie dois vetores contendo os coeficientes dos polinômios, para servirem de entrada para . O primeiro vetor se chamará e terá os coeficientes do numerador de . Já o segundo vetor se chamará e conterá os coeficientes do denominador de .
O polinômio do numerador é e o do denominador, , logo, e ficarão assim:
Já podemos pôr logo abaixo o comando , para criar a variável , que contém .
Vamos rodar o programa digitado até agora para conferir se está tudo certo com , imprimindo no Command Window:
Está tudo certo, já podemos plotar o diagrama de Bode a partir de .
Passo 4
Plotaremos o diagrama de Bode de com o comando , que além de nos dar diagrama, ainda informa pra gente as margens de ganho e de fase. O comando tem a como sintaxe:
Ele tem como entrada uma função de transferência criada usando o comando (representada por ) e ele gera, ao executarmos o programa, um gráfico com o diagrama de Bode de , informando no título do gráfico as margens de ganho e de fase.
Para chegarmos na solução do exercício, adicione ao seu código o comando:
Execute o programa para obter a solução do exercício:
No título do gráfico, a margem de ganho é indicada por e a margem de fase, por . Temos que ambas as margens são infinitas. Mas por quê?
Note no diagrama de que a curva de a razão de amplitude está inteira abaixo de , isto é, não importa a frequência, a razão de amplitude sempre será menor do que . Isso indica que o sistema é sempre estável, isto é, podemos multiplicar o ganho por qualquer valor que o sistema permanecerá estável. Por isso a margem de ganho é infinita.
Uma margem de fase infinita indica que a malha suporta qualquer valor de atraso, pois ela permanecerá estável.
Resposta
Margem de ganho:
Margem de fase:
Exercício Resolvido #8
“Adaptado de “An Engineer’s Guide to MATLAB: With Applications from Mechanical, Aerospace, Electrical, Civil, and Biological Systems Engineering” (3ª edição), escrito por Edward B. Magrab et al. Exercício 10.2, p. 606”
O sistema de suspensão mostrado abaixo tem o nível da superfície da estrada como entrada e a posição absoluta como saída.
A função de transferência do sistema é:
Dependendo do uso, a massa do carro pode dobrar. Gere em um mesmo gráfico o diagrama de Bode para . Assuma que , , e .
Passo 1
Neste exercício, plotaremos o diagrama de Bode de para valores diferentes de , sendo que os diagramas deverão estar em um mesmo gráfico, para facilitar a comparação. Para fazermos isso, a função para criar e o comando para plotar o diagrama ficarão dentro de um laço , que atualizará e o diagrama para cada valor de .
Passo 2
O primeiro passo é entrar com os dados de massa, rigidez e amortecimento do enunciado. Em um script novo, entre com os valores de , , e :
Abaixo dos dados que você acabou de digitar, inicie um laço , com variável de controle , representando a massa do carro. Essa variável de controle deve ir de a , pois o enunciado pede para vermos o diagrama de Bode de para :
O passo da faixa de valores de você pode escolher o que quiser. Eu escolhi , de forma que em assumirá três valores distintos: , e . Isto fará que o meu gráfico com os diagramas de Bode no final tenha três curvas, uma para cada valor de .
Passo 3
Vamos entrar com dentro do laço , escrevendo dentro dele o comando , que tem como sintaxe:
A função tem como entrada dois vetores, o primeiro contendo os coeficientes do polinômio do numerador da função de transferência (representado por ) e outro contendo os coeficientes do polinômio do denominador (representado por ). retorna um objeto representando a função de transferência, que será armazenada em .
Vamos criar dois vetores, dentro do laço , contendo os coeficientes dos polinômios do numerador e do denominador de . O polinômio do numerador é e seus coeficientes serão armazenados em um vetor chamado . Já o polinômio do denominador é:
Seus coeficientes serão armazenados em um vetor chamado . Desta forma, o laço tem essa cara por enquanto:
Logo abaixo dos vetores, já podemos incluir o comando , para criar a variável , que contém .
Com o laço de repetição , os vetores e serão atualizados a cada iteração, com um valor de diferente, gerando, portanto, uma função de transferência diferente.
Passo 4
Para gerar o diagrama de Bode para cada função de transferência diferente, utilize dentro do laço o comando , que tem a sintaxe:
Ele tem como entrada uma função de transferência (representada pela variável ), criada usando o comando , e ele gera um gráfico com o diagrama de Bode para .
Logo, acrescente o comando dentro do laço :
Abaixo de , inclua o comando . Este comando serve para que o gráfico com o diagrama de Bode seja atualizado a cada iteração, mas sem que as curvas da iteração anterior desapareçam.
Pra finalizar, coloque logo abaixo do laço o comando:
Ele fará com que o gráfico com os diagramas de Bode tenham uma legenda, indicando qual curva representa o resultado para determinada massa. As legendas dentro de devem estar na ordem com que os diagramas foram criados.
Resposta
As curvas azuis são o diagrama de Bode para
As curvas vermelhas são o diagrama de Bode para
As curvas amarelas são o diagrama de Bode para