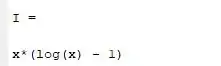Teoria
Alguns conceitos introdutórios
Bem, primeiramente devo te informar que o Matlab adooora trabalhar com matrizes.
Então, uma variável no matlab se comporta como um elemento de uma matriz, mesmo que seja um valor simples como .
Talvez na sua cabeça tá passando algo do tipo, “Mas beleza... e qual é a importância de eu saber disso?”

E para te mostrar isso vamos fazer um exemplo:
Abrindo o Matlab, escreva as seguintes expressões:
Agora dá um Enter! Se você digitou tudo certinho deve aparecer algo assim na sua workspace: (Lembrando que o “;” faz com que a variável não apareça no command window)

Se você der dois cliques em cada variável vai aparecer uma aba como a mostrada acima, revelando que o número na verdade é o elemento da linha 1 e coluna 1 de uma certa matriz chamada , entende?
É o seguinte, uma variável no Matlab é uma região de memória que contém uma matriz, conhecida por um nome especificado pelo usuário. As variáveis do Matlab que armazenam valores escalares, como as do nosso exemplo, são matrizes com uma linha e uma coluna como veremos em tópicos seguintes.
Então no Matlab você está sempre trabalhando com matrizes e essa é uma das justificativas do porquê no Matlab algumas coisas ficam mais simples de trabalhar quando comparadas com outras linguagens semelhantes.
Logo, uma declaração de uma variável no matlab é dada da seguinte forma, primeiro você declara o nome que a variável vai receber e então associa esse nome a algo utilizando o comando “”, logo a forma geral de uma variável é:
![]()
E antes que eu me esqueça o nome da variável no Matlab obrigatoriamente tem que começar por uma letra e não pode ter espaçamento ou caracteres especiais, ok?
Então nada de colocar como variável , que não vai funcionar!
Tipos de Variáveis
Nós ficamos falando sobre anexar algo a essas variáveis e a todo momento estávamos utilizando números, mas será que é só isso mesmo?

Na verdade, não! No Matlab podemos criar diversos tipos de variáveis e a classe dessas variáveis depende unicamente do que estamos associando a elas, logo existe uma infinidade delas. Porém nesse começo utilizamos apenas algumas e são elas que vou te apresentar agora!
Tipo 1: Inteiras e Flutuantes.
Uma variável inteira é representada por um número inteiro, enquanto um flutuante se trata de um número decimal.
Em outras linguagens de programação, esses dois tipos possuem certas diferenças, porém no Matlab as coisas são tratadas de forma mais simples!
Aqui, ambos podem ser declarados da mesma forma que declaramos ali em cima. Vamos escrever algumas constantes bastantes utilizadas na engenharia como: e , que se caracterizam como pontos flutuantes.
Só precisa tomar cuidado com um detalhe: no Matlab, usamos ponto em vez de vírgula! Escrevendo uma de cada vez você deve obter algo assim:
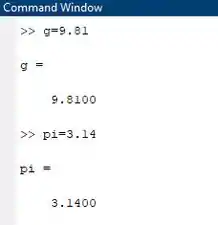
Ou seja, do ponto de vista prático, a forma de criar variáveis inteiras e flutuantes não tem diferença alguma no Matlab.
Além disso bastante cuidado, para o Matlab variáveis do tipo e ainda continuam sendo variáveis do tipo inteira pois quando são inseridas no Matlab, a workspace os armazena como variáveis inteiras. (Deixei esse teste para você fazer, vá no command window e digite e veja o que acontece)
Tipo 2: Strings
Strings são cadeias de caracteres, são variáveis de texto. No Matlab, podem ser inscritos de uma forma bem simples também. Você apenas precisa colocar a informação entre aspas, por exemplo: .

Aqui está provado que segundo o Matlab o melhor curso de Matlab é o do Responde Aí hahaha
Bem, agora que vimos como criar uma variável do tipo string, você precisa saber de um detalhe: o Matlab não entende muito bem alguns caracteres como o “ç”, então é bom tomar cuidado ao usar.
Tipo 3: Variáveis Lógicas
Esse tipo de variável especifica um valor lógico de “verdadeiro” ou “falso”. Isso é representado no Matlab como:
Essas variáveis serão bastantes úteis no estudo de operações lógicas que veremos futuramente.
Tipo 4: Variáveis Simbólicas
Uma variável simbólica na verdade é uma classe de variáveis que existem em softwares destinados a programação numérica. Essas variáveis servem para podermos usar alguns comandos já prontos dentro do Matlab.
Imagina só, você aí pagando cálculo 2 e surge aquela integral cavernosa que tu fica horas e não consegue resolver.... pois bem, SEUS PROBLEMAS ACABARAM!!!

Isso mesmo!!! O Matlab também resolve essas integrais, derivadas, gradientes e várias outras coisas. Esses pacotes são chamados de pacotes simbólicos e é para isso que serve a variável simbólica.
Ok, ok, mas como declarar né? Simples, antes de começar a escrever qualquer coisa insira a palavra no Matlab e vá escrevendo todas as variáveis que são simbólicas separadas por um espaçamento simples e depois aperte Enter, após isso as variáveis que você escreveu se tornam simbólicas.
Para clarear as ideias vamos para um exemplo, vamos escrever a função:
Basta você escrever dessa forma:
Se você escrever certinho vai aparecer isso para você.

Beleza, mas para que isso serve? Vou te dar um spoiler. Escreva no command window, , vai aparecer sabe o que? Isso mesmo a integral analítica da sua função! Vlllllllllllws
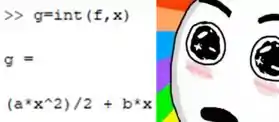
Em outro momento a gente vê todas as coisas que podemos fazer com as variáveis simbólicas, por hoje guarda só como que declaramos.
Encerramos por aqui, aproveita pra dar uma conferida que escolhi especialmente pra você praticar isso tudo.
Bons estudos! 😊
Tipos de Variáveis
Tipo 1: Inteiras e Flutuantes.
Tipo 2: Strings
Tipo 3: Variáveis Lógicas
Tipo 4: Variáveis Simbólicas
Exercícios Resolvidos
Exercício Resolvido #1
Fonte do Exercício. “Elaboração Própria”
- Quais das seguintes constantes não são aceitáveis no Matlab?
a)3.1416b) 23,0c) +10d) 1.0
e)104f) 4E2g) 6h) 3.4E-06
i) 1922j) 1.0Ek) 1,6l) -106.688
Passo 1
Esse é um exercício de aplicação da teoria, ou seja, precisamos apenas verificar cada alternativa e analisar se possui algum erro que a impeça de ser implementada no Matlab.
Então vamos láaaaaaaa
Passo 2
Primeiramente vamos analisar as variáveis do tipo inteiras, ou seja, as variáveis que são compostas apenas por números inteiros.
Olhando as alternativas conseguimos perceber que as únicas variáveis inteiras são:
b) 23,0
d) 1.0
c) +10
e)104
g) 6
i) 1922
Para verificar o erro precisamos apenas lembrar das regras para inserir uma variável inteira no Matlab.
A primeira é que não podem existir caracteres especiais e todas elas passaram nesse critério.
O segundo ponto é sobre a questão do uso da vírgula, no Matlab utilizamos a língua inglesa, ou seja, qualquer casa decimal precisa ser inserida após ponto e não vírgula. Por exemplo, o número 2,6 é 2.6 no Matlab.
Sendo assim, a alternativa b está incorreta.
Portanto as alternativas corretas são:
d) 1.0
c) +10
e)104
g) 6
i) 1922
Passo 3
Agora iremos comentar sobre as variáveis que estão escritas na base E. Para escrever alguma variável no Matlab na base exponencial precisamos apenas colocar a letra E que é similar a base 10 como mostramos abaixo.
Do lado esquerdo da letra E nós temos a parte numérica que corresponde a um valor qualquer.
Já do lado direto da letra E temos o expoente, ou seja, quantas vezes vamos multiplicar o lado esquerdo por 10 até adquirir o valor correspondente.
Esse tipo de notação no ensino médio recebe o nome de notação científica.
Sendo assim, expandindo as alternativas temos:
f)
h) 3.4E-06
Então analisando cada variável escrita na base E, podemos perceber que a única que não está escrita sob essa forma é a alternativa j), pois não é indicado o expoente da base 10, à direita do E.
Passo 4
E finalmente vamos analisar o último tipo de variável que são as do tipo flutuantes onde a parte decimal precisa ser escrita após um ponto, que são as seguintes:
a)3.1416
k) 1,6
l) -106.688
Logo, analisando as alternativas só temos uma única variável que não se enquadra na sintaxe apresentada que é a alternativa K, porque utiliza uma vírgula para separar a parte inteira da parte decimal e o Matlab não entende isso como o número 1,6 mas sim como duas variáveis diferentes o número 1 se torna uma variável e o número 6 vai se tornar uma outra variável qualquer.
Resposta
As alternativas que não são aceitáveis no matlab são as alternativas j) , k) e b).
Exercício Resolvido #2
“Elaboração Própria”
- Estabelecer quais das seguintes constantes são do tipo inteiro e quais são do tipo flutuante no Matlab?
a) 0b) 0.55c) 0.0d) -3.0
e) 1f) 300g) 10.0h) 22
Passo 1
Para responder esse enunciado precisamos apenas lembrar das definições de variável inteira e flutuante pois o enunciado pede para classificarmos as alternativas entre elas.
Uma variável inteira como o nome já fala é uma variável cuja representação pode ser dada sob a forma de um número inteiro.
Uma variável do tipo flutuante são as variáveis que são representadas sob a forma de um número decimal.
Passo 2
Agora que temos as definições em mente vamos classificar as variáveis, primeiramente vamos começar com as variáveis do tipo inteira, pois, nessas alternativas temos umas pegadinhas.
Só de olhar, a gente consegue identificar que as alternativas a), e), f) e h) são números inteiros.
Porém, devemos perceber que 10.0 ainda é o número 10. E -3.0 é o número inteiro -3. Ou seja, as variáveis c), d) e g) também são do tipo inteiro.
Passo 3
Agora que definimos as do tipo inteira vamos utilizar a definição das flutuantes para definir as variáveis flutuantes.
A única variável que só pode ser expressa por um número decimal é a alternativa b).
Resposta
A única variável flutuante é a alternativa b) as demais são do tipo inteiro.
Exercício Resolvido #3
Fonte do Exercício. “Elaboração Própria”
Escrever cada um dos seguintes números como constantes Matlab. Em seguida, estabeleça o seu tipo:
a) 5,0b) 0,185c) meio d) zero
e) 3/2f) 0,0031416x103g) πh) 0,1x10-4
Passo 1
A questão em si pede para escrever cada variável dessa no Matlab, e em seguida classificá-las em qual tipo elas estão incluídas.
Passo 2
Primeiramente vamos incluir cada variável dessa no Matlab, belezinha?
Logo cada variável dessa no Matlab é escrita da seguinte forma:
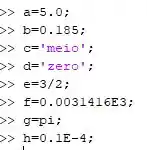
Passo 3
Agora que inserimos as variáveis no Matlab vamos classificá-las uma a uma.
- Aqui nós podemos ver que temos um número que pode ser escrito sob a forma de um número inteiro, então essa variável no Matlab é classificada como inteira.
- Já aqui essa variável não pode ser escrita sob a forma de um número inteiro, logo ela é classificada no Matlab como uma variável flutuante.
- Aqui nós temos um texto, então essas variáveis do tipo texto são chamadas de strings
- Aqui nós temos outro texto, então essas variáveis do tipo texto são chamadas de strings
- Temos aqui uma fração que é uma variável que não pode ser escrita de forma inteira então ela só pode ser flutuante.
- Aqui temos um número escrito na base 10, quando vamos desfazer essa notação temos um valor numérico de 3,14 que não pode ser escrito de forma inteira o classificando como um flutuante.
- Pi também é um número que não pode ser escrito sob a forma de um número inteiro o classificando como um flutuante.
- Aqui é um número menor do que 1 e também não pode ser escrito sob a forma de um número inteiro o classificando como flutuante.
Resposta
Ei, a resposta está no passo a passo :)
Exercício Resolvido #4
Fonte do Exercício. Ex.: “UFRJ – Cálculo 1 – P2 – 2020.2” ou “Elaboração Própria”
Quais dos seguintes são nomes de variáveis válidos em Matlab?
a) IRENEb) JOSE LUIZ c) VOLTS
d) JOLTSe) X+Yf) 3P
g) CAÇAh) CASSAi) VETOR
Passo 1
Para a resolução dessa questão precisamos lembrar de duas regrinhas básicas para a nomeação de uma variável que é começar sempre por letra e não pode ter caractere especial.
Analisando as alternativas todas acima seguem esse padrão com exceção das
b) começa com letra porém tem um espaçamento “Jose Luiz” .
e) começa com letra mas possui o símbolo “+”
f) não começa com letra.
g) também começa com letra maiúscula mas possui o “ç”.
Excluindo essas alternativas as demais são nomes de variáveis validas para o Matlab.
Resposta
Ei, a resposta está no passo a passo :)
Exercício Resolvido #5
Fonte do Exercício. “Elaboração Própria”
Escreva as seguintes expressões algébricas como expressões simbólicas no Matlab.
a) b) c)
Passo 1
O foco do exercício, assim como a teoria, é ensinar ao aluno a implementar tanto variáveis quanto funções simbólicas.
Para resolver essa questão, você precisa se lembrar que se declara uma variável simbólica através do comando syms.
Primeiramente indicamos o que é simbólico e depois escrevemos a função, do mesmo jeito que ela aparece no enunciado mesmo. Então a linha de raciocínio para responder cada alternativa é a seguinte:
1- determinação das variáveis simbólicas
2-implementação da função
Passo 2
a) ![]()
Sendo assim, para implementar a primeira alternativa precisamos deduzir quais variáveis são simbólicas. Como temos uma função F que depende apenas de y, temos que a única variável simbólica é o y.
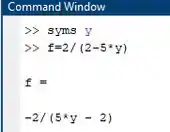
Então declaramos o y como simbólico e depois escrevemos a função.
Syms y
F=2/(2-5y)

Passo 3
b) 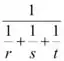
Seguindo a mesma lógica para a resolução da segunda alternativa, temos que as variáveis simbólicas são as variáveis r,s e t, pois a função depende desses três parâmetros.
Syms r s t
F=1/(1/r+1/s+1/t)
Passo 4
c) ![]()
E analogamente, temos que a última alternativa se torna:
syms b h
F=1/3*b*h

Resposta
Exercício Resolvido #6
Fonte do Exercício. “Elaboração Própria”
Descreva a importância das variáveis durante o desenvolvimento e execução de um programa em Matlab.
Passo 1
As variáveis possuem extrema importância no desenvolvimento de um código em Matlab, pois são as variáveis que armazenam as informações que o código irá processar. Por exemplo, para fazer um cálculo, é preciso armazenar os valores em variáveis.
Então se não existir uma variável para armazenar não tem informação para o código processar logo o código não funciona, sendo assim, não gera resultados.
Resposta
Ei, a resposta está no passo a passo :)
Exercício Resolvido #7
Fonte do Exercício. “Elaboração Própria”
Dadas as funções:
Encontre uma função que dependa apenas das variáveis .
Passo 1
O exercício aqui entrega duas funções e pede para você encontrar a função composta.
A ideia de funções compostas é altamente importante independente da área, por exemplo na programação gostamos de dividir essas funções dessa forma pois gera um código mais organizado, imagine só você colocar a função dentro da função e sair resolvendo as operações, bem complicado né?

Então, estamos aqui para te ensinar uma forma mais prática, preparado? vamos láá
A ideia aqui é pegar a função e substituí-lo dentro da função .
Para te mostrar que se você gera uma função e na linha seguinte essa função vira uma variável da , o Matlab entende que o resultado da precisa ser jogado como entrada na função .
Então vamos fazer utilizando as variáveis simbólicas pois não temos os valores das variáveis e além disso, queremos encontrar uma expressão no final de tudo e não um valor numérico. Quando acontecer essas duas coisas, você já tem que se lembrar das variáveis simbólicas!
Sendo assim o passo a passo é o seguinte:
1-Introdução das variáveis simbólicas.
2- Implementação da função
3- Implementação da função
Passo 2
Agora que criamos o passo a passo vamos apenas implementar as variáveis no Matlab.
Primeiramente vamos implementar as variáveis simbólicas do código, para isso temos:
Uma vez que criamos as variáveis simbólicas vamos criar a função
Agora vamos implementar a função
Passo 3
Se digitou tudo certinho no seu Matlab deve aparecer algo mais ou menos assim:
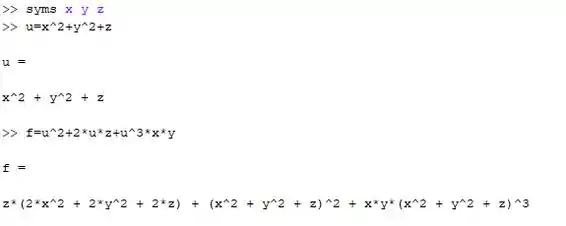
Resposta

Exercício Resolvido #8
Fonte do Exercício. “Elaboração Própria”
Na teoria do cálculo diferencial e integral aprendemos que certas integrais são bem complicadas de resolver, uma delas é a seguinte integral:
Através de técnicas desenvolvidas na disciplina nos é mostrado que essa integral gera a seguinte primitiva:
Utilize a função para comprovar que o Matlab realmente consegue calcular essas integrais.
Dica: a sintaxe da função int é a seguinte , e para o command window a função é escrita como l
Passo 1
Essa questão é uma aplicação de variável simbólica, uma ideia intuitiva para deduzir isso é que não temos valores nenhum das variáveis
Mas o correto pare se pensar é que estamos atrás de uma expressão final, uma função propriamente dita e o Matlab só consegue imprimir funções quando trabalhamos com variáveis simbólicas.
A ideia aqui é pegar a função e integrar utilizando a função int. A função int é uma função do Matlab que é utilizada para o cálculo de integrais simbólicas.
Sendo assim, o passo a passo para resolução do exercício é o seguinte:
1-Introdução das variáveis simbólicas, que no caso é a variável X.
2- Implementação da função
3- Implementação da função
4-Comparar com o resultado fornecido e verificar se realmente apresentam os mesmos resultados.
Passo 2
Agora que criamos o passo a passo, vamos apenas implementar as variáveis no Matlab.
Primeiramente vamos começar pela parte mais importante que é implementar as variáveis simbólicas do código. Como podemos ver, o logaritmo depende apenas de um único parâmetro que é o X. Sendo assim, a variável independente vai ser nossa variável simbólica.
Então, a variável simbólica é:
Uma vez que criamos as variáveis simbólicas vamos criar a função
Agora vamos implementar a função
Passo 3
Se digitou tudo certinho no seu Matlab deve aparecer algo mais ou menos assim:

Executando o programa deverá aparecer na sua janela de command window a seguinte informação:

Olhando a uma primeira visão não parece a mesma coisa né?
Mas, realizando as distributivas temos que:
Tem uma diferença da integral analítica que é dada pela soma de uma constante que é a constante de integração.
Resposta