Funções Predefinidas
Produzido por Gustavo BarbosaTeoria
E depois da tempestade....
Iaê galerinha.... Aula passada foi difícil né?

Sei como é, quando vi aquilo pela primeira vez também achei, mas vamos para outro papinho?
Juro que essa conversa aqui vai ser mais light e beeeeeeeeeeeeem mais prática.
Bem pessoal, hoje finalizaremos a nossa introdução ao Matlab e aqui iremos estudar algumas funções predefinidas que servem para nos auxiliar em diversas áreas e aposto que algumas delas você irá amar, eeeeeeeeee vamos lá.
Bem, já foi falado na primeira aula que o Matlab funciona como uma espécie de calculadora, então se você olhar na sua calculadora existe um bocado de função com algumas matemáticas e se a sua for mais sofisticada pode ter até diferenciação e integração, mas... o “Matlab tem isso? ”
Para a NOOOOOOOOOOOOSA ALEGRIA tem sim, e são sobre essas funções que iremos conversar hoje.
Funções Matemáticas
Assim como toda calculadora, o Matlab também possui funções matemáticas e elas são diversas, aqui iremos listar algumas das mais utilizadas na engenharia para que possamos nos situar.

Por exemplo, vamos supor que você quer retirar a raiz quadrada de 4, basta escrever o seguinte código:
E sabe o que vai sair? Isso ae .

Outro exemplo é se quisermos calcular a raiz de -4.
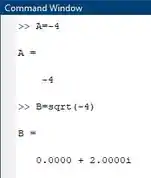
OPAA, olha só, o Matlab também processa números complexos, e a forma de escrevê-los é do jeito que está ai, primeiramente a parte real é uma constante seguindo as mesmas lógicas e depois a parte imaginária se multiplica por i.
Função de integração.
No Matlab existem dois tipos de integração a numérica e a simbólica, a integração numérica é uma espécie de algorítmo que serve para realizar a integração de pontos experimentais e obter uma expressão aproximada, isso será visto em cursos futuros.
Aqui no momento o nosso foco é a integração simbólica, que é aquela integração que você aprendeu no cálculo diferencial e essas funções de integração simbólica só operam em funções simbólicas, para nossa sorte só existe um único comando que é o comando .
Para entendermos a sintaxe vamos fazer uns exemplos...
Primeiramente devemos definir as variáveis simbólicas:
Depois vamos inserir a função simbólica:
E agora iremos integrar.
Então...

Então, de uma forma geral, a sintaxe da função é :
Se a integral for definida ainda podemos generalizar mais
Funções de derivação.
Assim como na integração, existe a diferenciação numérica e simbólica, mas o foco aqui será a diferenciação simbólica belezinha?
Então vamos lá:
Na derivação as mais importantes para a engenharia é a função e a função e igualmente a integração ambas operam sobre variáveis simbólicas.
Galera, a função diff ela tira a derivada da função, para deixar mais claro vamos fazer um exemplo:
Da mesma forma iremos escrever primeiramente as variáveis simbólicas e as funções:
Para derivar precisamos fazer e se você fez tudo certinho deve aparecer algo assim:

E assim podemos obter qualquer derivada cavernosa, e isso funciona também como derivada parcial, olha só:

Isso é possível porque ele considera tudo símbolo excerto a variável que está na função diferenciação ou integração.
Outra função muito utilizada é a famosa função gradiente, que é aquele mesmo vetorzinho que você vê em cálculo diferencial, aqui existe uma função destinada a seu cálculo que é a função .
Vamos resolver a seguinte função
E simplesmente vamos utilizar .

Fora essas duas existem mais três que são utilizadas em cursos avançados de cálculo, mas é pouco vista em programação destinada a engenharia, elas são a divergência e o laplaciano, o laplaciano iremos ver aqui, porém, para o cálculo do divergente precisamos entrar com um vetor simbólico e a criação de vetores será um tópico das próximas aulas.
Então, faremos um exemplo com laplaciano, ok?

Logo, para a derivada, a sintaxe geral é:
Se quer tirar o gradiente, divergente ou laplaciano já que deriva todas as variáveis só precisa do
Opa galera, existem outras funcionalidades no Matlab, mas acredito que essas aqui são as mais importantes, como já foi falado essa parte é bem prática e precisa realmente treinar, devido a isso selecionamos alguns exercícios com todo carinho do mundo para vocês treinar, então nos vemos lá.
Função de integração.
Funções de derivação.
Exercícios Resolvidos
Exercício Resolvido #1
Elaboração Própria
Calcule as funções abaixo utilizando o Matlab;
- Exponencial de 5
- Raiz quadrada de 4
- Raiz cúbica de 8
- Cosseno de (obs: no matlab é escrito como pi)
Passo 1
E aí galerinha? Vamos resolver mais uma questão de programação?
Essa questão é bem prática e, basicamente, é brincar com a tabela de funções. Essa tabelinha bonita aqui!

Passo 2
Pra vocês verem exatamente como fica no Matlab, já vou colocar os cálculos na janela do command window.
- A exponencial de x fica exp(x). Então a exponencial de 5 fica exp(5)
- Pra achar a raiz quadrada de x, fazemos sqrt(x). Então a raiz quadrada de 4 é sqrt(4).
- Não tem função pra raíz cúbica. Então vamos elevar ao expoente ⅓.
- O cosseno é bem simples ne, é bem como a gente escreve na matemática mesmo. E o nosso π vai ser do jeito que a gente fala (pi).

Passo 3

Passo 4
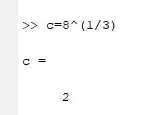
Passo 5

Resposta
- 148,4132
- 2
- 2
- 0,7071
Exercício Resolvido #2
Elaboração Própria
Em termodinâmica podemos calcular o trabalho da expansão de um gás utilizando a expressão:
Utilize a equação de Estado de Wan der Walls para calcular o trabalho de expansão de um gás de Wan der Walls
Obs: Equação de wan der walls
Passo 1
E aí, pessoal? Tudo bom?
Nessa questão, vamos precisar fazer uma integração simbólica. O primeiro passo é a inserção da função como uma função simbólica. Para isso primeiro precisa introduzir as variáveis simbólicas.
Olhando o problema temos que as variáveis são a, b, V, R e T, sendo assim:
E a função é dada por:
Se tudo foi feito direitinho devemos ter algo do tipo:

Passo 2
O passo 2 é integrar a função e, uma vez que a integral é indefinida, apenas precisamos utilizar a forma padrão da função e a variavel de integração é o V.
No Matlab fica assim:
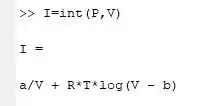
SIIIIIIIIM uma coisa importante o Matlab não conta a constante de integração +C então se estiver fazendo uma prova de cálculo ou algo que precise dele não esquece de somar ela tá?
Daí fica assim:
Resposta
Exercício Resolvido #3
Elaboração Própria
Em eletrodinâmica podemos calcular a força entre duas partículas a partir do potencial elétrico utilizando a seguinte expressão:
Utilize a expressão do potencial elétrico para calcular a força entre duas partículas carregadas
Obs: Equação Força é dada por
Passo 1
Fala aí galerinha! O primeiro passo, para fazer uma diferenciação simbólica, é a inserção da função como uma função simbólica. E, para isso, primeiro precisamos introduzir as variáveis simbólicas.
Mas como sabemos que a questão é de variável simbólica? Ou até mesmo quais variáveis são simbólicas?
Bem pessoal, existem diversas formas de deduzir isso, mas a forma mais comum é você perceber que o que a questão está te pedindo é uma expressão.
Em geral, o Matlab gera como saída algum número, então quando a questão te pede uma letra ou uma expressão pode confiar que o problema tem alguma base nas variáveis simbólicas, belezinha?
E para completar precisamos definir quais variáveis são simbólicas né?
As variáveis simbólicas são todas aquelas variáveis pela qual a sua função simbólica depende, ou seja, nessa questão corresponde às variáveis .
Passo 2
Utilizando as informações do passo 1 precisamos implementar as variáveis simbólicas no Matlab, que corresponde a:
Onde a função syms é a função que utilizamos para indicar que as variáveis que vem depois dela é tudo variável simbólica, ok?
consequentemente a função simbólica é dada por:
Se tudo foi feito direitinho devemos ter algo do tipo:
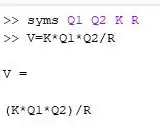
Passo 3
O próximo passo é derivar a função e, para isso, apenas precisamos utilizar a forma padrão da função que vimos na aula. A variável de derivação é o R.
Se você digitou tudo certinho no seu Matlab deve mostrar algo mais ou menos assim:

Resposta
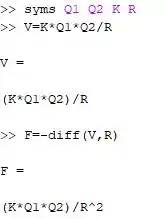
Exercício Resolvido #4
Elaboração Própria
Em eletrodinâmica podemos calcular a força entre duas partículas a partir do potencial elétrico utilizando as seguintes expressões:
Utilize a expressão do potencial elétrico para calcular a força entre duas partículas carregadas
Obs: Equação do potencial é dado por e lembrar que
Passo 1
Fala aí, pessoal! O primeiro passo pra fazer uma diferenciação simbólica é a inserção da função como uma função simbólica e, para isso, primeiro precisa introduzir as variáveis simbólicas.
Olhando o problema, temos que as variáveis são Q1, Q2, K e o R, sendo assim:
E a função é dada por:
Se tudo foi feito direitinho devemos ter algo do tipo:

Passo 2
O passo 2 é obter o gradiente da função, que pode ser obtido apenas utilizando a função gradient, logo:

Socorro, que resposta enorme é essa? Parece que temos 5 derivadas, sendo que nós temos apenas duas componentes de força....

Relaxaaaaaa você não fez nada de errado. É que a função gradient deriva a função em relação a todas as variaveis adicionadas. Então toma cuidado com isso ok?
Mas lembra as demais expressões:
Então so iremos pegar as derivadas em relação a x e a y que corresponde as duas ultimas linhas do nosso resultado.

Resposta
Ei, a resposta está no passo a passo :)
Exercício Resolvido #5
Elaboração Própria
Quando estudamos Mecânica dos materiais vimos de forma aprofundada como calcular a distribuição de força por unidade de área em sistemas deformáveis, uma dessas forças é chamada de tensão de cisalhamento e pode ser calculada para um solido linear pela expressão:
Utilize a seguinte expressão para o cálculo dessa força de cisalhamento:
Passo 1
O primeiro passo como foi visto na teoria é a inserção da função como uma função simbólica. Para isso, primeiro precisamos introduzir as variáveis simbólicas.
Olhando o problema temos que as variáveis são x e y sendo assim:
E a função é dada por:
Se tudo foi feito direitinho devemos ter algo do tipo:

Passo 2
O segundo passo é tirar o laplaciano da expressão anterior
Se tudo foi feito certinho, vai aparecer algo assim na sua tela:

Passo 3
Agora que temos as expressões basta integrar em relação a uma variável e depois a outra, logo:
E finalmente ira aparecer a resposta final na sua tela:
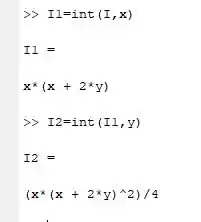
E essa é a função que vai descrever a distribuição de força ao longo de um solido linear deformável.
Resposta
Exercício Resolvido #6
Elaboração Própria
A distância de um ponto a reta é dada por:
Determine a distância do ponto a reta Primeiramente, declare as variáveis então calcule
Passo 1
E aí galerinha? Vamos resolver mais uma questão de programação?
Essa é uma questão de cálculo simples, onde primeiramente precisamos implementar a entrada de dados, que são as coordenadas do ponto e os coeficientes da reta. E então, a partir da fórmula dada pelo enunciado, iremos calcular a distância da reta até o ponto, usando funções matemáticas predefinidas existentes no Matlab.
É um tipo de questão bastante útil para o cálculo vetorial, então essa é uma ferramenta bastante útil para te ajudar a resolvê-las, ok?
Então precisamos seguir os seguintes passos para criar o programinha:
1.Entrada de dados – Inserir as variáveis
2.Cálculo do numerador
3.Cálculo do denominador
4.Cálculo da distância
Passo 2
Agora que sabemos o passo a passo precisamos transformá-los em uma linguagem de programação, beleza?
Vamos inserir o primeiro passo que é a entrada de dados, que basicamente definir os valores das 5 variáveis, sendo assim:
Agora que entramos com a entrada de dados precisamos criar o numerador e denominador.
Passo 3
Vamos começar com o numerador, que é um módulo, então para isso precisamos calcular o valor absoluto da expressão e essa função no matlab é a função , logo:
Agora vamos implementar o denominador, onde vemos a raiz dos coeficientes da equação da reta, logo para o cálculo do denominador precisamos utilizar a função para calcular a raiz quadrada, logo:
Por fim, a distância entre o ponto e a reta é
Passo 4
Se você digitou tudo certinho no Matlab vai aparecer as seguintes informações:

Resposta
Se tudo foi inscrito certinho o resultado é
Exercício Resolvido #7
Elaboração Própria
Declare duas variáveis: e e com isso calcule ambos os lados da seguinte igualdade:
Após calcular cada lado da equação confirme a existência da igualdade desta identidade trigonométrica.
Passo 1
E aí galerinha? Vamos resolver mais uma questão de programação?
Essa é uma questão de cálculo simples, onde primeiramente precisamos implementar a entrada de dados e a partir de funções predefinidas existentes no Matlab iremos calcular essa igualdade trigonométrica.
Então para isso precisamos seguir os seguintes passos para criar o programinha:
1.Entrada de dados – Inserir as variáveis
2.Cálculo do termo a esquerda da igualdade
3.Cálculo do termo a direita da igualdade
Passo 2
Agora que sabemos o passo a passo precisamos transformá-los em uma linguagem de programação, belezinha?
Vamos inserir o primeiro passo que é a entrada de dados, que basicamente é programar os dados disponibilizados, sendo assim:
Agora que entramos com a entrada de dados precisamos calcular o lado esquerdo e direito da identidade acima, então para isso precisamos calcular cada etapa.
Sendo assim, primeiramente vamos começar com o lado esquerdo e para isso precisamos calcular o valor das diferenças do cosseno, sendo assim:
Agora vamos implementar o lado direito da equação, onde vamos calcular os produtos de seno. Lembrando que o seno no Matlab é chamado de , sendo assim:
Passo 3
Se você digitou tudo certinho no Matlab vai aparecer as seguintes informações:

Resposta
Logo analisando o Resultado vemos que essa igualdade não existe para esse valor de e , logo essa igualdade não é válida.
Exercício Resolvido #8
Elaboração Própria
Em cálculo de reatores batelada uma das grandezas mais importantes para o dimensionamento é o tempo de reação.
Um reator Batelada é modelo de reator cuja a reação varia no tempo, em geral, é bastante utilizado em sistemas de produção de medicamentos e processos de produção de etanol, a equação que dita qual é o tempo do processo é dada por:
Onde é a concentração do reagente limitante e é uma função que dita como a concentração do componente varia dentro do reator.
Através de medidas experimentais um grupo de alunos encontrou a seguinte expressão para o
Onde é uma constante de proporcionalidade e a concentração do componente é dada por:
Utilizando essas informações encontre uma expressão para o cálculo do tempo do processo.
Passo 1
E aí galerinha? Vamos resolver mais uma questão de programação?
Essa é uma questão que é bastante vista em cursos de reatores químicos, em geral o tempo do processo é a chave para dimensionar e projetar o reator, belezinha?
Aqui você vai ver como a gente calcula esse tempo a partir de uma equação estimada através de dados experimentais, sendo assim precisamos de duas coisas aqui.
Primeiramente é as variáveis simbólicas e segundamente é a função .
Então para isso precisamos seguir os seguintes passos para criar o programinha:
1.Entrada de dados – Inserir as variáveis simbólicas e as funções disponibilizadas no problema.
2.Cálculo da integral através da função do Matlab.
Passo 2
Agora que sabemos o passo a passo precisamos transforma-los em uma linguagem de programação, belezinha?
Vamos inserir o primeiro passo que é a entrada de dados, que basicamente é programar os dados disponibilizados, sendo assim:
Agora que entramos com a entrada de dados precisamos calcular a integral para assim encontrar uma expressão para o tempo, portanto:
Passo 3
Se você digitou tudo certinho no Matlab vai aparecer as seguintes informações:

Resposta
Logo, a sua resposta deve ser algo parecido com isso aqui:
![]()