Recursos Gráficos do Simulink
Produzido por Gustavo BarbosaTeoria
Introdução
Olá, jovens! Espero que estejam animados para a aula de hoje, pois eu estou! Hoje vamos aprender a mudar alguns parâmetros de simulação no SIMULINK e a mexer em algumas coisas nos gráficos, como zoom, escala dos eixos, etc. Além disso, vamos conhecer um bloco que permite plotar várias curvas no mesmo gráfico gerado pelo “Scope”.
Se ajeitem nas cadeiras, que vamos começar!

Alterando os parâmetros de simulação
Digamos que você queira gerar o gráfico de uma onda senoidal no SIMULINK com uma duração de . Crie um novo modelo, adicione os blocos “Sine Wave” e “Scope” e os interligue:

E como faz para indicar que queremos que a onda dure ? Na barra superior da janela onde construímos os modelos, existe um campo onde podemos alterar o tempo de duração da simulação, como o destacado abaixo. Esse tempo é dado em segundos e a simulação dura por padrão.

Outra alternativa é mudar o instante final da simulação nos parâmetros de simulação, acessando-os no “Model Configuration Parameters”. Para abrir o “Model Configuration Parameters”, clique sobre a engrenagem da barra superior (destacada em vermelho abaixo) ou clicando em:
Simulation -> Model Configuration Parameters (destacado em azul abaixo)

Ao executar uma dessas duas ações, aparecerá a janela abaixo, chamada de “Configuration Parameters”. À esquerda, temos um menu com vários conjuntos de parâmetros de simulação. Normalmente, alteramos os parâmetros que estão na opção “Solver” (destacado abaixo), a primeira opção do menu e a que aparece automaticamente quando abrimos o “Configuration Parameter” (como é o caso da imagem abaixo).
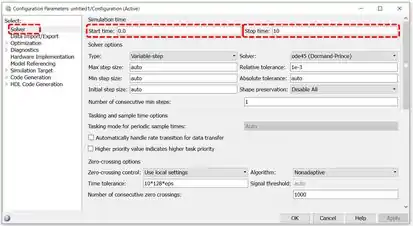
Em “Solver”, podemos alterar o tempo de simulação, mudado o instante de início e o instante final nos campos destacados na imagem. Os instantes são dados em segundos. Note que que o instante final por padrão é , como descrito acima.
Existem outros parâmetros de simulação que podemos alterar em “Solver”, como o algoritmo para resolver equações diferenciais e o tamanho do passo. Na aula de hoje, veremos somente como alterar o tempo de simulação e o tamanho do passo, que vocês verão mais pra frente por quê.
Após alterar algum parâmetro em “Configuration Parameters”, clique em “OK” para fechar as alterações serem implementadas e a janela se fechar automaticamente.
Para a nossa onda senoidal, vamos alterar o instante final para . Você pode fazer usando qualquer uma das duas alternativas que apresentei:
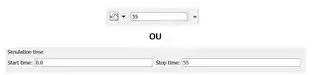
Vamos rodar a simulação e ver como ficou o gráfico da nossa onda senoidal. Clique em “Run” e, quando o SIMULINK tiver terminado de rodar o modelo, clique duas vezes no bloco “Scope”, para abrir o gráfico. Ele sairá com essa cara:
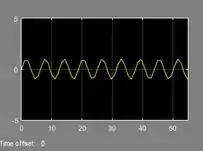
Essa onda tá meio tortinha, meio “quebradona” demais, né? Para ela ficar mais redondinha, precisamos mudar dois parâmetros de simulação, lá no “Solver” do “Configuration Parameters”: o tamanho mínimo e máximo do passo do algoritmo da simulação.
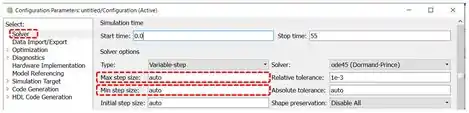
Por padrão, eles são calculados automaticamente. Devemos colocar no lugar valores bem pequenas, da ordem de . Para chegar num tamanho bom, é meio por “tentativa e erro” e depende do que você estiver modelando. Eu adotei os valores abaixo, mas você pode tentar outros valores, se quiser, pra ver o que acontece.
![]()
Clique em “OK” e rode a simulação de novo. Se você clicar duas vezes no “Scope”, você terá o novo gráfico:
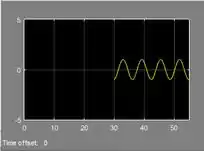
Vixe, perdemos um pedaço do gráfico! Esse efeito se chama “amnésia” e vamos ver como contornamos isso.
Para corrigir a amnésia, devemos mudar uma propriedade do bloco “Scope”. Para acessar as propriedades de “Scope”, na janela do gráfico, clique na engrenagem destacada abaixo. Uma janela chamada “Scope parameters” se abrirá. Vá na aba “History”, onde tem a propriedade “Limit data points to last”, também destacado na imagem abaixo:
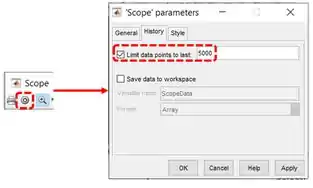
O valor padrão desse campo é de . Para corrigirmos a amnésia, devemos aumentar esse número. Novamente, é meio por “tentativa e erro”. Eu recomendo ir multiplicando por até obter um resultado satisfatório. Logo, vamos mudar esse valor para .
Após alterar o valor, clique em “OK”, feche o gráfico e rode a simulação novamente. O novo grafico terá essa cara:

Agora ele está completinho, indo de a =)
Alterando eixos e zoom dos gráficos
Tem um espação sobrando no nosso gráfico da onda senoidal, não acha? Para a onda preencher o espaço disponível, podemos mudar a escala do gráfico. Na barra de ferramentas na parte superior da janela com o gráfico, temos um botão chamado “Autoscale” (destacado abaixo), que ajusta a escala do gráfico de forma que ele ocupe a janela inteira.

Quando clicamos nesse botão no gráfico da onda senoidal, a escala do eixo vertical do gráfico se adapta à amplitude da onda:

O SIMULINK oferece outras opções de zoom para os gráficos do “Scope”. Temos o botão “Zoom” (destacado em vermelho abaixo), que amplia a região do gráfico na região onde clicamos. Também podemos mudar a escala do eixo horizontal manualmente, usando o botão “Zoom X-axis” (destacado em azul abaixo), ou muda a escala do eixo vertical, por meio do botão “Zoom Y-axis” (destacado em amarelo abaixo).
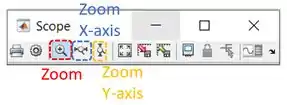
Outra coisa que podemos fazer é aumentar o número de subgráficos em uma mesma janela do “Scope”. Para isto, na janela do gráfico, clique na engrenagem que nos permite ver as propriedades do “Scope”, para abrir a janela “Scope parameters”. Na aba “General”, existe uma propriedade chamada “Number of axes” (destacada na imagem abaixo). Por padrão, ela é igual a e significa que teremos somente um gráfico na janela do “Scope”.
Altere esse valor para e clique em “OK”. Você verá que a janela do “Scope” agora possui dois subgráficos vazios, como na iamgem abaixo.
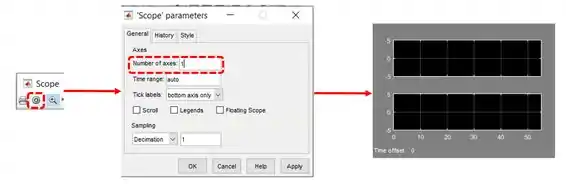
Feche a janela do “Scope” e repare que o bloco “Scope” ganhou uma setinha de entrada a mais:
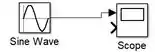
Isso significa que devemos adicionar mais um sinal para o “Scope” gerar o segundo gráfico e preencher aqueles subgráficos vazios. Vamos adicionar no modelo o bloco da rampa e ligá-lo ao “Scope”:
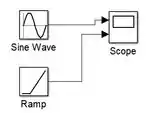
Vamos rodar a simulação novamente e ver como ficaram os gráficos:

Agora temos dois gráficos na mesma janela =D
Bloco mux
“Mas e se eu quiser ter duas curvas no mesmo gráfico, em vez de uma em cada gráfico?”
Para isto, você pode usar o bloco “Mux”, da biblioteca “Signal Routing”, apresentada abaixo com o “Mux” destacado:

O bloco “Mux” combina dois sinais de entrada (ou mais!) em uma única saída. Você pode indicar o número entradas alterando as propriedades do bloco.
Vamos ver como ele funciona plotando a onda senoidal e a rampa da seção anterior no mesmo gráfico. Para isto, altere o modelo que fizemos, deletando as conexões entre os blocos, alterando o número de entradas do “Scope” e incluindo o bloco “Mux” no modelo.
Em seguida, conecte os blocos da onda senoidal e da rampa nas duas entradas do “Mux”; e conecte a saída do “Mux” com a entrada do “Scope”. O modelo vai ficar com essa cara:

Rode a simulação e clique duas vezes sobre o “Scope”, para vermos o gráfico:
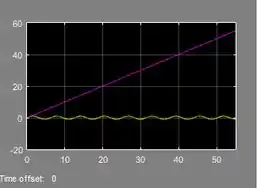
Tcharam! Temos um gráfico com duas curvas, a amarela representando a onda senoidal e a rosa, a rampa. Como as duas curvas estão na mesma escala e a rampa cresce continuamente durante os da simulação, a onda senoidal ficou achatadinha porque tem amplitude constante.
Caramba, vimos bastante coisa hoje, né? Bora praticar ;D
Alterando eixos e zoom dos gráficos
Bloco mux
Exercícios Resolvidos
Exercício Resolvido #1
“Elaboração Própria”
No SIMULINK, gere uma onda senoidal de frequência variável (bloco “Chirp Signal”) e a simule por . Gere um gráfico do sinal e ajuste sua escala.
Passo 1
Este exercício tem por objetivo praticar a alterar o tempo de simulação e ajustar a escala de um gráfico. O padrão no SIMULINK é o modelo seja simulado por e o enunciado pede que a simulação seja de .
O modelo deste exercício terá somente dois blocos: a entrada do modelo será o bloco “Chirp Signal” e a saída do modelo, um bloco “Scope”. Após fazermos a simulação, vamos abrir o gráfico da onda e ajustar a escala com o botão “Autoscale”.
Passo 2
Em um novo modelo, insira a entrada do modelo: o bloco “Chirp Signal”, que se encontra na biblioteca “Sources”:
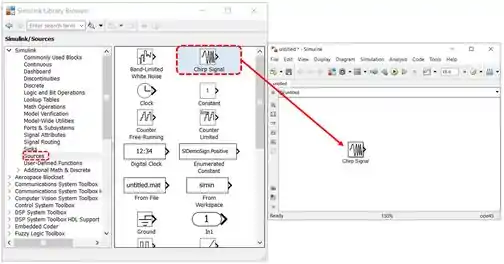
Como o enunciado não especificou propriedade alguma dessa onda senoidal com frequência variável, não mexeremos nos parâmetros de “Chirp Signal”.
Insira a saída do modelo, um bloco “Scope”, e conecte-o a “Chirp Signal”:
O modelo do exercício está pronto :)
Passo 3
O próximo passo é alterar o tempo de simulação para . Na barra superior da janela onde construímos os modelos, existe um campo onde podemos alterar o tempo de duração da simulação, destacado abaixo:
Repare que ali está escrito . Esse tempo é dado em segundos e é o padrão do SIMULINK. Troque esse valor por :
![]()
E rode a simulação. Ao término da execução, dê um duplo-clique sobre “Scope” para ver o gráfico da onda senoidal:
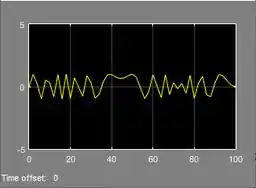
Repare que o eixo horizontal vai de a , bem como pedimos ao SIMULINK.
Passo 4
A curva está meio achatadinha, não acha? O enunciado pediu para ajustarmos a escala do gráfico. Para isto, usaremos o botão “Autoscale”, destacado abaixo:
![]()
Clique sobre ele e você verá que a curva vai ocupar o espaço vazio disponível.
Resposta
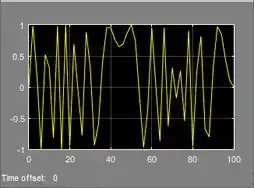
Exercício Resolvido #2
“Elaboração Própria”
No SIMULINK, gere uma onda senoidal de frequência variável (bloco “Chirp Signal”) e a simule por . Gere um gráfico do sinal e faça os ajustes necessários para melhorar a resolução do gráfico.
Passo 1
Este exercício tem por objetivo praticar a alterar alguns parâmetros de simulação, como o tempo de simulação (o padrão no SIMULINK é e o enunciado pede simulação de ) e o tamanho mínimo e máximo do passo do algoritmo da simulação (são eles que interferem na resolução do gráfico).
O modelo deste exercício terá somente dois blocos: a entrada do modelo será o bloco “Chirp Signal” e a saída do modelo, um bloco “Scope”. Após fazermos a simulação, vamos abrir o gráfico da onda e ver o que precisa ser ajustado.
Passo 2
Em um novo modelo, insira a entrada do modelo: o bloco “Chirp Signal”, que se encontra na biblioteca “Sources”. Não precisamos mexer em nenhum parâmetro de “Chirp Signal”, pois o enunciado não deu maiores detalhes sobre a onda senoidal com frequência variável.
Em seguida, insira a saída do modelo, um bloco “Scope”, e conecte-o a “Chirp Signal”:
O modelo do exercício está pronto, agora precisamos ajustar o tempo de simulação de para . Na barra superior da janela do modelo, no campo onde podemos alterar o tempo de duração da simulação, destacado abaixo, troque por .

Execute a simulação e veja como ficou o gráfico:

Passo 3
Vamos fazer com que a curva ocupe todo o espaço do gráfico apertando o botão “Autoscale”, destacado abaixo:
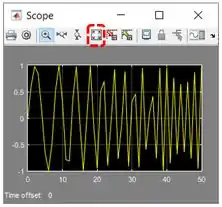
Ele está bem feio, né? A curva não está suave, não lembra nem um pouco uma onda senoidal. Para melhorar a aparência dela, vamos mudar dois parâmetros de simulação: o tamanho mínimo e máximo do passo do algoritmo da simulação.
Para acessar os parâmetros de simulação, clique sobre a engrenagem da barra superior da janela onde construímos os modelos (destacada em vermelho abaixo) ou clique em:
Simulation -> Model Configuration Parameters (destacado em azul abaixo)

Ao executar uma dessas duas ações, aparecerá a janela “Configuration Parameters”. No item “Solver”, estão os parâmetros que queremos ajustar para deixar a curva mais redonda (destacados em vermelho abaixo):
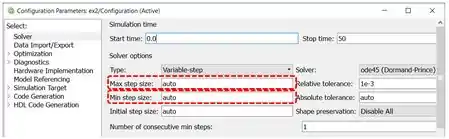
Por padrão, o tamanho mínimo e máximo do passo é calculado automaticamente. Para gerarmos curvas mais bonitinhas, devemos usar valores de passo bem pequenos, da ordem de . Eu adotei os valores abaixo, mas você pode usar os valores que quiser.
![]()
Clique em “OK”, feche a janela do “Scope” e rode a simulação de novo. Vamos ver como ficou o gráfico?

Tá faltando um pedaço dele =O
Passo 4
Para corrigir esse efeito de amnésia, vamos mudar uma propriedade do bloco “Scope” chamada “Limit data points to last”.
Para acessar as propriedades de “Scope”, na janela do gráfico com um pedaço faltando, clique na engrenagem destacada abaixo. Uma janela chamada “Scope parameters” se abrirá. Vá na aba “History”, onde tem a propriedade “Limit data points to last”, destacado abaixo:

O valor padrão desse campo é de e ele deve ser aumentado para corrigir o problema de faltar um pedaço da curva. Vamos mudar esse valor para , fechar a janela do “Scope” e rodar a simulação de novo.
Após concluir a simulação, clique duas vezes sobre o bloco “Scope” para ver o gráfico da onda senoidal, você vai ver que dessa vez ela estará completa =D
Resposta

Exercício Resolvido #3
“Elaboração Própria”
No SIMULINK, usando somente UM bloco “Scope”, gere os gráficos da onda e .
Ambos os gráficos devem estar na mesma janela, que deve conter dois subgráficos, um para cada onda.
Passo 1
Este exercício serve para praticar a alterar as propriedades do bloco “Scope”, de forma que ele tenha duas entradas e sua janela tenha dois subgráficos, um em cima do outro.
Um subgráfico terá a curva de e outro, a de . Para isto, construiremos um modelo com seis blocos:
- A entrada do modelo é composta por três blocos. Dois deles servirão para obter : um bloco “Constant”, que deverá ser igual a , e um bloco “Sine Wave”, representando o componente de . O terceiro bloco é um bloco “Constant”, que será igual a e servirá para gerar ;
- Um bloco “Add” para somar os dois blocos de entrada que produzem ;
- Um bloco “Product” para fazer o produto entre e o bloco “Constant” igual a , para gerar ;
- A saída do modelo será um bloco “Scope”, que plotará e .
Passo 2
Para construir o modelo, vamos começar pelas duas entradas para construir . Vá à biblioteca “Sources”, ache o bloco “Constant” e arraste-o para um modelo em branco. Em seguida, atribua a ele o valor de , alterando seus parâmetros dando um duplo-clique sobre o bloco:

No campo do parâmetro “Constant value”, destacado acima, altere o valor padrão de para .
Agora, adicione a segunda entrada para construir : o bloco “Sine Wave”. Ainda na biblioteca “Sources”, encontre o bloco “Sine Wave” e arraste-o para o modelo.
Como a onda que queremos criar é , sua amplitude é , sua frequência é e a sua fase é . Esses são os vlores padrão dos parâmetros desse bloco, como pode ser visto abaixo, destacado em vermelho:

Por isso, não precisamos alterar as propriedades de “Sine Wave”.
Após adicionar as duas entradas que geram , vamos inserir o bloco “Add” para somá-las. Na biblioteca “Math Operations”, procure o bloco “Add” e arraste-o para o nosso modelinho. Conecte os blocos “Constant” e “Sine Wave” a cada uma das entradas de “Add” e o modelo ficará com essa cara:

A saída de “Add” será , pois .
Passo 3
Vamos inserir a terceira e última entrada do modelo: um bloco “Constant” com valor de , que servirá para calcular . Vá à biblioteca “Sources” novamente para buscar o bloco. Arraste-o para o modelo e altere seu valor para . O modelo ficará assim:
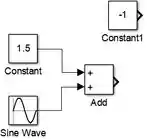
Vamos inserir o bloco “Product” que nos dará . O bloco “Product” multiplicará por , resultando em . Encontre-o na biblioteca “Math Operations”, arraste-o para o modelo e conecte o bloco “Constant” com valor e a saída de “Add” (que á função ) a cada uma das entradas de “Product”:

A saída de “Product” será .
Passo 4
Vamos inserir um bloco “Scope” para termos os gráficos de e conforme o enunciado pediu. Na biblioteca “Sink”, encontre o bloco “Scope” e insira-o no modelo:
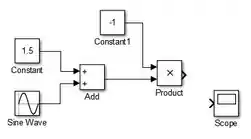
Para termos dois subgráficos em um bloco “Scope” devemos alterar seus parâmetros. Para isto, dê dois-cliques sobre o “Scope” para abrir sua janela. Em seguida clique na engrenagem que abre a janela com as propriedades do “Scope”, destacada abaixo.

A janela com as propriedades do “Scope” se chama “Scope parameters”. Na aba “General”, existe uma propriedade chamada “Number of axes” (destacada na imagem abaixo). Por padrão, ela é igual a e significa que teremos somente um gráfico na janela do “Scope”.
Altere esse valor para e clique em “OK”. Você verá que a janela do “Scope” agora possui dois subgráficos vazios, como na imagem abaixo.
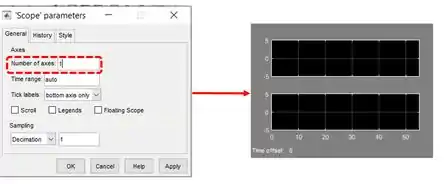
Feche a janela do “Scope” e repare que o bloco “Scope” ganhou uma setinha de entrada a mais:
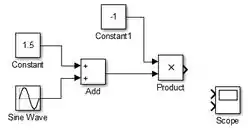
Conecte a saída de “Add” à entrada de cima do bloco “Scope”, para plotar no subgráfico de cima. Para isto, clique sobre a seta superior na lateral do “Scope” e arraste, aparecerá uma flecha vermelha tracejada. Conecte a outra ponta da flecha vermelha na linha conectando “Add” a “Product”:

Essa conexão faz com que a saída de “Add”, que é , vá para o bloco “Product” e para o bloco “Scope”. Dessa forma, consegue-se calcular e também plotar .
Conecte a saída de “Product” à entrada de baixo de “Scope”, para plotar no subgráfico de baixo:
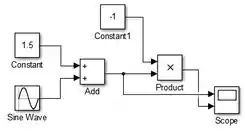
Modelo pronto! Para gerar os gráficos de e , rode o programa e, ao final da execução, dê um duplo-clique sobre o “Scope” para ver os gráficos.
Resposta
Exercício Resolvido #4
“Elaboração Própria”
No SIMULINK, usando um bloco “Scope” e um bloco “Mux”, gere um gráfico contendo as ondas e .
Passo 1
Este exercício serve para praticar o uso do bloco “Mux”, que combina múltiplos sinais de entrada em um único sinal de saída.
Construiremos um modelo com sete blocos:
- A entrada do modelo é composta por três blocos. Dois deles servirão para obter : um bloco “Constant”, que deverá ser igual a , e um bloco “Sine Wave”, para criar o componente de . O terceiro bloco é um bloco “Constant”, que será igual a e servirá para gerar ;
- Um bloco “Add” para somar os dois blocos de entrada que produzem ;
- Um bloco “Product” para fazer o produto entre e o bloco “Constant” igual a , para gerar ;
- Um bloco “Mux”, para combinar os sinais de e em um só;
- A saída do modelo será um bloco “Scope”, que plotará e em um mesmo gráfico.
Passo 2
Em um novo modelo, insira as duas entradas para construir . Vá à biblioteca “Sources” e arraste um bloco “Constant” para o modelo em branco. Em seguida, atribua a ele o valor de , alterando seus parâmetros.
Adicione a segunda entrada para construir : o bloco “Sine Wave”. Ainda na biblioteca “Sources”, encontre o bloco “Sine Wave” e arraste-o para o modelo.
Como a onda que queremos criar é , sua amplitude é , sua frequência é e a sua fase é . Esses são os valores padrão dos parâmetros desse bloco, por isso, não precisamos alterar as propriedades de “Sine Wave”.
Após adicionar as duas entradas que geram , vamos inserir o bloco “Add” para somá-las. Na biblioteca “Math Operations”, arraste o bloco “Add” para o modelo e conecte os blocos “Constant” e “Sine Wave” a cada uma das entradas de “Add”:
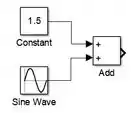
A saída de “Add” será , pois .
Passo 3
Agora vamos obter . Insira a terceira e última entrada do modelo: um bloco “Constant” com valor de :
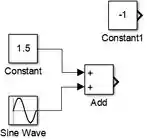
Em seguida, insira o bloco “Product”, que multiplicará por , resultando em . Encontre-o na biblioteca “Math Operations”, arraste-o para o modelo e conecte o bloco “Constant” com valor e a saída de “Add” (que á função ) a cada uma das entradas de “Product”:
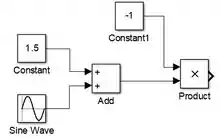
A saída de “Product” será .
Passo 4
Já temos os sinais de e . Hora de uni-los em um sinal só usando o bloco “Mux”! Vá à biblioteca “Signal Routing”, encontre o “Mux” e arraste-o para o modelo:

O padrão do bloco “Mux” é ter duas entradas e uma saída. Como queremos plotar só dois sinais no mesmo gráfico, não precisamos alterar as propriedades de “Mux”.
Conecte a saída de “Add” à entrada de cima do bloco “Mux”, para que seja a curva amarela do gráfico (como veremos no próximo passo). Para isto, clique sobre a seta superior na lateral do “Mux” e arraste, aparecerá uma flecha vermelha tracejada. Conecte a outra ponta da flecha vermelha na linha conectando “Add” a “Product”.
Em seguida, conecte a saída de “Product” à entrada de baixo de “Mux”, para que seja a curva rosa do gráfico:
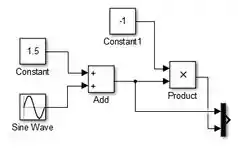
Na prática, você pode conectar na entrada de “Mux” que você quiser. Apenas fiz essas orientações para que no final saibamos qual curv é qual.
Passo 5
Vamos inserir a saída do modelo: um bloco “Scope”. Vá à biblioteca “Sinks”, arraste o bloco “Scope” para o modelo e conecte a saída de “Mux” à entrada de “Scope”:
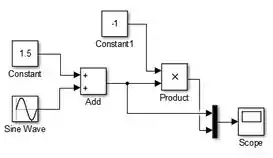
O modelo está pronto. Rode o programa e clique duas vezes sobre o “Scope” para visualizar o gráfico.
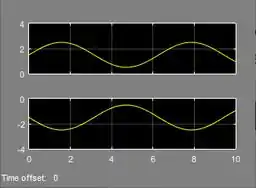
Resposta

é a curva amarela e é a curva rosa
Exercício Resolvido #5
“Elaboração Própria”
No SIMULINK, gere uma onda senoidal de frequência variável (bloco “Chirp Signal”) e a simule por .
- Gere um gráfico do sinal e faça os ajustes necessários para melhorar a resolução do gráfico;
- Utilizando o gráfico, faça uma estimativa da frequência inicial da onda.
Passo 1
Este exercício tem por objetivo praticar a mudança de parâmetros de simulação, como o tempo de simulação, e fazer ajustes no gráfico, de forma que ele fique mais agradável esteticamente. Além disso, vamos praticar a usar a ferramenta para mudar manualmente a escala do eixo horizontal do gráfico: o botão “Zoom X-axis”. Esse botão vai nos ajudar a determinar a frequência inicial da onda senoidal.
O modelo deste exercício terá somente dois blocos: a entrada do modelo será o bloco “Chirp Signal” e a saída do modelo, um bloco “Scope”. Após fazermos a simulação, vamos abrir o gráfico da onda, ver o que precisa ser ajustado e ajustar a escala do eixo horizontal para verificar a frequência inicial.
Passo 2
Vamos começar construindo o modelo de dois blocos. Em um novo modelo, insira um bloco “Chirp Signal”, da biblioteca “Sources”. Não mexa em nenhum parâmetro de “Chirp Signal”, pois o enunciado não especificou os parâmetros da onda senoidal com frequência variável.
Em seguida, insira um bloco “Scope”, e conecte-o a “Chirp Signal”. Dessa forma, o modelo está pronto e tem essa cara:

Antes de executar o programa, ajuste o tempo de simulação de para . Na barra superior da janela do modelo, no campo onde podemos alterar o tempo de duração da simulação, destacado abaixo, troque por .

Agora, vamos resolver a letra a do exercício. Rode a simulação e veja como ficou o gráfico. Utilize o botão “Autoscale”, destacado no print abaixo, para a curva se ajustar ao tamanho da janela:
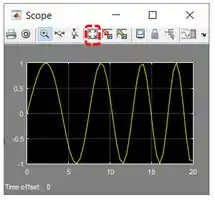
Passo 3
Perceba que a curva não está suave, os vales e as cristas estão “pontiagudos”. Para deixar a curva mais “redondinha”, temos que mudar o tamanho mínimo e máximo do passo do algoritmo da simulação.
Para acessar os parâmetros de simulação, clique sobre a engrenagem da barra superior da janela onde construímos os modelos (destacada em vermelho abaixo):

Aparecerá a janela “Configuration Parameters”. No item “Solver”, encontre os parâmetros “Max step size” (tamanho máximo de passo) e “Min step size” (tamanho mínimo de passo), destacados em vermelho abaixo:
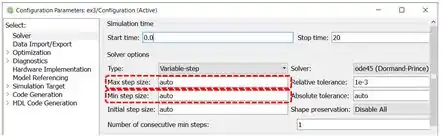
Eles são calculados automaticamente por padrão. Para termos curvs mais arredondadas, devemos usar valores de passo bem pequenos, da ordem de . Eu adotei os valores abaixo, mas você pode usar os valores que quiser.
![]()
Clique em “OK”, feche a janela do “Scope” e rode a simulação de novo:

A onda não está mais pontiaguda e não tivemos um problema de amnésia. Letra a resolvida =D
Passo 4
Vamos resolver a letra b, que pede para estimar a frequência inicial da onda a partir do gráfico. Para termos a resposta deste exercício, precisamos relembrar alguns elementos básicos de uma onda periódica:
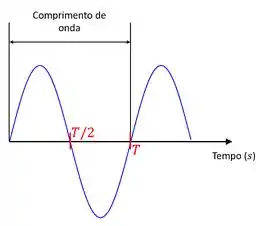
Um dos elementos de um onda periódica é o comprimento de onda, indicado na imagem acima. O comprimento de onda é a medida de um ciclo completo da onda, que pode ser medido entre uma crista e um vale, como indicado acima. Gosto de pensar que é medido considerando um “sobe e desce”
O período é o intervalo de tempo para se completar um ciclo de onda, isto é, o período é medido no intervalo de um comprimento de onda. Falando beeem simplificadamente, é o tempo de um “sobe e desce”. Ele é indicado na figura acima por um vermelho.
A frequência de uma onda é a quantidade de ciclos em um determinado intervalo de tempo. Em uma onda períodica, ela é o inverso do período:
Para estimarmos a frequência inicial da onda senoidal de frequência periódica pelo gráfico, devemos dar um zoom no primeiro “sobe e desce” da onda, no gráfico da janela do “Scope”. Para isto, usaremos o botão “Zoom X-axis”, destacado abaixo:
Clique no “Zoom X-axis” e, em seguida, clique no ponto próximo ao início da curva e arraste. Aparecerá uma linha horizontal, como a da figura abaixo. O comprimento dessa linha horizontal define o grau do zoom que você dará:
Arraste o ponto final da reta até abranger um “sobe e desce” da onda. O resultado final será mais ou menos assim:
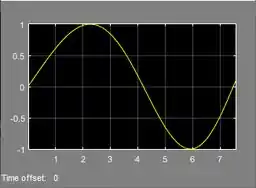
Passo 5
No gráfico acima, note que a crista é mais larga que o vale, indicando que elas têm frequência diferentes. Por isso, vamos usar só a crista para estimar a fequência inicial, considerando que o tempo de duração da crista vale :

Para determinar , vamos uma ferramenta que permite sabermos as coordenadas dos pontos do gráfico. Na barra de ferramentas da janela do “Scope”, onde você acabou de dar um zoom no gráfico, clique em “Try Time Scope”, indicado abaixo:

Perceba que apareceram ferramentas novas. Elas ajudam a analisar o gráfico. Para vermos as coordenadas da curva, clique no botão “Cursor Measurements” com o ícone de uma régua, destacado abaixo:
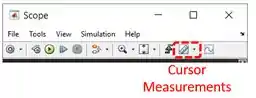
Aparecerão duas retas verticais no gráfico, com bolinhas onde elas interceptam a curva, e uma janela à direita, indicando as coordenadas dessas bolinhas:

Note que as retas são chamadas de e e na janela à direita, temos as coordenadas de tempo (eixo horizontal do gráfico) e amplitude (eixo vertical) para cada uma delas. Vamos olhar mais de perto a janelinha que dá as coordenadas:
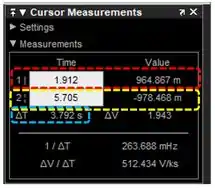
Destacado em vermelho, temos as coordenadas da reta e, em amarelo, da reta .
E, o mais importante para este exercício, em azul, temos a diferença entre as coordenadas de tempo das bolinhas da reta e da reta . Perceba no print acima que a coordenada da bolinha da reta no eixo horizontal é e que a da reta é . Em azul, temos o que é .
É nesse campo que obteremos para calcular a frequência inicial da onda.
Para isto, selecione a reta e arraste-a até o início do gráfico, isto é, até o começo da crista. Em seguida, selecione a reta e arraste-a até o final da crista. Dica: você pode usar as setinhas do teclado para levar as retas mais à direita ou à esquerda.
Sua janela ficará parecida com essa:
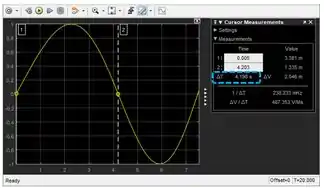
Veja o campo do , destacado em azul acima. O valor dele equivale a , logo, temos que:
Como a frequência é o inverso do período, temos:
Resposta
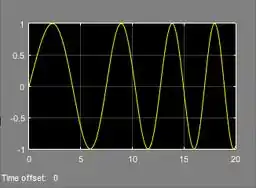
- Gráfico da onda senoidal de frequência variável:
- A frequência inicial da onda é de aproxidamente .
Exercício Resolvido #6
“Adaptado de UFMG – Learning.m: Uma apostila de introdução às ferramentas do MATLAB. PET Engenharia Elétrica (2020). Exercício 10.3”
Crie um novo modelo. Utilizando os blocos “Sine Wave”, “Mux” e “Scope”, mostre em um mesmo osciloscópio as funções:
Passo 1
O exercício pede para plotarmos três curvas, cujas funções são listadas acima, em um mesmo gráfico.
O modelo deste exercício terá:
- Três entradas, que são as três ondas senoidais dadas pelo enunciado;
- Um bloco “Mux”, que combinará os sinais das três ondas senoidais em um só sinal;
- Uma saída, que será um bloco “Scope”.
Neste exercício, veremos como alterar as propriedades do bloco “Mux”, para que ele tenha três entradas em vez de duas, e teremos que alterar as propriedades dos blocos “Sine Wave”, para criar as ondas senoidais dadas pelo enunciado.
Passo 2
A primeira coisa a fazer é criar as três ondas senoidais, começando por . Em um novo modelo, insira um bloco “Sine Wave”, da biblioteca “Sources”. Para ter acesso às propriedades de “Sine Wave”, clique duas vezes sobre o bloco:

Segundo a própria janela com os parâmetros do bloco, a onda senoidal gerada por “Sine Wave” tem esse formato:
![]()
A onda que queremos criar é , logo a amplitude é , a frequência é , a fase é e o é . Esses são os parâmetros destacados em vermelho acima. Note que não precisamos alterar nada nas propriedades, pois estes são os valores padrão.
Simplesmente feche a janela dos parâmetros e insira um segundo bloco “Sine Wave” ao modelo. Este segundo bloco gerará .
Perceba que ele tem uma fase diferente de , por isso, temos que acessar os parâmetros desse novo bloco que acabamos de inserir e alterar a fase da onda, no campo “Phase (rad)”, destacado abaixo:

Como dito acima, o valor padrão de “Phase (rad)” é , mas a onda tem fase igual a . Portanto, no campo “Phase (rad)”, troque por , como na imagem acima (o SIMULINK entende o como a constante ).
Clique em “OK” para registrar essa mudança. Por enquanto, nosso modelo tem dois blocos:

Passo 3
Vamos inserir um terceiro bloco “Sine Wave” para obter . Também teremos que mexer nas propriedades desse bloco, mas no campo “Frequency (rad/sec)”, destacado abaixo:

O padrão de “Sine Wave” é gerar uma onda senoidal com frequência , mas a onda tem uma frequência de . Portanto, troque no campo “Frequency (rad/sec)” o por, como na imagem acima.
Passo 4
Agora que já temos as três ondas senoidais, vamos inserir o bloco “Mux” para transformar os três sinais em um sinal só e termos as três ondas no mesmo gráfico. Vá à biblioteca “Signal Routing” e arraste o bloco “Mux” para o modelo.

Precisamos aumentar o número de entradas de “Mux”. Dê um duplo-clique sobre o bloco que você acabou de inserir, para ter acesso a suas propriedades:
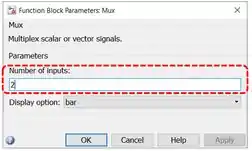
Na janela dos parâmetros de “Mux”, podemos definir o número de entradas do bloco. Altere esse valor para e você verá que aparecerá uma terceira setinha na lateral do bloco:

Conecte cada um dos blocos “Sine Wave” a uma entrada de “Mux”:

Passo 5
Vamos inserir a saída do modelo: um bloco “Scope”. Vá à biblioteca “Sinks”, arraste o bloco “Scope” para o modelo e conecte a saída de “Mux” à entrada de “Scope”:
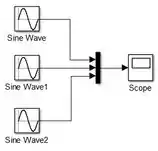
O modelo está pronto. Rode o programa e clique duas vezes sobre o “Scope” para visualizar o gráfico, que terá as três curvas do enunciado.
Resposta
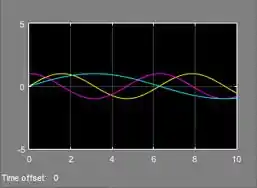
A onda é a curva amarela
A onda é a curva rosa
A onda é a curva azul
Exercício Resolvido #7
“Adaptado de Sistemas Dinâmicos I: Usando a ferramenta MATLAB, da USP, elaborado por Eduardo L. L. Cabral e Larissa Driemeier. Exemplo p. 81”
Considere o sistema massa-mola-amortecedor (MMA) abaixo:
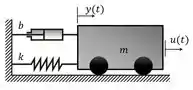
No SIMULINK, use o bloco “State Space” para calcular a resposta do sistema ao degrau unitário , considerando o sistema de equações no espaço de estados:
Onde é a posição da massa e é a velocidade (isto é, ). Considere as condições iniciais nulas () e simule o sistema por . Gere o gráfico da resposta e faça os ajustes necessários para melhorar a resolução do gráfico.
Passo 1
Neste exercício, vamos praticar a alterar algumas propriedades de simulação, como o tempo de simulação (o padrão no SIMULINK é e o enunciado pede simulação de ) e o tamanho mínimo e máximo do passo do algoritmo da simulação, para melhorar a resolução do gráfico. De quebra, vamos aprender como resolver equações no espaço de estados no SIMULINK.
O modelo deste exercício terá três blocos:
- A entrada do modelo será o bloco “Step”, para criar o sinal do degrau unitário ;
- Um bloco “State-Space” terá as equações do enunciado;
- A saída do modelo será um bloco “Scope”, para gerar um gráfico da solução das equações.
Após fazermos a simulação, vamos abrir o gráfico da solução e ver o que precisa ser ajustado.
Passo 2
Vamos começar construindo o modelo. Em um novo modelo, insira um bloco “Step”, indo na biblioteca “Sources” e arrastando-o para o modelo em branco.
O enunciado diz que o sinal de entrada é um degrau unitário e não especifica o instante em que ele começa. Como o “Step” por padrão é um degrau unitário, iniciando em segundo, não precisamos alterar propriedade alguma.
Vamos inserir o bloco “State-Space” no modelo para entrarmos com as equações no espaço de estados. Vá à biblioteca “Continuous”, encontre o bloco “State-Space” e arraste-o para o modelo:
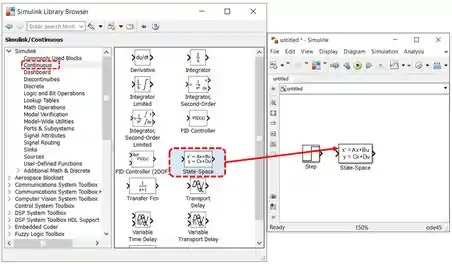
Para entrarmos com as equações do enunciado, dê um duplo-clique no bloco que você acabou de inserir, para ter acesso às propriedades:

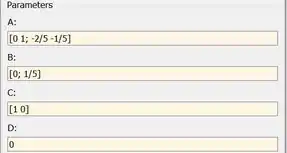
Para entrar as equações do enunciado, vamos alterar os campos destacados em vermelho, que é onde entramos as matrizes do sistema de equações de estado.
Para considerar as condições iniciais dadas pelo exercício, vamos alterar o campo destacado em azul (“Initial conditions”).
No topo da janela dos parâmetros de “State-Space”, há a indicação de quais são as matrizes a serem definidas nos campos destacados em vermelho:
![]()
Considerando que e , comparando com as equações dadas no enunciado, temos:
Logo, altere os campos onde entramos as matrizes para:

O enunciado diz que as condições iniciais são nulas. Isto quer dizer que:
Portanto, o campo “Initial conditions” será:
![]()
Clique em “OK” para registrar as alterações nos parâmetros e conecte o bloco “Step” ao bloco “Space-State”:
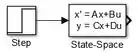
Passo 3
Vamos inserir a saída do modelo, um bloco “Scope”, e conectá-lo a “State-Space”:
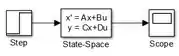
O modelo está pronto, agora precisamos ajustar o tempo de simulação de para . Na barra superior da janela do modelo, no campo onde podemos alterar o tempo de duração da simulação, destacado abaixo, troque por .
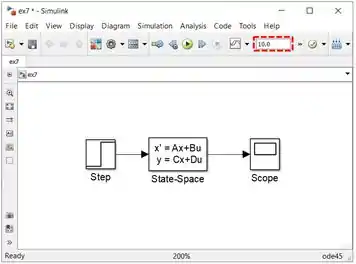
Execute a simulação e veja como ficou o gráfico (dê um “Autoscale” nele já, para ele ocupar toda a janela):

Passo 4
Dá pra perceber que a curva não está suave, tem umas partes pontiagudas e ela deveria ser mais “redondinha”. Para melhorar a aparência dela, vamos mudar dois parâmetros de simulação: o tamanho mínimo e máximo do passo do algoritmo da simulação.
Para acessar os parâmetros de simulação, clique sobre a engrenagem da barra superior da janela onde construímos os modelos, destacada em vermelho abaixo:
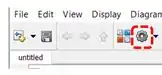
A janela “Configuration Parameters” aparecerá. Na seção “Solver”, estão os parâmetros que queremos ajustar para deixar a curva mais redonda (destacados em vermelho abaixo):
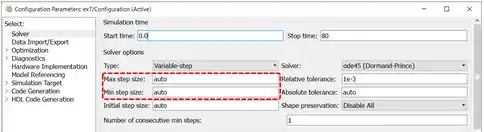
São os parâmetros “Max step size” (tamanho máximo de passo) e “Min step size” (tamanho mínimo de passo), que são calculados automaticamente por padrão. Para termos curvas com maior resolução, isto é, mais “redondinhas”, devemos usar valores de passo bem pequenos, da ordem de . Eu adotei os valores abaixo, mas você pode usar os valores que quiser.
![]()
Clique em “OK”, feche a janela do “Scope” e rode a simulação de novo, para ver como ficou o gráfico e se não ocorreu o fenômeno de “amnésia”:

Passo 5
É, teve uma amnésia bem grande aí. Para corrigi-la, vamos mudar a propriedade “Limit data points to last” do bloco “Scope”.
Para acessar as propriedades de “Scope”, na janela do gráfico com um pedaço faltando, clique na engrenagem destacada abaixo. Uma janela chamada “Scope parameters” se abrirá. Vá na aba “History”, onde tem a propriedade “Limit data points to last”, destacada abaixo:
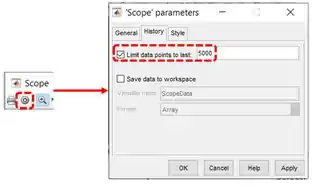
Devemos ser aumentar o valor do campo destacado em vermelho para corrigir o problema de faltar um pedaço da curva. Vamos mudar esse valor para , fechar a janela do “Scope” e rodar a simulação de novo.
Quando a execução do programa terminar, abra o gráfico novamente. Ele estará completinho e redondinho =D
Resposta

Exercício Resolvido #8
“Adaptado de Sistemas Dinâmicos I: Usando a ferramenta MATLAB, da USP, elaborado por Eduardo L. L. Cabral e Larissa Driemeier. Exercício 13.4.1, p. 86”
Considere o sistema massa-mola-amortecedor (MMA) abaixo:
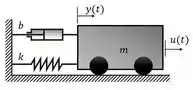
A modelagem dinâmica do MMA gera o sistema de equações no espaço de estados:
Onde é a posição da massa e é a velocidade (isto é, ).
No SIMULINK, use o bloco “State Space” para calcular a resposta a uma deflexão inicial de , sem ação externa (). Simule o sistema por , gere o gráfico da resposta do sistema e faça os ajustes necessários para melhorar a resolução do gráfico.
Passo 1
O exercício pede para gerarmos o gráfico da resposta do sistema MMA, usando as equações no espaço de estados. Para isto, contruiremos um modelo no SIMULINK com três blocos:
- A entrada do modelo será um bloco “Constant” que terá seu valor igual a , pois queremos ver somente o efeito da deflexão inicial. Em outras palavras, a entrada do sistema é ;
- Um bloco “State-Space” com as equações do enunciado;
- A saída do modelo será um bloco “Scope”, para gerar um gráfico da solução das equações, isto é, um gráfico de .
O tempo de simulação será de . Após fazermos a simulação, vamos abrir o gráfico da solução e ver o que precisa ser ajustado nos parâmetros de simulação e nas propriedades do “Scope” para melhorar a resolução do gráfico.
Passo 2
Vamos começar construindo o modelo. Em um arquivo do SIMULINK, insira um bloco “Constant”, pegando-o na biblioteca “Sources” e arrastando-o para o modelo em branco. Altere seu valor para , para indicar que não existe ação externa atuando sobre o sistema MMA.
Vamos inserir o bloco “State-Space” no modelo para entrarmos com as equações no espaço de estados. Vá à biblioteca “Continuous”, encontre o bloco “State-Space” e arraste-o para o modelo:

Dê um duplo-clique no bloco “State-Space” que você acabou de inserir para ter acesso às suas propriedades. É nelas que informamos as equações do enunciado:

Entramos as matrizes do sistema de equações de estado nos campos destacados em vermelho.
As condições iniciais são definidas no campo destacado em azul (“Initial conditions”).
No topo da janela dos parâmetros de “State-Space”, há a indicação de quais são as matrizes a serem definidas nos campos destacados em vermelho:
![]()
Considerando que e , comparando com as equações dadas no enunciado, temos:
Logo, altere os campos onde entramos as matrizes para:
O enunciado diz que há uma deflexão inicial de , mas não comentada nada de velocidade. Logo, podemos considerar que o bloco parte do repouso () e que o vetor no instante é:
Portanto, o campo “Initial conditions” será:
![]()
Clique em “OK” para registrar as alterações nos parâmetros e conecte o bloco “Constant” ao bloco “Space-State”:
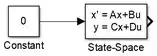
Passo 3
Para gerar o gráfico da resposta do sistema, vamos inserir a saída do modelo, um bloco “Scope”, e conectá-lo a “State-Space”:
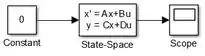
O modelo está pronto, falta só ajustar o tempo de simulação de para , no campo destacado abaixo:
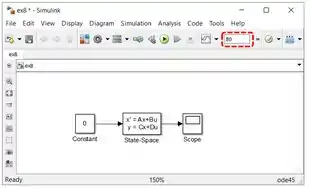
Execute a simulação e veja como ficou o gráfico. Já dê um “Autoscale” nele, para ele ocupar toda a janela:
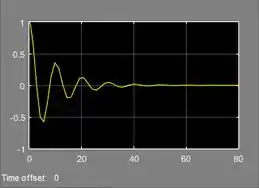
Passo 4
O gráfico não está com uma boa resolução, pois a curva está “pontiaguda” e meio truncada, em partes que deveriam ser mais arredondadas. Para aumentar a resolução do gráfico, vamos alterar o tamanho mínimo e máximo do passo do algoritmo da simulação.
Para acessar os parâmetros de simulação, clique sobre a engrenagem da barra superior da janela onde construímos os modelos, destacada em vermelho abaixo:
A janela “Configuration Parameters” abrirá, onde, na seção “Solver”, estão os parâmetros de passo que queremos ajustar para melhorar a resolução da curva (destacados em vermelho abaixo):

Os parâmetros “Max step size” (tamanho máximo de passo) e “Min step size” (tamanho mínimo de passo) são calculados automaticamente por padrão. Para termos curvas mais “redondinhas”, devemos usar valores de passo bem pequenos Eu costumo usar os valores abaixo, mas você pode usar os valores que quiser.
![]()
Rode a simulação novamente e veja como o gráfico ficou, para verificar se não há “amnésia”:
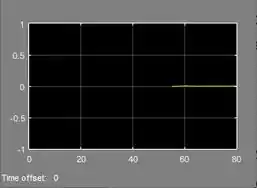
Passo 5
Estão faltando os primeiros do gráfico, logo, temos uma amnésia para corrigir. Para isto, vamos alterar a propriedade “Limit data points to last” do bloco “Scope”, cujas propriedades podem ser acessadas clicando na engrenagem destacada abaixo, na janela do gráfico com um pedaço faltando, isto é, na janela do “Scope”. O “Scope parameters” se abrirá. Vá à aba “History”, onde tem a propriedade “Limit data points to last”, destacada abaixo:
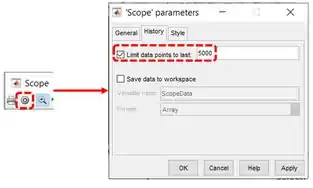
Para eliminar a amnésia, vamos aumentar o valor do campo destacado em vermelho. Altere esse valor para , feche a janela do “Scope” e rode a simulação de novo.
Abra o gráfico novamente e você verá que não tem mais amnésia e a curva estará “redondinha”.
Resposta
