Vetores e matrizes: criação
Produzido por Gustavo BarbosaTeoria
Definições básicas
Iae jovem, como você está?
Hoje vamos falar sobre Matrizes um elemento fundamental para o Matlab, bem como você já deve ter visto na matemática, matrizes na realidade é uma grande tabela com linhas e colunas que simbolicamente é representado por
Já o vetor é uma tabela com apenas linhas ou colunas, que é representado por ou
Bem, devo imaginar assim como foi comigo que isso é um pouco abstrato nos deixando meio aéreo

Mas não precisa ficar assim, vamos desmistificar isso juntos, ok?
Então vamos lá, imagine que você já chegou no final do mês e necessita comprar algumas coisas no mercado, aí tu verificaste tudo e monta a seguinte lista:
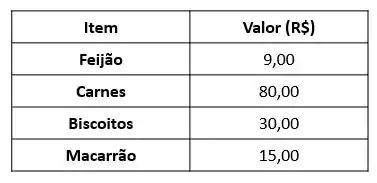
Observando bem essa pequena lista conseguimos observar que ela tem 5 linhas e 2 colunas, logo essa lista nada mais é do que uma matriz de 5 linhas e 2 colunas.
E se você for mais criterioso, ainda podemos dizer que essa lista é uma matriz composta por 2 vetores colunas cada um com 5 elementos.

Voltando ao assunto, você lembra da aula de variáveis? E que nós vimos que tem diversos tipos de variáveis?
Então, as matrizes e os vetores são similares e existem diversos tipos também e dependem unicamente dos elementos que os compõem, no exemplo anterior a primeira coluna de itens é um vetor do tipo string.
Na sua cabeça deve estar se passando, “ ok, ok, já entendi, mas como criar isso no Matlab? ”.
Pode ficar relaxado porque você vai saber disso tudo logo.
Criação de vetores e matrizes.
Bem pessoal, de uma forma prática as definições de vetores e matrizes que o Matlab segue são essas abaixo, de uma certa forma apenas precisamos saber das nomenclaturas. Pois, precisamos às vezes criar um vetor coluna e precisamos saber o que danado é isso, belezinha?

Agora que sabemos disso vamos lá aprender a criar essas coisas.
Criação de vetor
Basicamente a criação dessas coisas é bem prática, vamos realizar um exemplozinho para entender isso vamos pensar em um nome qualquer na minha cabeça vem o Ganef, olha só, imagina que o Ganef acabou de ganhar suas bolsas e está pensando em ir para um festão, porém precisa listar os valores em uma tabela.
Ai o ganef abriu o Matlab e digitou no command window:
bolsas=[100 150 120 350 230]
Ao da enter apareceu algo assim:

Só que o ganef não curtiu dessa forma aí ele quis deixar na forma de coluna, aí ele escreveu assim:
bolsas=
E apareceu algo assim:

Sendo assim, para criar um vetor basta colocar os valores entre os parênteses , se você colocar um espaçamento simples o Matlab irá criar um vetor linha.
Se colocar ponto e vírgula após os valores, ele cria um vetor coluna, belezinha?
Agora imagine se o ganeff precisasse escrever um vetor que começa do e vá até o variando de em , pelo método anterior você irá precisar escrever cada elemento dentro do vetor.

Mas isso é nada prático né? Relaxa, por isso iremos aprender um segundo método.
Segundo método: De uma forma prática a sintaxe para criar esse vetor é dada por:
Vamos fazer um exemplozinho, imagine que você precisa criar um vetor que ele conte de até variando de em .
Logo vamos pegar os dados, o é o valor inicial e o o valor final, vamos definir uma variável chamada de incremento, que é nada mais do que a diferença do elemento da frente em relação ao de trás, nesse caso o incremento é .
De uma forma mais clara o incremento é a variação, ok?
Então para escrevermos o vetor utilizamos a seguinte sintaxe
E se você escreveu tudo certinho deve mostrar algo mais ou menos assim:

Ou seja, qualquer vetor pode ser escrito a partir de valores, um valor inicial que nesse caso foi , um valor final que foi o e finalizando com uma variação.
Com a mesma sintaxe conseguimos criar qualquer vetor.
Criação de Matriz
Agora que vimos como criar os vetores, as matrizes se tornam mais intuitivas. Pois as matrizes podem ser vistas como composições de vetores.
Para não entrar em mais teorias, vamos voltar para um outro exemplo do Ganef, onde ele queria organizar em uma matriz os valores da , mas também os dias no qual ele recebeu esses valores, então:
Ganef já tem o seu vetor de bolsas:
Após isso, ele enumerou os dias da semana de recebimento, começando a segunda por 1 e assim por diante
E agora o Ganef deseja organizar isso numa tabela bonitinha então ele criou uma matriz
E a tabela do Matlab do ganef ficou assim:

Então para escrever uma matriz no Matlab apenas precisa escrever um vetor de linha e usa-se o ponto e vírgula ”;” e escreve o segundo vetor e assim sucessivamente, entende?
Bem galera, selecionamos uns exercícios bem legais para vocês treinarem e não deixem de treinar, na realidade programação é uma área que é muito mais prática do que algo teórico.
Ou seja, quanto mais você praticar, melhor irá ficar.
Bem, vamos ficar por aqui e até a próxima!!!!!!!!!! Iaeeee essa aula te ajudou? Responde Ai!
Criação de vetores e matrizes.
Exercícios Resolvidos
Exercício Resolvido #1
Elaboração Própria
Uma empresa opera em três regiões (Sul, Sudeste e Nordeste). Considere a seguinte informação sobre as suas vendas mensais (Janeiro a Dezembro) ao longo do último ano:
Sul: 15, 14, 14, 15, 14, 13, 12, 15, 17, 14, 14, 15;
Sudeste: 8, 6, 7, 7, 8, 7, 8, 8, 9, 8, 6, 7;
Nordeste: 4, 6, 4, 5, 6, 5, 3, 4, 7, 5, 6, 5.
Utilizando esses dados e seus conhecimentos monte uma planilha na janela de command window do Matlab.
Passo 1
Primeiramente precisamos criar os vetores com cada elemento assim como foi visto na aula de vetores e matrizes.
sul=[15; 14; 14; 15; 14; 13; 12; 15; 17; 14; 14; 15];
sudeste=[8; 6; 7; 7; 8; 7; 8; 8; 9; 8; 6; 7];
nordeste=[4; 6; 4; 5; 6; 5; 3; 4; 7; 5; 6; 5];
uma vez que foi criado os vetores podemos criar a matriz da seguinte forma:
Vendas=[sul sudeste nordeste]
Se escreveu tudo certinho deve aparecer algo mais ou menos assim:

Resposta
Ei, a resposta está no passo a passo :)
Exercício Resolvido #2
“Elaboração Própria”
Escreva as seguintes variáveis no matlab:
- Um vetor cuja as componentes são
- Um vetor que vá do até , apenas com os números pares
- Uma matriz M2,3 que varie de 1 a 6, onde a primeira linha contém os números ímpares e na segunda linha contém os números pares
Passo 1
A letra a) podemos responder escrevendo o vetor manualmente, pois é um vetor muito curtinho e com termos independentes.
Para escrever um vetor assim, vamos colocar os elementos dentro de colchetes e cada elemento separados apenas por espaços.
V=[1 4 9]
Se escreveu tudo certinho, deve mostrar algo do tipo:

Passo 2
Nessa letra b) vamos utilizar a segunda forma que aprendemos na aula.
Como nosso vetor só inclui os números pares, então vamos pegar números de 2 em 2, ou seja, o incremento é 2. Quando a gente tem um incremento constante entre os elementos do vetor, a gente pode escrever da seguinte forma:
V = 0 : 2 : 20
Aqui temos 3 valores à direita do V. O primeiro indica o primeiro termo do vetor (0), o segundo é o incremento (2) e o terceiro é o último termo do vetor (20). Essas 3 informações precisam ser separadas por dois pontos (:).
Se escreveu tudo certinho, vai aparecer algo mais ou menos assim:

Passo 3
Já aqui na terceira alternativa a forma de responder é similar ao que vimos na aula de vetores e matrizes.
Primeiramente criamos um vetor com os números impares que existem até o 6. Esse vetor vai ser a primeira linha da matriz.
impar = [1 3 5 ]
Agora criamos os vetores com os números pares, que formarão a segunda linha da matriz.
par = [ 2 4 6 ]
E agora, pra criar a matriz que a questão pede, é como fazer um vetor de vetores. A gente indica as linhas “impar” e “par” entre colchetes e na ordem correta.
M = [ impar ; par ]
Se tudo foi escrito certinho na sua tela deve aparecer algo assim:

Resposta
Ei, a resposta está no passo a passo :)
Exercício Resolvido #3
“Elaboração Própria”
Dadas as variáveis abaixo, escreva a transposta de cada uma.(lembrando que a transposta consiste em transformar linhas em coluna).
- O Vetor V=[1 2 3 4 5]
- A matriz M=[1 3 4 5; 4 5 6 3 ; 99 3 4 5]
Passo 1
Se você se lembrar da aula de vetores e matrizes, a letra a) é um vetor do tipo linha para transformá-lo em coluna precisamos trocar o espaçamento simples por ponto e vírgula, ou seja, se escrevermos o vetor do jeito que está no Matlab fica algo do tipo:

Reescrevendo em colunas temos algo do tipo:

Passo 2
Para resolver a questão b) podemos analisar a matriz como 3 vetores linhas e transformar cada um em coluna, logo:
V1=[1 3 4 5]
V2=[4 5 6 3 ]
V3=[99 3 4 5]
Agora tiramos a transposta de cada uma,
V1=[1;3;4;5]
V2=[4;5;6;3]
V3=[99;3;4;5]

E agora montamos a nova matriz com
W1=[1 4 99]
W2= [3 5 3]
W3= [4 6 4]
W4=[5 3 5]
Gerando os vetores:

Logo a matriz transposta se torna finalmente M=[W1;W2;W3;W4]

E podemos notar que realmente é a transposta apenas comparando com a matriz original.

Resposta
Ei, a resposta está no passo a passo :)
Exercício Resolvido #4
Elaboração Própria
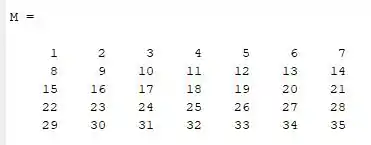
Crie uma matriz 5x7 onde a primeira linha seja formada pelos números 1; a segunda linha sejam os números ; a terceira linha os números de a , e assim por diante, até completar a matriz.
Passo 1
Se a gente analisar as sequências de números que o enunciado dá pra gente (as linhas da matriz), veremos que cada linha da matriz é uma sequência de 7 números de incremento 1.
Então podemos criar a primeira linha como um vetor. Como o incremento é constante e conhecemos o primeiro e o último número, fazemos assim.
Os 3 termos à direita são: o primeiro número do vetor (0), o incremento (1) e o último termo do vetor (7). E eles devem estar separados por dois pontos.
Do enunciado, também sabemos que o primeiro termo de uma linha (a partir da segunda) é igual ao último termo da linha anterior mais 1.
Uma vez que criamos as linhas da matriz podemos criar a matriz completa da seguinte forma:
No MatLab fica assim:
Resposta
Ei, a resposta está no passo a passo :)
Exercício Resolvido #5
Elaboração Própria
Declare a seguinte matriz A:

Use-a para:
a) criar um vetor linha de cinco elementos contendo os elementos da segunda linha de A.
b) criar um vetor linha de três elementos que contenha os elementos da quarta coluna de A.
c) criar um vetor linha de dez elementos que contenha os elementos da primeira e segunda linhas de A.
Passo 1
O problema pede que decomponhamos a matriz em alguns vetores, para isso vamos inserir primeiramente a matriz A no Matlab.
Agora basta criar a matriz

Uma vez que a matriz está pronta vamos resolver as alternativas
- Já inserimos a matriz decomposta assim justamente pensando em facilitar as respostas aqui, se você analisar a resposta da letra a) é justamente o vetor , logo V
- Os elementos da quarta coluna são os valores . Logo, o vetor se torna
- Para criar um vetor com 10 elementos com a primeira e segunda linha é uma tarefa fácil se caso você percebeu que a primeira linha é o V1 e a segunda o V2, pois se você percebeu isso esse vetor que pede na alternativa C é justamente o
Resposta
Ei, a resposta está no passo a passo :)
Exercício Resolvido #6
Elaboração Própria
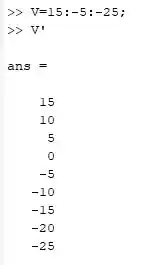
Crie um vetor coluna onde o primeiro elemento é 15, o último -25 e o decremento vale -5.
Obs: o vetor coluna pode ser criado a partir de um vetor linha transposto.
Passo 1
A questão em si é uma aplicação de criação de um vetor, para a transposição de um vetor basta colocar uma aspa simples nele, por exemplo:
Se no Matlab a variável é o vetor, o seu transposto basta escrever e o Matlab já transpõe o seu vetor, belezinha?
Então vamos lá resolver o probleminha.
Passo 2
Primeiramente precisamos criar o vetor de linha e para isso existem diversas formas.
Para simplificar o problema, deixar ele mais automático, vamos utilizar o segundo método que é aquele do incremento, ok?
Então para criar um vetor basta fazer assim:
Onde o primeiro número é o valor inicial, o segundo é o incremento e finalizamos com o último valor que é -25.
Sendo assim, o Matlab vai começar do 15 e vai diminuindo de -5 em -5 até chegar no -25.
E para transformar esse vetor de linha em um vetor coluna basta colocar e o Matlab já transpõem.
Passo 3
Se você digitou tudo certinho no Matlab, deve aparecer a seguinte informação para você:
Resposta
Ei, a resposta está no passo a passo :)
Exercício Resolvido #7
Elaboração Própria
Crie um vetor contendo elementos, onde o primeiro número é e o último . O espaçamento vale unidades. Em seguida, usando o segundo método, crie um outro vetor que contenha 8 elementos. Os quatro primeiros elementos do primeiro vetor devem ser os primeiros elementos de e os demais elementos desse vetor tem que ser os últimos elementos de .
Passo 1
A questão em si é uma aplicação de criação de dois vetores, primeiramente precisamos criar um vetor A e a partir dele criar um outro vetor qualquer utilizando os quatro primeiros e quatro últimos elementos.
Passo 2
Primeiramente vamos criar o vetor , ele começa no número 4 como informado pelo na questão e ele precisa ir até o valor de 49, segundo a questão ele varia de 3 em 3.
Sendo assim. Seguindo a sintaxe do segundo método temos que o vetor é criado da seguinte forma:
Agora vamos executar esse comando:

Para criar o segundo vetor vamos precisar dos quatro primeiros elementos do vetor A e finalizamos com os quatro últimos, sendo assim:
Executando o comando temos:
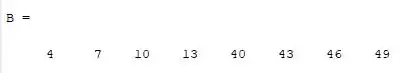
Resposta
Ei, a resposta está no passo a passo :)
Exercício Resolvido #8
Elaboração Própria
Crie uma tabela em Matlab onde calcula os valores do seno e do cosseno para os ângulos de
Passo 1
A questão em si é uma aplicação de criação de matrizes. Primeiramente precisamos implementar um vetor com os ângulos em radianos e depois disso calcular os valores dos senos e cossenos para assim montar uma matriz com seus valores, belezinha?
Passo 2
Primeiramente vamos criar o vetor , existe diversas formas de criar esse vetor mas vamos criar da forma mais simples que é inserindo os seus valores manualmente.
Sendo assim temos:
Agora vamos criar os vetores de seno e cosseno desse ângulo:
Agora que temos os vetores vamos criar a matriz:
Repara que dentro dos vetores, a gente separou os elementos com ponto e vírgula e na matriz separamos com espaços. Esses detalhes são importantes.
Se escreveu tudo certinho no Matlab deve mostrar algo mais ou menos assim:

Resposta
Ei, a resposta está no passo a passo :)