Exercícios de Módulo Math - Lista de Exercícios Resolvida
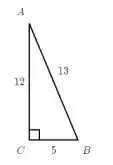
Questão 1
Elabore um programa que receba três valores reais, A, B e C, e calcule as raízes dessa equação do segundo grau. Para isso, deve usar obrigatoriamente uma função chamada bhaskara, escrita por você, que recebe os coeficientes como parâmetro. Além disso, a função deve calcular e retornar as duas raízes, reais ou complexas, dependendo dos coeficientes. O módulo utilizado deve ser chamado de m e deve existir apenas no escopo da função.
Exemplo 1:

Exemplo 2:
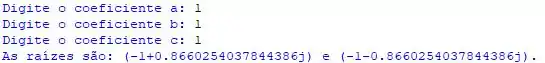
Questão 2
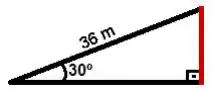
Uma rampa plana, de 36 m de comprimento, faz ângulo de 30° com o plano horizontal. Uma pessoa que sobe a rampa inteira eleva-se verticalmente quantos metros?
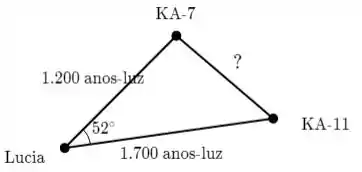
Questão 3
Ainda faltam dois sistemas solares para Lúcia visitar em sua viagem, mas sua espaçonave está com pouco combustível. O primeiro sistema, KA-7, está a 1.200 anos-luz (a.l.) de distância, enquanto o segundo sistema, KA-11, está a 1.700 a.l. Sua prioridade é visitar o sistema solar KA-7. Para determinar se ela também poderá visitar o KA-11, é preciso calcular a distância entre KA-7 e KA-11. Se Lúcia vê um ângulo de 52o entre KA-7 e KA-11, qual é a distância entre KA-7 e KA-11?
Questão 4
Escreva um programa que receba um número inteiro e exiba quantos dígitos o número tem. Para tal, seu programa deve usar uma abordagem puramente matemática. Seu programa não pode usar conversões de tipos ou laços de repetição.
Exemplo de funcionamento:

Questão 5
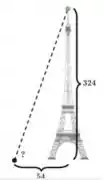
Um pequeno, porém, horrível, alienígena está no topo da Torre Eiffel (que tem 324 metros de altura) e ameaça destruir a cidade de Paris! Um agente da MIB está no nível do chão, a 54 metros da Torre Eiffel, mirando sua arma a laser no alienígena. Em que ângulo, em graus, o agente deve disparar a arma?
Questão 6
Possuo 4 bolas amarelas, 3 bolas vermelhas, 2 bolas azuis e 1 bola verde. Pretendo colocá-las em um tubo acrílico translúcido e incolor, onde elas ficarão umas sobre as outras na vertical. De quantas maneiras distintas podemos formar essa coluna de bolas?
Ver solução completa