Mecanismo de Condutância
Teoria
Fala aí galera! Partiu dar aquela estudada em mecanismo de condutância, beleza? Vamo que vamo!
Bom, pra chegar aqui a gente já entendeu tudo sobre condutância, lei de condutância e etc… né?
Show! Mas antes da gente ver a equaçãozinha que vamos usar, é muitoooo importante saber de alguns conceitos que nos leva até ela!
Atrito ou Arraste do Solvente
O atrito é nosso velho conhecido lá da física… E aqui ele vai ter exatamente o mesmo significado, ok? É uma força que tenta impedir o movimento, no nosso caso aqui esse movimento é dos íons… Tranquilo?
Quando temos uma ddp aplicada, os íons são acelerados para entrar em movimento e para conseguir ele precisa vencer o atrito. Se a gente estiver em um meio viscoso estacionário, essa força de atrito pode ser calculada pela Lei de Stokes da seguinte forma:
Efeito de Relaxação
Olha só, nosso amigo Debye-Huckel em uma teoria que diz o seguinte: o íon tem uma nuvem iônica em volta dele que é simétrica, beleza? A carga dessa nuvem é igual e oposta a carga do íon central, quando a gente aplica uma ddp na solução, o íon central vai se mover em direção ao eletrodo que tem a carga oposta a dele… assim olha:
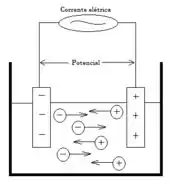
Mas lembra da nuvem iônica? ela não vai ser atraída pelo eletrodo, já que suas cargas serão iguais… Então a nuvem que tinha uma simetria esférica vai se deformar, por causa da força de repulsão, mas isso vai gerar um acúmulo de carga de um lado que vai durar algum tempo até que a nuvem volte ao seu estado normal, esse tempo é o tempo de relaxação.
Essa deformação na nuvem que é criada por um tempo vai retardar o movimento do íon que está indo para o eletrodo, isso faz com que a condutância dele seja reduzida, e é esse efeito que chamamos de efeito de relaxação.
Efeito eletroforético
Esse efeito aqui é mais uma prova daquela nuvem iônica que falamos ali em cima. Lembra de interações intermoleculares? Então, a interação do íon com o solvente é do tipo íon-dipolo, isso quer dizer que quando o íon está se movendo ele vai arrastando o solvente juntinho com ele… Maasss a nuvem iônica faz o solvente ser arrastado na direção contrária e assim faz nosso íon se mover mais lento.
Além disso, o efeito eletroforético, impede que o solvente seja tratado como um meio viscoso e estacionário, né? Porque a gente acabou de ver que ele vai se mover também!
Show de bola! Esses conceitos aí foram super importantes, porque foi através deles que Debye e Huckel desenvolveram equações que representam as forças externas que atuam sobre o íon central, e em 1926 o Lars Onsager aperfeiçoou todo o estudo e chegou nessa equaçãozinha aqui:
Esse e aí são as constantes de Onsager, elas são tabeladas e esse é a nossa concentração.
Essa equação se baseia em uma dissolução completa… E se não for completa? Bom, nos casos que temos eletrólitos fracos os efeitos que vimos antes, de relaxação e eletroforéticos, vão ser desprezados, e aí é só usar a equação de condutividade molar, que vimos na parte anterior, a equação de Kohlrausch, só pra relembrar:
E no caso de uma dissociação incompleta? Aí a gente usa uma outra equação. Esse tipo acontece em eletrólitos univalentes em soluções muito diluídas e a gente usa essa equação aqui:
Ela é conhecida como equação de Debye-Huckel-Onsager, mostra pra gente que a condutividade molar em função da raiz da concentração, é uma função que depende da natureza do solvente e da temperatura.
Belezinha? Agora que vimos toda essa parte de mecanismo de condutância vamos partir para fixar esse conteúdo com exercícios?
Atrito ou Arraste do Solvente
Efeito de Relaxação
Efeito eletroforético
Exercícios Resolvidos
Exercício Resolvido #1
Cadernos de Físico-Química Eletroquímica - Professora: Sonia Regina
Como varia a condutância dos eletrólitos fracos e fortes com a diluição?
Passo 1
Fala aí! Vamos consolidar nossos conhecimentos com uma questãozinha teórica, beleza?
Bom, pra responder essa questão precisamos dar uma relembrada lá na nossa teoria. Quando trabalhamos com eletrólitos fortes, temos a influência de efeitos como o de relaxação e eletroforético, neste caso teremos uma diluição completa e para calcular a condutância usamos a equação que usa as constantes de Onsager, essa aqui, olha só:
Já quando estamos trabalhando com eletrólitos fracos, podemos desprezar os efeitos de relaxação e eletroforético, por causa das distâncias interiônicas que eles apresentam. Nesse caso então a condutância é calculada pela equação de Kohlrausch, desse jeito:
Tranquilo? Show de bola! Conseguimos!
Resposta
Passo 1.
Exercício Resolvido #2
Cadernos de Físico-Química Eletroquímica - Professora: Sonia Regina
Como varia a condutância iônica com a temperatura?
Passo 1
Vamos continuar nosso processo de fixar conhecimento? Partiu!
Essa questão aí precisa que a gente fique atento na teoria que estudamos… Nós vimos que a condutância vai mudar de acordo com o tipo de dissociação, se ela é completa ou incompleta. No caso das dissociações completas, olhando para a equação da condutância a gente até acha que não depende da temperatura, né?
Mas tá ligado nesse e esse aí, que são as constantes de Onsager, elas são tabeladas para as diferentes substância e são dependentes da constante dielétrica do solvente, da viscosidade e da temperatura, beleza? Então é dessa forma que se dá a dependência no caso de dissociações completas.
Nas dissociações incompletas, a dependência da temperatura é mais explícita na equação da condutância, olha só:
Dá pra gente ver que elas são inversamente proporcionais, né? Quanto maior a temperatura que vamos trabalhar menor será a condutância que teremos.
Show de bola! Conseguimos!
Resposta
Passo 1.
Exercício Resolvido #3
Elaboração própria.
Encontre a condutividade molar de uma solução de de Cloreto de potássio saturada em água a 25°C, utilizando a equação de Debye e Huckel.
Dados:
Água a 25°C :, e
a 25°C :
Passo 1
Vamos mostrar pra essa questão do que a gente é capaz! Ela quer que a gente encontra a condutividade molar, usando essa equaçãozinha aqui:
Temos todos os dados, vamos lá então!
Show de bolinhas! Tudo pronto!
Resposta
Exercício Resolvido #4
Cadernos de Físico-Química Eletroquímica - Professora: Sonia Regina
Explique porque ocorrem desvios à equação de Onsager.
Passo 1
Vamos analisar a equação de Onsager e verificar o porquê de ocorrer desvios, beleza?
Bom, vamos começar lembrando que a teoria de Debye, Huckel e Onsager faz diversas considerações para os tipos de diluição e tal, mas aqui ele quer saber sobre os desvios que a equação sofre quando não trabalhamos com soluções muito diluídas e não trabalhamos com eletrólitos uni-univalentes, ok?
Esses desvios acontecem porque nesse caso ocorre formação de pares iônicos e eles são eletricamente neutros, então não contribuem para a condutância. Sendo assim, eles causam uma diminuição na condutância. No caso de solventes de baixa constante dielétrica, não necessariamente são pares iônicos, podem ser tripletos, ou seja, a concentração pode ser grande e formar íons-triplos e aí nesse caso aqui, eles contribuem para o transporte de corrente, então aumentam a condutância, beleza?
Mandamos bem!
Resposta
Passo 1.
Exercício Resolvido #5
Cadernos de Físico-Química Eletroquímica - Professora: Sonia Regina
Para um eletrólito uni-univalente a equação de Onsager se escreve (a 25°C)
Calcule a condutância equivalente das soluções de cujas concentrações são dadas a seguir e compare com os valores experimentais obtidos a 25°C.
Passo 1
Fala aí! Pra começar precisamos buscar em uma fonte segura a condutividade molar do , ok? Vamos encontrar aproximadamente:
Agora vamos substituir cada valor de concentração na equação que foi daa pra gente, teremos o seguinte:
Para :
Para :
Para :
Para :
Para :
Passo 2
Agora que fizemos todas as continhas, observando o resultado, vemos que quanto maior a concentração, menor foi a nossa condutância equivalente, né?
E comparando aos dados experimentais, tivemos resultados muito parecidos para concentrações menores… E isso pode ser explicado por causa dos desvios da equação de Onsager.
Show de bolinhas!
Resposta
