Mobilidade Iônica
Produzido por Marcelo BrillantinoTeoria
E aí? Tudo joinhas? Vamos para mais um assunto que vai mudar nossa vida!!
Quando a gente fala de mobilidade, já imaginamos algo se movendo, né? E se ela é iônica, podemos dizer que estamos falando do movimento de íons, Exatamenteee!!
Chega aí e dá uma olhadinha nessa figura:
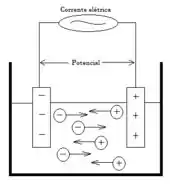
Estamos vendo íons em uma solução, sob ação de um campo elétrico, eles ficam migrando através da solução, em movimento aleatório. Os cátions são acelerados em direção ao eletrodo negativo e os ânions em direção ao eletrodo positivo.
A corrente no circuito depende do número de íons que se aproxima dos eletrodos, por unidade de tempo. Se o eletrodo que usamos tem uma área , os íons terão uma velocidade média em um intervalo de tempo , beleza?
O movimento sofre a ação de duas forças diferentes. A primeira é a força elétrica, por causa do campo elétrico que é aplicado, ela pode ser calculada assim:
Esse é o nosso íon que a gente pode considerar como uma esfera, tendo carga , ficando dessa forma:
E a segunda força é o atrito, por causa da viscosidade do meio que nossos íons estão se movendo, ok? E não podemos esquecer que ela vai ser orientada na direção contrário do deslocamento, será dada por:
Esse é o coeficiente de viscosidade da solução, o é o raio do íon e o a velocidade de migração do íon… Tranquilo?
Usando a relação dessas duas forças a gente tem a definição matemática da mobilidade iônica:
Nessa equação a gente ainda pode relacionar com o conceito de condutividade molar do íon, pela equação:
Esse é a constante de Faraday, beleza? Agora se a gente substituir isso na equação da mobilidade iônica vamos ter:
Número de Transporte
Ele é a fração da corrente total que é transportada pelo íon. As frações de corrente serão dadas:
E eles vão obedecer a essas relações aqui:
e
O número de transporte de cátions e de ânions não são iguais por causa da diferença de velocidade entre as duas espécies iônicas na solução, ok? Além disso, o número de transporte de cada espécie iônica é proporcional às mobilidades dos íons em uma solução infinita, quando a ionização é total, vamos ter que:
Esses são os números de transporte a diluição infinita e esses e , são as mobilidades iônicas a diluição infinita.
E se a gente correlacionar isso com as condutividades molares limites dos íons, vamos ter o seguinte, olha só:
Bom, vimos muitas equaçõezinhas agora precisamos ver a aplicação disso tudo, né?

Número de Transporte
Exercícios Resolvidos
Exercício Resolvido #1
Cadernos de Físico-Química Eletroquímica - Professora: Sonia Regina
Defina número de transporte e mobilidade iônica.
Passo 1
Fala aí! Vamos consolidar nossos conhecimentos com uma questãozinha teórica, beleza?
Começaremos definindo o número de transporte, ok? Ele indica pra gente a fração da corrente total que é transportada pelo íon, o positivo e o negativo.
Agora vamos a definição de mobilidade iônica! Ela representa o deslocamento médio, aleatório, dos íons em solução sob a influência de um campo elétrico.
Prontinho! Já definimos tudo!
Resposta
Passo 1.
Exercício Resolvido #2
Unicamp - Lista de Exercício - QG100
A mobilidade do íon em solução aquosa é a . A diferença de
potencial entre dois eletrodos na solução é de . Se os eletrodos estão a de distância, qual é a velocidade de deriva dos íons devido a este potencial?
Passo 1
Opa! Partiu fazer exercícios! Esse enunciado pediu pra gente encontrar a velocidade de deriva dos íons de , ok? Os que ele nos deu foi o seguinte:
Podemos usar a seguinte relação:
Ops! Mas a gente não tem o campo elétrico!

Relaxa! Temos como achar ele, assim olha:
Colocando isso na nossa equação vamos encontrar a velocidade, desse jeito:
Conseguimos! Show de bola!
Resposta
Exercício Resolvido #3
UFPR - Condutividade - Físico-Química
Qual a mobilidade de um íon de que está entre dois eletrodos separados por com , , e ().
Passo 1
Vamos lá resolver essa questãozinha juntos! O enunciado pediu pra gente encontrar a mobilidade iônica do , né? Podemos achar assim, olha só:
Vamos ficar atentos nas unidades, beleza?
Além disso, precisamos lembrar que o … Opa! Temos todos os termos, partiu encontrar a mobilidade!
Prontinho! Encontramos a mobilidade iônica!
Resposta
Exercício Resolvido #4
UFF - Físico-Química V - 3ª Lista de Exercícios - Professor Raphael Cruz
A , a condutância equivalente à diluição infinita para o nitrato de prata é igual a . Qual a mobilidade do íon ? O número de transporte do íon vale .
Passo 1
Fala aí! Partiu resolver isso aí juntos! O enunciado pediu pra gente encontrar a mobilidade iônica do , e nos deu o seguinte:
Hum… Como vamos fazer para encontrar a mobilidade aqui? Tem uma informação muito importante no nosso enunciado, olha só, lá tá dizendo que estamos trabalhando com diluição infinita, pegou o bizu?
Quando a gente trabalha com esse tipo de diluição é válida a seguinte relação para encontrar a condutância iônica:
E a mobilidade iônica pode ser calculada assim:
E esse é a constante de Faraday, que já é nossa conhecida, sendo:
Passo 2
Opa! Então isso quer dizer que podemos encontrar a mobilidade iônica, se tratando de uma diluição infinita, como:
Vamos substituir nossos dados então:
Conseguimos!
Resposta
Exercício Resolvido #5
UFF - Físico-Química V - 3ª Lista de Exercícios - Professor Raphael Cruz
Qual a relação entre mobilidade iônica e condutância equivalente iônica?
Passo 1
Questão teórica pra gente testar nosso aprendizado! O enunciado quer saber a relação entre mobilidade iônica e condutância equivalente… Bom, vamos lembrar das relações que nós vimos até aqui, beleza?
Podemos verificar essa relação quando estamos trabalhando com diluição infinita, pois podemos verificar a equação:
E ela nos mostra que a mobilidade iônica é diretamente proporcional a condutância, ou seja, se a gente aumenta a condutância teremos uma maior mobilidade… Bom, vamos pensar… Isso faz todo sentido, não é mesmo? Sendo a mobilidade o movimento de íons, quanto maior esse movimento maior será nossa condutância!
Arrasamos!
Resposta
Passo 1.