1.2 Deduza a equação entre a pressão e a massa específica, , de um gás perfeito de massa molar . Verifique graficamente o resultado com os seguintes dados referentes ao éter dimetílico, a 25°C, mostrando que o comportamento de gás pefeito ocorre nas pressões baixas. Estime a massa molar do gás.

Vamos primeiro pegar a equação do gás perfeito:

Substituindo:

E substituindo, também, chegamos a:

Agora vamos com calma e paciência, ta bem??

Pensa comigo... O éter dimetílico não é um gás perfeito, né? Então é um gás real. Vamos usar a equação do virial:

Chegamos uma equação que tem e . Vamos plotar num gráfico e .

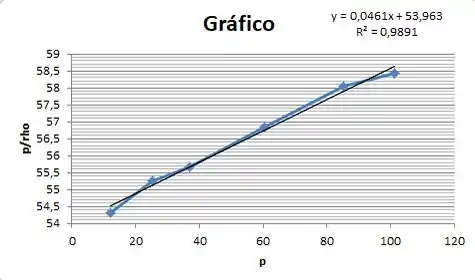
Bom... como se aproxima de uma reta (tem próximo de 1), podemos desprezar, então, os termos de ordem superior e ficamos com:

Repara quando quando o do lado direito da equação for tendendo a zero, ficamos com:

Que nada mais é, a equação do gás perfeito.

Pra estimar a massa molar comparamos a equação que achamos na regressão linear:

Usando e :