Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Atkins - Fisico-Quimica - Vol. 1- Ed: 8º - Capítulo 9.Problemas Numéricos - Ex. 4

Calcule as energias dos quatro primeiros níveis de rotação da molécula de H 127 I livre para girar em três dimensões, com o momento de inércia I = μ R 2 , com μ = m H m I / ( m H + m I ) e R = 160   p m .

Passo 1

Simbora!

Da equação 9.53, teremos:

E = l l + 1 ℏ 2 2 I = l l + 1 ℏ 2 2 m r 2

Note que aqui, temos que:

I = m R 2

sendo que esse m quando formos iniciar nossos cálculos, será dado por:

1 m = 1 m H + 1 m I

Assim, teremos, lembrando que ℏ = 1,055 × 10 - 34 J s que,

E = l l + 1 1,055 × 10 - 34 J s 2 2 1,6605 × 10 - 27 k g 160 × 10 012   m 2 1 1,008 + 1 126,90

E = l ( l + 1 ) ( 1,31 × 10 - 22 J )

Passo 2

A energia pode ser expressada pelas frequências equivalentes,

ν = E h = 1,509 × 10 33 J - 1 s - 1 E

Assim, ao colocar valores de l , teremos a seguinte tabelinha:

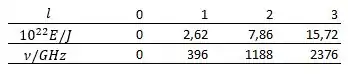
Resposta

Ei, a resposta está no passo a passo :)

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Para o átomo de hidrogênio, à medida que n aumenta, o espaçamento dos níveis de energia adjacentes em um diagrama de nível de energia aumenta ou diminui?