Enunciado
Química - Fundamentos de química analítica, Skoog- Ed: 8º - Capítulo 14.Questões e Problemas - Ex. 47
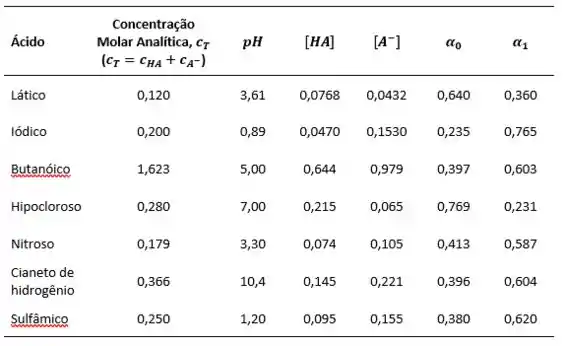
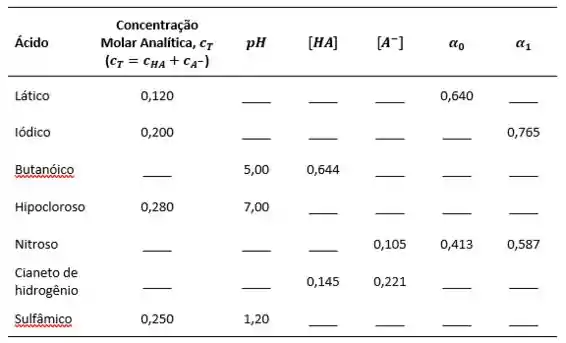
Complete com os dados que faltam na tabela a seguir.
Passo 1
Olá galerinha, tudo bem com vocês? Antes de iniciarmos este exercício vamos relembrar algumas equações.
A equação de é a fração da concentração total do ácido que permanece não dissociada, e é dada pela equação:
E é a fração dissociada:
Além disso sabemos que:
Para encontrarmos o pH, utilizamos a seguinte equação:
E a equação da concentração de equilíbrio do ácido não dissociado, e dissociado, respectivamente:
Sabendo disso, vamos lá! Para o ácido lático, temos os dados:
;
.
E pelo Apêndice 3, encontramos a constante de dissociação ácida do ácido lático:
Então:
Rearranjando a equação de para obtermos o valor da concentração de :
Com este valor conseguimos encontrar o valor do pH:
Passo 2
Para o ácido iódico, temos os dados:
;
.
E pelo Apêndice 3, encontramos a constante de dissociação ácida do ácido iódico:
Então:
Rearranjando a equação de para obtermos o valor da concentração de :
Com este valor conseguimos encontrar o valor do pH:
Para o ácido butanóico, temos os dados:
;
.
Para este ácido iremos começar calculando a concentração de :
E pelo Apêndice 3, encontramos a constante de dissociação ácida do ácido butanóico:
Então:
Passo 3
Para o ácido hipocloroso, temos os dados:
;
.
Agora iremos calcular a concentração de :
E pelo Apêndice 3, encontramos a constante de dissociação ácida do ácido hipocloroso:
Então:
Para o ácido nitroso, temos os dados:
;
;
.
E pelo Apêndice 3, encontramos a constante de dissociação ácida do ácido nitroso:
Então:
Rearranjando a equação de para obtermos o valor da concentração de :
Com este valor conseguimos encontrar o valor do pH:
Passo 4
Para o cianeto de hidrogênio, temos os dados:
;
.
E pelo Apêndice 3, encontramos a constante de dissociação ácida do cianeto de hidrogênio:
Para o cianeto iremos começar calculando a concentração molar analítica pela seguinte equação:
Então temos:
Rearranjando a equação de para obtermos o valor da concentração de :
Com este valor conseguimos encontrar o valor do pH:
Para o ácido sulfâmico, temos os dados:
;
.
E pelo Apêndice 3, encontramos a constante de dissociação ácida do ácido sulfâmico:
Para este ácido iremos começar calculando a concentração de :
Então:
Até mais pessoal! Espero que tenham gostado da resolução.
Resposta
