- Confirme, utilizando a trigonometria, que os dipolos das três ligações de uma molécula trigonal piramidal, , não se cancelam e que a molécula é polar;
- Mostre que os dipolos das quatro ligações de uma molécula tetraédrica, , se cancelam e que a molécula é apolar.
Passo 1
Bom galera, o que é dipolo?
As moléculas diferentes possuem eletronegatividade diferente, consequentemente, elas atraem elétrons com maior ou menor força. Quando formando polos negativos e positivos.
Na molécula trigonal piramidal, , a estrutura é:
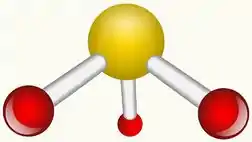
Considerando que cada ligação com B seja um vetor, nós teremos 3 vetores apontados para baixo, formando um vetor resultante.
Até aqui tudo certo?
Se temos esse vetor pontado para baixo, nós teremos ali a formação de um polo, ou seja, molécula polar.
Passo 2
Quando a molécula é tetraédrica,
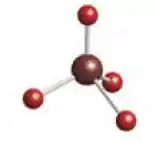
Aqui nós temos, assim como no passo 1, um vetor resultante apontado para baixo e um para cima, já que temos um átomo nesta posição. Sendo assim, não há a formação de polos.
Tudo bem?
Resposta
Ei, a resposta está no passo a passo :)