Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Química - Atkins - Fisico-Quimica - Vol. 1- Ed: 8º - Capítulo 12.Problemas Numéricos - Ex. 7

Construa a tabela de multiplicação das matrizes do spin de Pauli, σ , e da matriz unitária 2 × 2 :

σ x = 0 1 1 0 ,                     σ y = 0 - i i 0 ,                   σ z = 1 0 0 - 1 ,                       σ 0 = 1 0 0 1

As quatro matrizes formam um grupo com relação à operação de multiplicação?

Passo 1

Eis que a álgebra linear vem se misturar com a físico-química hahahaha

Mas vamos lá matar essa questão! Temos as matrizes do spin de Pauli e a matriz unitária (a querida matriz identidade):

σ x = 0 1 1 0 ,                     σ y = 0 - i i 0 ,                   σ z = 1 0 0 - 1 ,                       σ 0 = 1 0 0 1

E queremos construir sua tabela de multiplicação, certo?

“Hã? Do que você ta falando?”

Basicamente, vamos preencher essa tabela aqui, de acordo com as multiplicações entre cada uma dessas matrizes:

Vamos lá??

Passo 2

Vamos começar multiplicando cada matriz por ela mesma, ok?

Temos, para σ x

σ x ² = 0 1 1 0 × 0 1 1 0

σ x 2 = 0.0 + 1.1 0.1 + 1.0 1.0 + 0.1 1.1 + 0.0

σ x 2 = 1 0 0 1

Agora para σ y :

σ y ² = 0 - i i 0 × 0 - i i 0

σ y 2 = 0.0 + ( - i ) . i 0 . - i + - i . 0 i . 0 + 0 . i i - i + 0.0

Por propriedade de número complexo, temos i . i = - 1 e i . - i = 1

σ y 2 = 1 0 0 1

Para σ z :

σ z ² = 1 0 0 - 1 × 1 0 0 - 1

σ z 2 = 1.1 + 0.0 1.0 + 0 . ( - 1 ) 0.1 + - 1 . 0 0.0 + - 1 . ( - 1 )

σ z 2 = 1 0 0 1

Finalmente, para σ 0 :

σ 0 ² = 1 0 0 1 × 1 0 0 1

σ 0 2 = 1.1 + 0.0 1.0 + 0.1 0.1 + 1.0 0.0 + 1.1

σ 0 2 = 1 0 0 1

Cada uma das matrizes ao quadrado formou a própria matriz identidade

Também temos que lembrar que qualquer matriz A multiplicada pela matriz identidade σ 0 , dá a própria matriz A , certo?

Então, até o momento, nossa tabela ta assim:

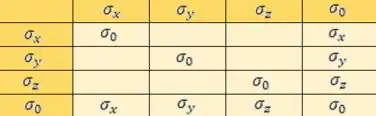
Passo 3

Agora vamos multiplicar as matrizes entre si

σ x   e   σ y

σ x . σ y = 0 1 1 0 × 0 - i i 0

σ x . σ y = 0.0 + 1 . i 0 . - i + 1.0 1.0 + 0 . i 1 . - i + 0.0

σ x . σ y = i 0 0 - i = i . 1 0 0 - 1 = i . σ z

σ y   e   σ x

σ y . σ x = 0 - i i 0 × 0 1 1 0

σ y . σ x = 0.0 + - i . 1 0.1 + - i . 0 i . 0 + 0.1 i . 1 + 0.0

σ y . σ x = - i 0 0 i = - i . 1 0 0 - 1 = - i . σ z

σ x   e   σ z

σ x . σ z = 0 1 1 0 × 1 0 0 - 1

σ x . σ z = 0.1 + 1.0 0.0 + 1 . ( - 1 ) 1.1 + 0.0 1.0 + 0 . ( - 1 )

σ x . σ z = 0 - 1 1 0

Usando as propriedades de números complexos lá do passo 1, podemos escrever isso assim:

σ x . σ z = 0 i ² - i ² 0 = - i . 0 - i i 0 = - i . σ y

σ z   e   σ x

σ z . σ x = 1 0 0 - 1 × 0 1 1 0

σ z . σ x = 1.0 + 0.1 1.1 + 0.0 0.0 + - 1 . 1 0.1 + - 1 . 0

σ z . σ x = 0 1 - 1 0

Usando as propriedades de números complexos lá do passo 1, podemos escrever isso assim:

σ z . σ x = 0 - i ² i ² 0 = i . 0 - i i 0 = i . σ y

Agora que calculamos todas as multiplicações envolvendo σ x , nossa matriz está assim:

Agora só falta σ y . σ z e σ z . σ y , bora!

Passo 4

Temos:

σ y   e   σ z

σ y . σ z = 0 - i i 0 × 1 0 0 - 1

σ y . σ z = 0.1 + - i . 0 0.0 + - i . ( - 1 ) i . 1 + 0.0 i . 0 + 0 . ( - 1 )

σ y . σ z = 0 i i 0 = i . 0 1 1 0 = i . σ x

σ z   e   σ y

σ z . σ y = 1 0 0 - 1 × 0 - i i 0

σ z . σ y = 1.0 + 0 . i 0.0 + - 1 . i 0.0 + - 1 . i 0 . - i + - 1 . 0

σ z . σ y = 0 - i - i 0 = - i . 0 1 1 0 = - i . σ x

Então, nossa tabela de multiplicação fica assim:

Passo 5

Agora vamos analisar se as 4 matrizes formam um grupo com relação à operação de multiplicação

A primeira regra para que isso aconteça é que a multiplicação entre cada um dos termos da tabela de multiplicação resulte em alguma das 4 matrizes dadas

Então vamos imaginar o grupo K = σ x ,   σ y ,   σ z ,   σ 0 ,   - i . σ z ,   i . σ z ,   - i . σ y ,   i . σ y ,   - i . σ x ,   i . σ x

Temos

σ x × σ x = σ y × σ y = σ z × σ z = σ 0 ∈ K

O problema ta quando multiplicamos esses termos:

i . σ x ×   i . σ x = i ² σ x ² ∉ K

σ x × σ y × σ z = i σ 0 ∉ K

Ou seja, alguns termos, quando se multiplicam, resultam em valores que não estão dentro do grupo P

Poxa, então os termos nossa tabela de multiplicação não formam um grupo fechado nessa operação, beleza?

Mas enfim, acabamos galeraaa

Resposta

Não formam um grupo com relação à multiplicação

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

A transição A 1 g → E 2 u é proibida ou não, como transição de dipolo elétrico numa molécula D 6 h ?
Identifique os grupos de simetria das seguintes moléculas (a) HF, (b)IF7, (c) XeO2F2, (d) Fe2(CO)9, (e)C8H8, (f) C4H4F4.
Imagine a molécula NO3- do C3V. Há algum orbital do átomo de N central que possa ter superposição não-nula com essa combinação não-nula com a combinação 2 p x A - p x B - p x ( c ) dos três átomos de
A molécula CCl4, pertence ao grupo Td. Dê os elementos de simetria do grupo e localize-os na molécula.
Com as propriedades de simetria determine se a integral dada a seguir é ou não necessariamente nula em uma molécula com simetria D 6 h .