Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Química - Fundamentos de química analítica, Skoog- Ed: 8º - Capítulo 18.Questões e Problemas - Ex. 18

Se as seguintes meias-células forem o eletrodo do lado direito de uma célula galvânica, com o eletrodo padrão de hidrogênio à esquerda, calcule o potencial da célula. Se a célula fosse colocada em curto circuito, indique se os eletrodos mostrados se comportariam como ânodo ou cátodo.

  1. N i | N i 2 _ ( 0,0943   m o l / L ) .

  2. A g |   A g I ( s a t u r a d o ) ,   K I ( 0,0922   m o l / L )

  3. P t , O 2 ( 780   t o r r ) ,   H C l ( 1,50 × 10 - 4   m o l /   L ).
  4. P t |   S n 2 + ( 0,0944   m o l   / L ) ,   S n 4 + ( 0,350   m o l   L _ 1 ) .

  5. A g   |   A g ( S _ 2 O _ 3 )   ( 0,00753   m o l   / L ) ,   N a 2 S 2 O 3   ( 0,1439   m o l / L )

Passo 1

Nesta tarefa, precisamos determinar se o eletrodo é cátodo ou ânodo.

O potencial da célula galvânica, ou a tensão da célula, é a diferença entre os potenciais do eletrodo de redução padrão do cátodo e do ânodo:

E = E c a t o d o - E a n o d o

Utilizando os dados dos valores dos potenciais de eletrodos redutores padrão, que podem ser encontrados na tabela, é possível calcular a tensão de qualquer célula galvânica.

Os eletrodos, o ânodo (negativo) e o cátodo (positivo), diferem entre si no tipo de reação que ocorre neles. O anodo é o eletrodo no qual a reação de oxidação sempre ocorre, e o cátodo é o eletrodo no qual a reação de redução sempre ocorre.

O eletrodo da direita é o eletrodo de hidrogênio padrão. O potencial de eletrodo de redução padrão de um eletrodo de hidrogênio padrão é por acordo zero em todas as temperaturas.

Para cada eletrodo, devemos calcular o potencial do eletrodo usando a equação de Nernst.

Se tivermos reação:

a equação de Nernst é:

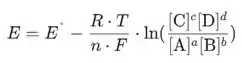
Se substituirmos valores numéricos por constantes e convertermos para logaritmo de base 10, obteremos:

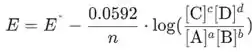
onde E° é o potencial de eletrodo padrão e n é o número de mols de elétrons para semirreação

  1. Temos a seguinte meia-célula:

    2. N i   ∣   N i 2 + ( 0.0943 )   M

    A reação é:

    N i 2 + + 2   e - → N i

    onde o potencial de redução padrão para esta reação é:

    E ° = - 0.257 V

    A equação de Nernst para esta reação é:

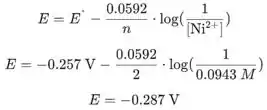
    Vemos que o potencial do eletrodo é mais positivo que o eletrodo de hidrogênio padrão (0 V), então este é catodo.

  2. Temos a seguinte meia célula:

    3. A g   ∣   A g I ,   K I   ( 0.0922 )   M

    A reação é:

    A g I + e - → A g + I -

    onde o potencial de redução padrão para esta reação é:

    E ° =   - 0.152   V

    A equação de Nernst para esta reação é:

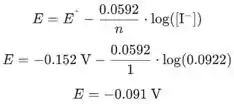
    Vemos que o potencial do eletrodo é mais negativo que o eletrodo de hidrogênio padrão ( 0 V ), então este é anodo.

    Passo 2

  3. Temos a seguinte meia célula:

    4. P t ,   O 2 ​   ( 780 )   t o r r ,   H C l   ( 1.5 ⋅ 10 - 4 )   M

    A reação:

    O 2 ​ + 4   H + + 4   e - → 2   H 2 ​ O

    onde o potencial de redução padrão para esta reação é:

    E ° = 1.229   V

    A equação de Nernst para esta reação é:

    Vemos que o potencial do eletrodo é mais positivo que o eletrodo de hidrogênio padrão ( 0 V ), então este é catodo.

  4. Temos a seguinte meia célula:

    5. A reação é:

    S n 4 + + 2 e - → S n 2 +

    onde o potencial de redução padrão para esta reação é:

    E º = 0.154   V

    A equação de Nernst para esta reação é:

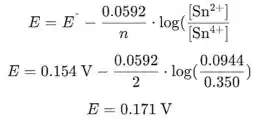
    Vemos que o potencial do eletrodo é mais positivo que o eletrodo de hidrogênio padrão ( 0 V ), então este é catodo.

    Passo 3

  5. Temos a seguinte meia célula:

A g   ∣   A g S 2 ​ O 3 ​ 2 3 - ​ ,   0.00753   M   N a 2 ​ S 2 ​ O 3 ​   ( 0.1439 )   M

A reação é:

A g S 2 O 3 2 3 - ​ + e - → A g + 2   S 2 O 3 2 -

onde o potencial de redução padrão para esta reação é:

E ° =   0.017   V

A equação de Nernst para esta reação é:

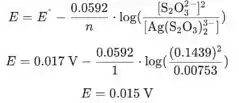
Vemos que o potencial do eletrodo é mais negativo que o eletrodo de hidrogênio padrão ( 0 V ), então este é ânodo.

Resposta

Ver o desnevolvimento

Exercícios de Livros Relacionados

Por que é necessário borbulhar hidrogênio na solução do eletrólito em um eletrodo de hidrogênio?
Apresente uma distinção clara entre: *(a) redução e agente redutor. (b) uma célula galvânica e uma célula eletrolítica. *(c) o ânodo e o cátodo em uma célula eletroquímica. (d) uma célula eletroquímic
A constante do produto de solubilidade para o P b 3 A s O 4 2é4,1 × 10 - 36 é . Calcule E 0 para a reação P b 3 A s O 4 2 s + 6 e - ⇋ 3 P b s + 2 A s O 4 2 -
Calcule E^0 para o processoC u (N H_3)_4^(2 +) + e^- ⇋ C u (N H_3)_2^+ + 2 N H_3 Sabendo queC u^+ + 2 N H_3 ⇋ C u (N H_3)_2^+ beta_2 = 7.2 xx 10^(10) C u^(2 +) + 4 N H_3 ⇋ C u (N H_3)_4^+ beta_4 = 5.6
Calcule o tempo necessário para uma corrente constante de 1,20 A para depositar 0,500 g de (a)T l ( I I I ) na forma do elemento em um cátodo. (b) T l ( I ) como T l 2 O 3 no ânodo.(c )T l ( I ) na fo