Enunciado
Química - Fundamentos de química analítica, Skoog- Ed: 8º - Capítulo 18.Questões e Problemas - Ex. 16
Calcule o potencial de um eletrodo de platina imerso em uma solução que seja:
Passo 1
Nesta tarefa, precisamos calcular o potencial de um eletrodo de platina.
A tendência de um metal oxidar é uma medida do potencial do eletrodo. Diferentes metais têm diferentes tendências de oxidação e, portanto, diferentes potenciais de eletrodo.
Em geral, um metal imerso em uma solução de seus próprios íons forma um semi-membro correspondente.
Em uma célula galvânica, a energia química é convertida espontaneamente em energia elétrica. A célula galvânica consiste em duas meias-células diferentes conectadas por um condutor e uma ponte eletrolítica. O eletrodo no qual ocorre o processo de oxidação é chamado de ânodo e é o pólo negativo da célula. O eletrodo no qual ocorre o processo redução é chamado de cátodo e é o pólo positivo da célula.
- A reação no eletrodo de platina é:
- A reação no eletrodo de platina é:
- A reação no eletrodo de platina é:
- A reação no eletrodo de platina é:
- A reação no eletrodo de platina é:
- A reação no eletrodo de platina é:
O potencial de redução padrão para esta reação é:
A equação de Nernst para esta reação é:
Observe que a platina elementar não está incluída na equação porque está em fase sólida. A dissociação de
De acordo com a equação temos que a quantidade de mols de é igual a de Então a concentração de ambos é a mesma:
A dissociação do KCl é:
De acordo com a reação, a quantidade de mols de ambos é a mesma. Sendo assim, a concentração de ambos também é a mesma.
Agora colocamos valores na equação de Nernst para obter o potencial do eletrodo:
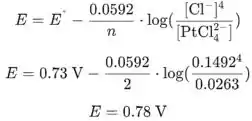
O potencial de redução padrão para esta reação é:
A equação de Nernst para esta reação é:
Segundo a equação a quantidade de mols de é igual a de . Sendo assim a concentração de ambos também é a mesma e é de 0.0750 M.
Segundo a equação a quantidade de mols de é igual a de . Sendo assim a concentração de ambos também é a mesma e é de M.
Agora colocamos valores na equação de Nernst para obter o potencial do eletrodo:
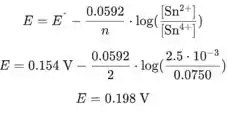
Passo 2
O potencial de redução padrão para esta reação é:
A equação de Nernst para esta reação é:
Calculamos a concentração de usando o pH da solução
Agora colocamos valores na equação de Nernst para obter o potencial do eletrodo:
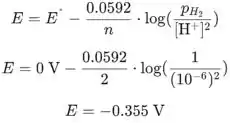
O potencial de redução padrão para esta reação é:
A equação de Nernst para esta reação é:
De acordo com a reação, a quantidade de mols de é igual a de . Então a concentração é a mesma e é de 0.0353 M.
De acordo com a equação, a quantidade de mols de
Então a concentração é de:
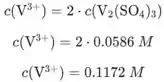
Passo 3
O potencial de redução padrão para esta reação é:
A reação de
Devemos multiplicar a segunda equação por 2 para equilibrar os elétrons:
A soma dessas duas equações é:
Agora colocamos valores na equação de Nernst para obter o potencial do eletrodo:
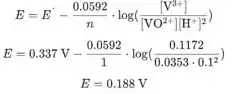
Agora devemos calcular a quantidade de íons que é consumida.
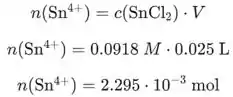
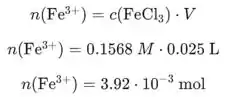
Usando a equação:
calculamos a quantidade de que se formam.
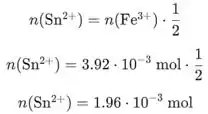
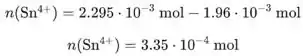
Agora colocamos valores na equação de Nernst para obter o potencial do eletrodo:
O potencial de redução padrão para esta reação é:
A equação de Nernst para esta reação é
Agora devemos calcular a quantidade de íons que é consumida.
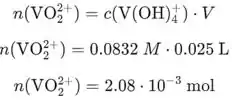
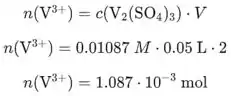
calculamos a quantidade de que se formam.
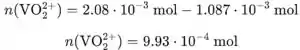
Calculamos a concentração de usando o pH da solução:
Agora colocamos valores na equação de Nernst para obter o potencial do eletrodo:
Resposta
a) E = 0.78 V b) E = 0.198 V c) E = - 0.355 V d) E = 0.188 V e) E = 0.131 V f) E = 0.879 V