Enunciado
Química - Fundamentos de química analítica, Skoog- Ed: 8º - Capítulo 3.Questões e Problemas - Ex. 10
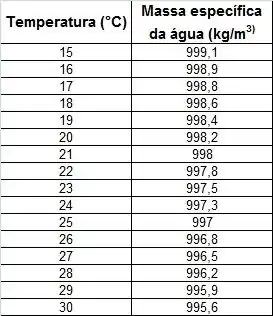
Exercício Desafiador. A Equação 2-1 permite o cálculo da correção do empuxo do ar para os dados de massa. Suponha que esteja calibrando uma pipeta de 100 mL por meio da pesagem de alíquotas de água em uma balança analítica e deseja preparar uma planilha para corrigir suas massas de água, para o empuxo, a várias temperaturas. A coluna final da sua planilha deve conter o erro porcentual na pesagem, em função da temperatura. Como ponto de partida, use a tabela de densidades da água que você obteve na Seção Exercícios na Web, neste capítulo. Alternativamente, você pode procurar os dados no CRC Handbook of Chemistry and Physics ou outra fonte de referência e digite-os na sua planilha. Use a lei dos gases ideais para calcular a densidade do ar a temperaturas de 15 °C a 30 °C, em intervalos de um grau. Considere que o ar tenha 78% de nitrogênio e 22% de oxigênio, que a densidade das massas-padrão usados para calibrar sua balança seja de 8,0 g/cm3 e a pressão atmosférica, de 1 atm.
- Seus resultados indicam que é necessário fazer correções devido ao empuxo do ar quando se calibra uma pipeta? Justifique.
(b) A temperatura é uma variável importante na correção para o empuxo durante a calibração de uma pipeta? Explique.
(c) Que outro papel sua tabela de densidade da água, em função da temperatura, desempenha na calibração de uma pipeta?
(d) Se você fez dez réplicas de determinações da massa de água dispensada por uma pipeta de 100 mL e a massa aparente média da água dispensada a 19 °C foi de 99,736 g, qual o volume corrigido da pipeta?
(e) Qual o volume da pipeta corrigido para o empuxo do ar em suas pesagens?
(f) Um fator adicional que determina o volume de líquido dispensado por uma pipeta é a expansão e a contração do vidro, à medida que a temperatura se altera. O volume do recipiente de vidro a uma dada temperatura T é dado por VT V20[1 a(T – 20 °C)], em que V20 é o volume do recipiente a 20 °C e a é coeficiente de expansão cúbico do vidro. O coeficiente de expansão cúbico varia com o tipo de vidro, mas para o vidro típico de borossilicato, a 0,000010 mL/mL/°C. Adicione uma coluna à sua planilha que corrija a expansão do vidro com a temperatura e comente sobre esse efeito em relação a outros efeitos que você tenha investigado.
(g) Qual o volume verdadeiro da pipeta de 100 mL
Passo 1
Beleza Pessoal?! Espero que sim, me chamo Yuri e hoje iremos dar início a mais uma resolução com o padrão de qualidade do responde aí, vem comigo!!!
- A equação 2-1 do livro é a seguinte:
- A situação é semelhante à alternativa anterior, pela equação geral dos gases perfeitos, notamos que a temperatura é um influenciador na densidade, e consequentemente influencia nas medições. Mas tudo depende do grau de precisão que deseja nas suas medições
- A influência da dilatação volumétrica em relação aos outros fatores é menor nesse caso, temos uma constante de dilatação extremamente menor que os outros fatores que influenciam na calibração da pipeta.
em que P1 é a massa corrigida do objeto, P2 é a massa dos padrões, dobj. é a densidade do objeto, dmassas é a densidade das massas padrão e dar é a densidade do ar deslocado por eles; dar tem um valor de 0,0012 g/cm3.
Temos que dmassas = 8,0 g/cm3, dado fornecido pelo enunciado.
Se notarmos a equação 2-1 e a equação geral dos gases, notamos que a correção é justificada, a densidade varia em relação a temperatura, sendo assim os dados terão erros caso não sejam corrigidos. Mas tudo isso depende do grau de precisão que deseja buscar para suas medições.
Passo 2
Isso influencia diretamente no empuxo, e consequentemente influencia nas medições e deve ser levado em consideração na calibração. A fórmula do empuxo é dada por , podemos notar então claramente a relação de proporcionalidade entre a densidade e o empuxo.
Passo 3
Resposta
Ver o desenvolvimento