Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Química - Atkins - Fisico-Quimica - Vol. 1- Ed: 8º - Capítulo 5.Problemas Numéricos - Ex. 10

As misturas de cicloexano e diversos alcanos de cadeias longas foram investigadas por Aminabhavi et al. (T.M. Aminabhavi, V.B. Patil, M.I. Aralaguppi, 1.0. Ortego, and K.C. Hansen, J. Chem. Eng. Data 41, 526 (1996). Entre os dados publicados figuram os das massas específicas das soluções de cicloexano e pentadecano em função da fração molar do cicloexano ( x C ) a 298,15 K.

Calcule o volume parcial molar de cada componente na solução que tem a fração molar do cicloexano igual a 0,7988.?

Passo 1

Falaaaaaaaaaaaaaaaa Tribuxo?

Bora resolver mais uma questão!?

Vamos começar escrevendo a equação para o volume molar do ciclohexano:

V C = ∂ V ∂ n C p , T , n 2  

O mesmo pode ser escrito para. Podemos avaliar V C graficamente, plotando um gráfico de V × n C , achando a inclinação; o mesmo pode ser feito para V P , trançando um gráfico de V × n P .

Para acharmos V C , vamos precisar de V em uma variedade de pontos para n C , e para isso iremos trabalhar com n p = c t e = 1   m o l , e depois faremos o mesmo com n C para achar V P .

Como temos dados da fração molar:

x C = n C n C + n P

E podemos achar n C , vamos manipular a equação acima, primeiro multiplicando tudo por n C + n P :

x C n C + n P = n C

x C n C + x C n P = n C

Isolando n C :

x C n P = n C - x C n C

x C n P = n C 1 - x C

n C = x C n P 1 - x C

Para achar V , faremos:

V = m ρ

Onde m é a massa total, então:

m = m C + m P

Podemos achar a passa por:

n = m M

m = n M

Voltando para:

Onde:

m = m C + m P

m = n C M C + n p M p

Substituindo na fórmula do volume:

V = n C M C + n P M P ρ

Passo 2

Agora só precisamos montar a tabela:

Agora plotando os gráficos de V × n C e V × n P :

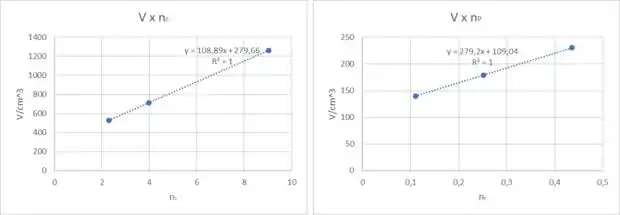
Passo 3

Teremos que V C e V P serão as inclinações, então:

V C = 108,89   c m 3   .   m o l - 1

V P = 279,2   c m 3   .   m o l - 1

Foi divertido!!!!

Bora matar mais uma!

Resposta

V C = 108,89   c m 3   .   m o l - 1

V P = 279,2   c m 3   .   m o l - 1

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

A pressão de vapor de um líquido puro A é 68,8 K P a a 293 K e a de outro líquido B, também puro, é de 82,1 K P a . Esses dois compostos formam soluções líquidas ideais e misturas gasosas também ideai
O dibrometano (DE, ρ ˙ D E = 22,9 K P a a 358 K ) e o dibromopropeno (DP, ρ ˙ D P = 17,1 K P a a 358 K ) formam uma solução praticamente ideal. Se z D E = 0,60 , qual é (a) a pressão total, ρ t o t a
O benzeno e o tolueno formam soluções praticamente ideiais. Considere uma solução equimolar de benzeno e tolueno. A 20 ° C , a pressão de vapor do benzeno puro é 9,9 K P a e a do tolueno puro é 2,9 K
O ponto de ebulição de uma solução binaria de A e B, com x A = 0,6589 , é 88 ° C . Nesta temperatura, a pressão de vapor de A puro é 127,6 K P a e a de B puro é 50,60 K P a . A solução é ideal?Qual a
O ponto de ebulição de uma solução binaria de A e B, com x A = 0 , 4217 , é 96 ° C . Nesta temperatura, a pressão de vapor de A puro é 110,1 K P a e a de B puro é 76,5 K P a . A solução é ideal?Qual a