Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Química - Atkins - Fisico-Quimica - Vol. 1- Ed: 8º - Capítulo 5.Problemas Numéricos - Ex. 9

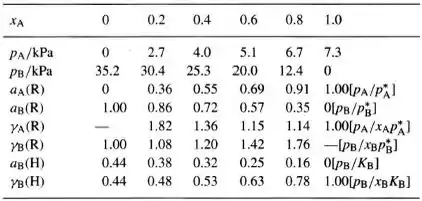
9 – A partir dos dados que são vistos a seguir, faça o gráfico da pressão de vapor para uma mistura de benzeno (B) e ácido acético (A) a trace a curva da pressão de vapor/composição para a mistura a 50°C. Confirme que as leis de Raoult e de Henry são verificadas nas regiões apropriadas. Obtenha as atividades e os coeficientes de atividade dos componentes com base na lei de Raoult e, então, tomando B como soluto, determine a sua atividade e o seu coeficiente de atividade com base n alei de Henry. Finalmente, estime a energia de Gibbs de excesso para a mistura em toda a faixa de composições mostrada pelos dados.

Passo 1

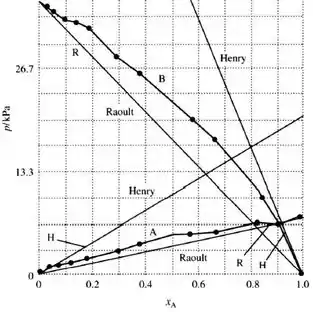
Com os dados da tabela dada no enunciado, tem-se o seguinte gráfico para pressão de vapor em função da composição x:

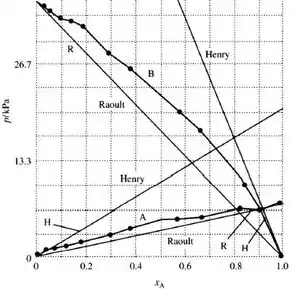
Pelo gráfico acima, as regiões onde a curva da pressão de vapor se aproxima das linhas retas são denotadas por R para Raoult e H para Henry.

Passo 2

Os coeficientes de atividade da lei de Raoult são dados por:

γ A = p A x A p A *

γ B = p B x B p B *

O coeficiente de atividade para o benzeno (B) na lei de Henry é dado por:

γ B = p B x B K

Onde, K é a constante de Henry que pode ser determinado por extrapolação usando o gráfico obtido para a pressão de vapor em função da composição.

Passo 3

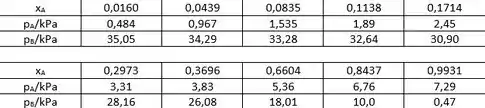
Os valores para as pressões p*, para os dois componentes A e B são:

p A * = 7,3   k P a

p B * = 35,2   k P a

O coeficiente de Henry para o benzeno é:

K B = 80,0   k P a

Assim, podemos calcular os coeficientes de atividade para cada composto usando expressões de Henry e Raoult.

Pegando as expressões anteriores mostradas a aplicando os valores obtemos os seguintes valores:

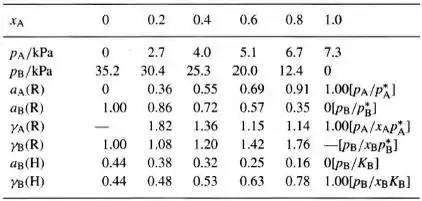
Passo 4

A energia de Gibbs de excesso é dada pela seguinte expressão, encontrada na Seção 5.4:

G E = ∆ m i x G r e a l - ∆ m i x G i d e a l

Onde,

∆ m i x G r e a l = n R T x A ln ⁡ a A + x B ln ⁡ a B

∆ m i x G i d e a l = n R T x A ln ⁡ x A + x B ln ⁡ x B

Para o qual ‘a’ é a atividade, dada por

a = γ x

Assim, vamos ter que:

G E = n R T x A ln ⁡ a A + x B ln ⁡ a B - n R T x A ln ⁡ x A + x B ln ⁡ x B

G E = n R T x A ln ⁡ γ A + x B ln ⁡ γ B

Passo 5

Considerando o nº de mols sendo uma unidade, assim

n = 1,0   m o l

Sendo R a constante dos gases ideais:

R = 8,314   J   m o l - 1 K - 1

Assim,

R T = 8,314   J   m o l - 1 K - 1 323   K = 2,69   k J   m o l - 1

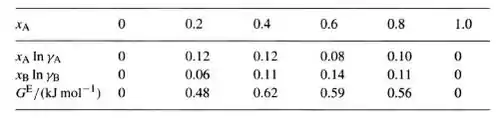
Com os valores acima e com a equação para a energia de Gibbs de excesso mostrada anteriormente, podemos calcular as energias de Gibbs para a faixa de composição e obtemos os seguintes valores:

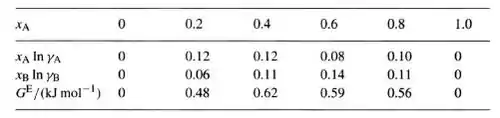
Resposta

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

A hemoglobina, o pigmento vermelho do sangue responsável pelo transporte do oxigênio, liga-se a cerca de 1,34c m 3 de oxigênio por grama. O sangue normal tem uma concentração de hemoglobina de 150g.d
A medida das composições das fases líquidas e vapor em equilíbrio, de uma solução binária a 30 ℃ ℃ a 1 atm, mostrou que x A = 0,220 quando y A = 0,314 . Calcule as atividades e os coeficientes de ativ
A medida das composições das fases líquida e vapo, em equilíbrio, de soluções de acetona (A) e metanol (M) mostrou que, a 57,2 ℃ ℃, sob pressão de 1 atm, tem-se x A = 0,4 e quando y A = 0,516 . Calcul
Uma solução diluída de bromo em tetracloreto de carbono comporta-se como uma solução diluída ideal. A pressão de valor do C C l 4 puro é 33,85 T o r r , a 298K. A constante da lei de Henry quando a co
O equilíbrio líquido-vapor do triclorometano e 1,2-epoxibutano foi estudado a várias temperaturas por Francesconi et al. (R. Francesconi, B. Lunelli e F. Comelli, J. Chem. Eng. Data 41, 310 (1996)). E