Enunciado
Química - Atkins - Fisico-Quimica - Vol. 1- Ed: 8º - Capítulo 12.Problemas Numéricos - Ex. 11
R. Eujen, B. Hoge e D.J Brauer [Inorg. Chem. 36, 1464 (1997)] prepararam e caracterizaram diversos ânions complexos, planos quadrados, do . No ânion complexo os grupos são colineares. (a) Admitindo a rotação livre dos grupos (isto é, não levando em conta os ângulos e ), identifique o grupo de simetria desse ânion complexo. (b) Imagine agora que os grupos não podem girar livremente (por estar, por exemplo, o íon fixo num sólido). A estrutura (26) mostra um plano que corta simetricamente o eixo e é perpendicular a ele. Dê o grupo de simetria do íon complexo na hipótese de cada ter uma ligação nesse plano (de modo que os grupos não apontam, preferencialmente, para qualquer dos dois grupos ) e os grupos estarem (i) deslocados angularmente (escalonados) e (ii) eclipsados.
Passo 1
Calmaaa, tira essa carinha de desespero e vamos lá
a) O primeiro passo aqui é desenhar a nossa molécula. Como os grupos rodam livremente, podemos desenhar nossa molécula assim:
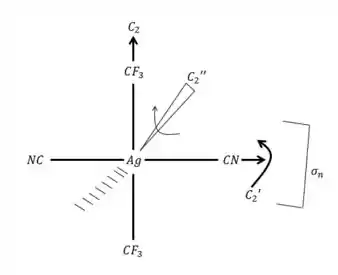
Temos que e são perpendiculares a , dessa forma, já sabemos que temos um grupo do tipo
Também temos que é perpendicular ao eixo principal (que é o de )
Dessa forma, o grupo formado é , fechou?
Passo 2
b) Agora vamos considerar os grupos fixos e (i) escalonados e (ii) eclipsados
Para a situação (i), temos apenas um eixo que passa por
Nesse caso, também há o plano perpendicular ao eixo , e que também corta os dois grupos
Nossa molécula nesse caso fica assim:
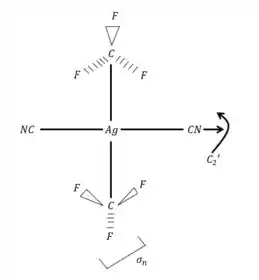
O eixo principal agora é , que é perpendicular a
Dessa forma, seguindo as regras de grupos moleculares, notamos que esse é o grupo
Passo 3
Para o caso (ii), temos um eixo passando por e o plano que também corta os dois grupos
A molécula fica assim:
Dessa forma, temos a simetria
Ufa, acabouuuu
Resposta
a)
b) (i) (ii)