É possível ver, com a ajuda de um poderoso microscópio, que um fragmento de um DNA de dupla fita é flexível, com uma ampla faixa de valores para a distância entre as extremidades da cadeia. Essa flexibilidade é importante, porque permite que o DNA adote conformações muito compactas quando empacotado num cromossoma (veja o Capitulo 18). É conveniente visualizar esse longo fragmento de DNA como uma cadeia com articulações livres, uma cadeia formada por N pequenas unidades rígidas, cada uma de comprimento I, que podem fazer qualquer ângulo uma em relação outra. O comprimento l, denominado comprimento de persistência, é de aproximadamente 45 nm, correspondendo a cerca de 130 pares de base. Neste problema, você vai determinar o trabalho necessário para alongar uma molécula de DNA. (a) Suponha que a resistência de uma molécula de DNA ao alongamento a partir de sua posição de equilíbrio, na conformação mais compacta, seja descrita por uma força restauradora F=-kf x, onde x é a diferença entre as extremidades da cadeia em relação à correspondente distância na posição de equilíbrio, e kf é a constante de força. Sistemas que mostram esse comportamento obedecem a lei de Hooke. (i) Quais são as limitações desse modelo da molécula do DNA? (ii) Usando esse modelo, obtenha a expressão do trabalho necessário para alongar a molécula de DNA de um valor x. Faça um gráfico de seus resultados. (b) Um modelo melhor para a molécula de DNA é a cadeia com articulações livres unidimensional na qual uma unidade (leia articulações livres unidimensional, na qual uma unidade rígida de comprimento I só pode fazer um ângulo de 0° ou de 180° com a unidade adjacente. Neste caso, a força restauradora de urna cadeia alongada de x=nl é dada por:
Nesta equação, k = 1,381 é a constante de Boltznmnn (não é uma constante de força). (i) Quais são as limitações desse modelo? (ii) Qual é a magnitude da força que deve ser aplicada para alongar uma molécula de DNA com N = 200 de 900 nm? (iii) Faça um gráfico da força restauradora contra v, observando que essa grandeza pode ser positiva ou negativa. Como se compara a variação da força restauradora com a distância entre as extremidades obtida por esse modelo com a prevista pela lei de Hooke? (iv) Lembrando que a diferença na distância entre as extremidades em relação a essa grandeza na posição de equilíbrio é x = nl e que Idn = Nldv, obtenha uma expressão para o trabalho necessário pata alongar uma molécula de DNA. (v) Calcule o trabalho necessário para alongar urna molécula de DNA de v = 0 a v = 1,0. Sugestão. Você deve integrar a expressão para w. A tarefa pode ser realizada utilizando-se um software matemático. (c) Mostre que, para pequenos alongamentos da cadeia, quando v
Sugestão. Veja o Apêndice 2 para uma revisão de expansão em série de uma função. (d) A variação da força restauradora com o alongamento da cadeia obtida no item (c) é diferente da prevista pela lei de Hooke? Explique sua resposta.
Passo 1
E aí pessoal, tudo bom? Esse enunciado é grande mas vamos com calma parte por parte.
(a)(i) Uma das principais limitações da lei de Hooke é que ela se aplica a deslocamentos de um único equilíbrio valor da distância ponta a ponta. De fato, se uma molécula de DNA ou qualquer outra cadeia macromolecular que é suscetível a fortes interações intramoleculares de não ligação é suficientemente perturbado de uma configuração de equilíbrio, é provável que se estabeleça em uma configuração de equilíbrio diferente, um chamado "mínimo local" em energia potencial. A lei de Hooke é uma boa aproximação para sistemas que têm uma única configuração de equilíbrio correspondente a um único mínimo em energia potencial.
Passo 2
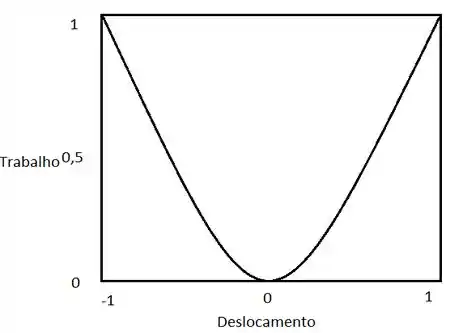
(a)(ii) A expressão do trabalho para o que é pedido é dada por:
Agora faremos um gráfico que deve ter semelhança com o gráfico a seguir:
Passo 3
(b)(i) Uma limitação evidente é que o modelo trata apenas de deslocamentos ao longo dos deslocamentos que interrompem a corrente.
Passo 4
(b)(ii)A magnitude da força que deve ser aplicada para alongar uma molécula de DNA com N = 200 de 900 nm será calculada por:
Passo 5
(b)(iii) Para pequenos deslocamentos, as parcelas quase coincidem. No entanto, para grandes deslocamentos, a magnitude da força no modelo unidimensional cresce muito mais rápido.
Passo 6
(b)(iv) Agora vamos obter uma expressão para o trabalho necessário para alongar uma molécula de DNA:
Passo 7
(b)(v) Agora vamos calcular o trabalho necessário para alongar uma molécula de DNA de v = 0 a v = 1,0. Para isso integramos a expressão do item (b)(iv) e fazemos:
Passo 8
(c) Agora vamos mostrar que para pequenos alongamentos da cadeia, quando v
Para isso, faremos:
Passo 9
(d) A derivação na parte (c) confirma: que ele é unidimensional e o modelo de cadeia e a lei de Hooke têm o mesmo comportamento para pequenos deslocamentos.
Resposta
Ei, a resposta está no passo a passo :)