Enunciado
Química - Fundamentos de química analítica, Skoog- Ed: 8º - Capítulo 8.Questões e Problemas - Ex. 20a
O potássio pode ser determinado por espectrometria de emissão em chama (fotometria de chama) usando um padrão interno de lítio. Os seguintes dados foram obtidos para soluções padrão de e uma solução desconhecida contendo uma quantidade constante de como padrão interno. Todas as intensidades foram corrigidas pela subtração da intensidade de emissão do branco.
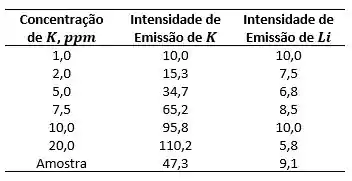
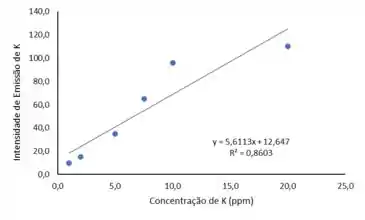
- Construa um gráfico da intensidade de emissão de a concentração de e determine a linearidade a partir da regressão estatística.
Passo 1
Oi galerinha, estou feliz em te ver por aqui, vem comigo! Para a construção do gráfico, iremos utilizar o programa Excel, mas fiquem calmos que irei te ajudar. Primeiramente iremos colocar nossos dados no programa, onde iremos considerar:
Concentração de K;
Intensidade de Emissão de K.
Então, iremos inserir os dados e selecioná-los:
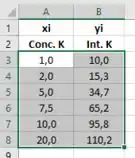
Então clicamos na aba “Inserir” e na opção “Gráficos”, escolhemos “Dispersão”:
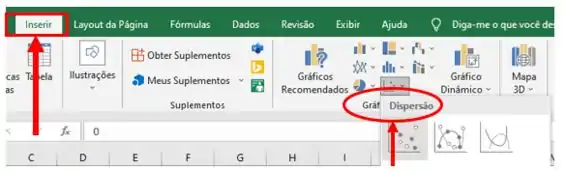
Nosso gráfico será criado e precisamos colocar a linha de tendência linear. Iremos clicar no símbolo () à direita do gráfico, selecionar a opção “Linha de Tendência” e escolher a opção “Linear”, como está descrito abaixo:
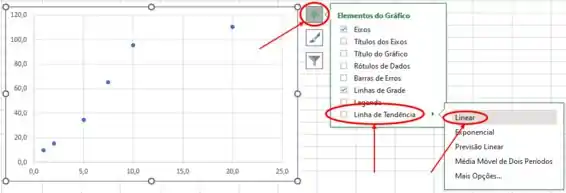
Passo 2
E assim iremos obter o gráfico a seguir:
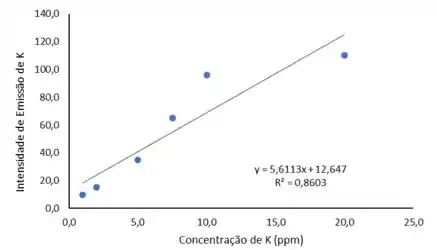
Com isso temos o valor do coeficiente de correlação:
E nossa equação da reta:
Onde:
Inclinação da reta: ;
Intercepto: .
Pelo gráfico conseguimos perceber que o ajuste linear não está bom e além disso temos um coeficiente de correlação baixo ().
Passo 3
Além do coeficiente de correlação, podemos determinar o valor , para avaliarmos melhor nossa regressão, para isso utilizaremos:
Para chegarmos neste valor, vamos fazer alguns cálculos primeiramente, como não conhecemos a concentração da última amostra, iremos considerar :
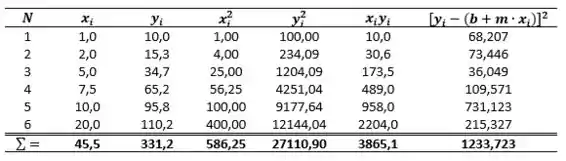
Onde, temos a soma dos quadrados:
A soma total dos quadrados tem 5 graus de liberdade associados a ela. A soma dos quadrados devido aos resíduos possui 4 graus de liberdade. Além disso, tem apenas 1 grau de liberdade. Logo:
Sendo assim:
Com o valor , é outro indicativo de que nossa regressão não é significativa, ou seja, não é linear.
Prontinho pessoal, espero que tenha conseguido te ajudar, até mais.
Resposta
O ajuste linear não está bom ( e ).
