Problema Desafiador. Como vimos no Problema 19-16, como um experimento preliminar em seu trabalho para medir a constante de dissociação do ácido acético, Herned e Ehlers mediram E0 para a célula mostrada sem junção líquida. Para completar o estudo e determinar a constante de dissociação, esses pesquisadores também mediram o potencial da seguinte célula.

c) Neste exercício, devemos responder o que acontece com o lado direito da equação deduzida na parte b) quando a força iônica se aproxima de 0. Vamos expressar a equação novamente:

O coeficiente de atividade de um íon (o de uma molécula é assumido como 1) se aproxima de 1 quando a força iônica se aproxima de 0. Portanto, neste caso, ocorre o seguinte:

Como qualquer logaritmo com um argumento de 1 produz 0, este adendo é retirado e a equação é simplificada para o seguinte:

d) Nesta parte, devemos mostrar que o lado direito da equação mostrada como resultado da parte c), pode ser indicado da seguinte forma:

Alternando E e E° significa a mudança do sinal do expoente

Isso significa que, na verdade, K é dado como mencionado no exercício, não K'

e) Nesta parte, é dado que de acordo com Harned e Ehlers, a força iônica da solução é dada da seguinte forma:

onde é a molalidade de NaOAc, é o de NaCl e é a dos prótons. Devemos provar que esta expressão está correta.

A força iônica, geralmente, é dada de acordo com a seguinte fórmula:

onde c representa a concentração dos respectivos íons e z representa a carga deles. No caso de solução suficientemente diluída, isso também pode ser expresso pelas molalidades dos íons:

Vamos expressar a equação incluindo as identidades químicas dos íons. Observe que H+forma na dissolução do ácido acético (nem todos se dissocia). Como todos os íons carregam uma única carga e um íon se dissocia de uma molécula, a molalidade dos íons é igual à molalidade das moléculas das quais eles derivam. No caso da última molécula, vamos indicar ambos os íons como a molalidade do cátion.

Vamos simplificar a equação. A molalidade dos dois primeiros adendos são de fato , respectivamente.:

Esta equação é de fato a mesma que mencionamos no início desta parte, então sua identidade foi comprovada.

f) Neste exercício, devemos determinar se a notação na concentração molar indicada na tabela é molar analítica ou concentrações de equilíbrio molar. Neste, e no exercício anterior, a molalidade foi determinada como o produto da concentração de equilíbrio e o coeficiente de atividade. Portanto, pela convenção dada pelo livro, a unidade dada é a concentração de equilíbrio.

g) Nestas partes, devemos determinar o valor a 25°C. No entanto, o E∘ valor do processo não é dado. Portanto, vamos calcular com os dados padrão calculados no Problema 506-16. Primeiramente, vamos indicar as molalidades de equilíbrio. A molalidade do próton é dada como segue (devido ao baixo de ácido acético):

Ao final, deve-se fornecer a força iônica, conforme determinado na parte e):

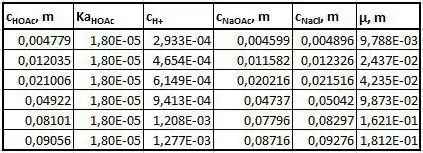
Conhecendo a força iônica, vamos calcular o K' valores de acordo com a fórmula determinada anteriormente.

Observe que esta fórmula não fornecerá nenhuma linearidade, portanto, isso deve ser equivocado, da mesma forma que o erro do exercício da parte d). Portanto, a fórmula correta deve ser assim:

Vamos novamente escrever uma forma diferente desta equação:

Isso significa que a interceptação (eixo y: K', eixo x: μ) deve fornecer o valor K, que é o valor do ácido acético, no nosso caso. Vamos resumir os valores dados em uma tabela.

Como pudemos ver, o valor provisório do de ácido acético tem pouco efeito no valor final, pois tem impacto apenas na concentração de prótons, que é uma pequena fração da força iônica. Isso significa que, na próxima parte (embora isso não seja totalmente preciso, pois o valor fornecido é definido para 25°C), vamos usar esse valor em outras temperaturas também, pois não faz grandes discrepância para o calculado. Como podemos ver, os valores são de fato bastante próximos uns dos outros e, portanto, a linearidade é sensível a qualquer tipo de imprecisão durante a medição. Como resultado, o valor gerado é ligeiramente diferente do aceito valor. h) Nesta parte, devemos traçar o K' versus a força iônica novamente e determine , agora em todas as outras temperaturas dadas. Além disso, devemos observar como o varia com a temperatura, e em que temperatura podemos observar um máximo. Vamos novamente resumir os dados na tabela e mostrar os gráficos.

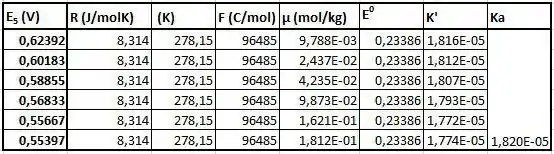
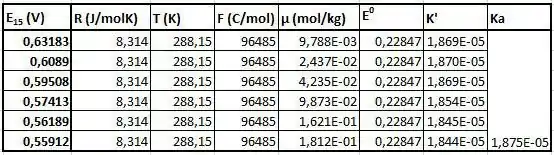
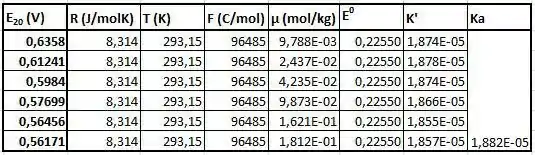
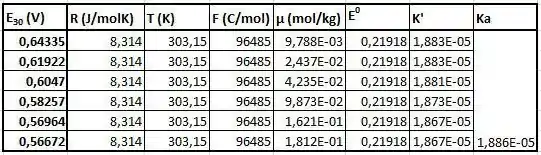
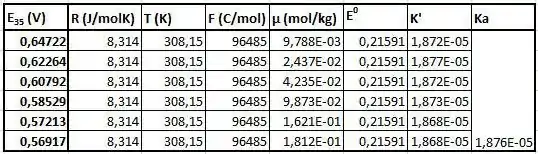
Ao final, vamos observar a dependência da temperatura do .