94. (a) Use o mecanismo abaixo e derive a Eq.19ª, que Michaelis e Meten propuseram como representação da velocidade de formação de produtos em uma reação catalisada enzimaticamente.(b) Mostre que a velocidade é independente da concentração do substrato em altas concentrações do substrato.
Passo 1
Letra (a)
Lembre-se da seguinte equação:
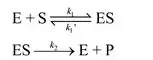
Aqui, E é a enzima livre, S é o substrato, ES é o complexo enzima-substrato, P é o produto e k é a taxa constante para as respectivas etapas.
Passo 2
Lembre-se de que a concentração no estado estacionário da enzima livre será a seguinte:
Portanto, a qualquer momeno, a concentração desse intermediário permanece constante:
Nós sabemos isso,
Da equação (1) e (2), podemos escrever:
Passo 3
A taxa da reação é dada abaixo:
Aqui,
é a constante de Michaelis.
Portanto, a taxa da reação é dada pela equação:
Passo 4
Letra (b)
Quando a concentração do substrado é muito alta, a equação da taxa pode ser escrita da seguinte maneita:
No caso acima [S]>>KM, então
Portanto, a taxa de reação é independente da concentração do substrato em altas concentrações de substrato.
Resposta
- Demonstracao
- Demonstracao