Sensibilidade
Produzido por Alexandre NunesTeoria
Introdução
Você já deve ter percebido que os sistemas com realimentação (feedback) são os mais comumente usados e por isso eles são nosso foco aqui na disciplina de Sistemas de Controle.
Esse tipo de sistema, além de responder rapidamente à maioria dos distúrbios dos processos na indústria, também são bem eficientes e precisos na maioria dos casos.
Uma outra característica que torna os sistemas com realimentação tão eficazes e robustos é que a realimentação diminui significativamente a sensibilidade do sistema.
Em alguns casos, os parâmetros dos processos, ou até mesmo dos instrumentos do sistema de controle, podem variar por conta de variações ambientais, como a temperatura do local por exemplo. Visto isso, é sempre bom escolher sistemas de controle que variem pouco com variações externas. Essa característica é chamada sensibilidade.
Sensibilidade é o quanto a resposta do sistema varia em relação à uma variação em uma função de transferência do sistema ou em um parâmetro do processo.
Parece que eu falei grego né? Vamos entender isso melhor então.

Sensibilidade e realimentação
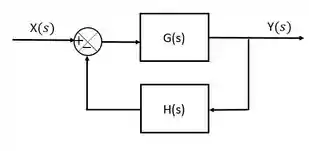
Considere o sistema sem realimentação abaixo:
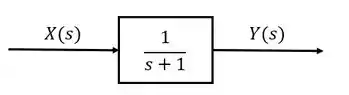
A função de transferência desse sistema é:
Vamos calcular a resposta no estado estacionário desse sistema para uma entrada degrau:
Agora, vamos alterar o polo em e ver como a resposta do sistema será alterada:
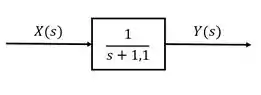
Calculando a resposta em estado estacionário para uma entrada degrau:
Sendo assim, a variação percentual da resposta é:
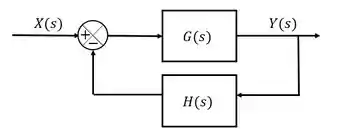
Agora vamos fazer o mesmo para um sistema realimentado:
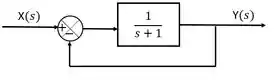
A função de transferência será:
No estado estacionário para uma entrada degrau:
Agora vamos fazer aquela mesma alteração de no polo da função de transferência:
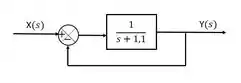
A nova função de transferência será:
No estado estacionário com entrada degrau:
Portanto a variação porcentual foi de:
Sendo assim, quando adicionamos uma realimentação em nosso sistema a variação porcentual da resposta para um acréscimo de no polo da função de transferência caiu quase pela metade, ou seja, a sensibilidade do sistema diminui drasticamente, deixando o sistema mais estável e mais robusto.
Generalizando
De modo geral, sensibilidade pode ser definido como a razão entre a variação percentual da função de transferência do sistema pela variação percentual da função de transferência central do sistema.
Vamos achar então a sensibilidade para o processo abaixo:
A função de transferência do sistema, , será:
Traduzindo o que eu disse ali em cima, nesse exemplo é a função de transferência do sistema, e é a variação percentual do sistema. é a função de transferência central do sistema, e é a variação percentual dessa função de transferência central.
A sensibilidade do sistema então será:
é a sensibilidade do sistema em relação a função de transferência .
Aplicando o limite para pequenas variações:
Como:
Eu posso derivar em :
Sendo assim:
Nesse caso, calculamos a sensibilidade do sistema com relação ao processo central da planta, entretanto, podemos calcular em relação à outras coisas como ao sensor transmissor, , ou até parâmetros da planta como ganho, ou constante de tempo. A lógica utilizada será a mesma. Por exemplo, para o sensor/transmissor:
E para um parâmetro qualquer:
Generalizando
Exercícios Resolvidos
Exercício Resolvido #1
Richard C. Dorf, Sistemas de Controle Modernos, 8ª ed., LTC, Rio de Janeiro, 2001, E4.1 – Adaptado - Pág 166.
Um sistema de malha fechada é usado para rastrear o sol e de modo a obter o máximo de energia a partir de um painel fotovoltaico. O sistema de rastreamento pode ser representado pela figura abaixo com:
Com segundo, nominalmente. Determine a sensibilidade desse sistema para uma variação em .
Passo 1
Para calcular a sensibilidade do sistema em relação a , primeiramente precisaremos calcular a função de transferência do sistema. Vamos chamar essa função de e ela pode ser encontrada através de álgebra de diagrama de blocos conforme abaixo:
Multipicando por em cima e embaixo teremos:
Passo 2
Para encontrar a sensibilidade do sistema em relação a usaremos a fórmula para a sensibilidade que está aqui ó:
Precisamos, então, calcular essa derivada. Podemos fazer usando a expressão que encontramos acima e a regrinha do quociente que aprendemos em cálculo I há 84 anos atrás:
Passo 3
Substituindo a derivada e a expressão de na fórmula da sensibilidade:
Fazendo as simplificações, teremos:
Como :
Resposta
Exercício Resolvido #2
Norman N. Nise, Engenharia de sistemas de controle, 6ª ed., Rio de Janeiro, 2012, Exemplo 7.10. Adaptado
Dado o sistema da figura abaixo, calcule a sensibilidade da função de transferência em malha fechada a variaçãos no parâmetro . Como você poderia reduzir a sensibilidade?
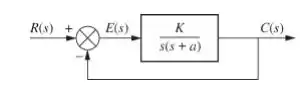
Passo 1
Primeiramente vamos encontrar a nossa função de transferência. Por álgebra de diagrama de blocos teremos:
Sendo que é a função de transferência do processo, ou seja:
Passo 2
Para encontrar a sensibilidade da função de transferência em malha fechada em relação ao parâmetro , , devemos seguir a seguinte fórmula:
Ou seja, precisamos calcular a derivade de , em relação a . Como:
Passo 3
Substituindo na fórmula da sensibilidade:
Apesar da sensibilidade em relação ao parâmetro ser uma função de , dá pra ver que para qualquer valor de , um aumento no ganho vai diminuir a sensibilidade.
Resposta
É possível diminuir a sensisbilidade aumenta o ganho .
Exercício Resolvido #3
Norman N. Nise, Engenharia de sistemas de controle, 6ª ed., Rio de Janeiro, 2012, Exemplo 7.11. Adaptado
Determine a sensibilidade do erro em regime permanente para uma entrada rampa do sistema abaixo em relação a e .
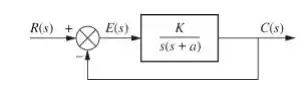
Passo 1
Antes de mais nada, precisamos definir a nossa fórmula do erro em regime permanente.
O erro pode ser calculado como:
Sendo assim, o erro em regime permanente pode ser calulado utilizando-se o teorema do valor final nessa fórmula:
Sendo que é a entrada e a função de transferência do processo.
Para o nosso exercício, temos uma entrada rampa e a função de transferência é dada na figura:
Portanto:
Passo 2
Sendo assim, a sensibilidade do erro em relação ao parâmetro será:
Como:
Teremos:
Passo 3
E a sensibilidade em ralação ao ganho será:
Como:
Esses resultados indicam que não é possível aumentar ou diminuir a sensibilidade do erro em regime permanente em relação a esses parâmetros. O sinal negativo na sensibilidade do ganho acontece porque um aumento em causa uma diminuição de , e vice-versa.
Resposta
Exercício Resolvido #4
Norman N. Nise, Engenharia de sistemas de controle, 6ª ed., Rio de Janeiro, 2012, Exemplo 7.12. Adaptado
Determine a sensibilidade do erro em regime permanente a variações em e em para o sistema mostrado abaixo com uma entrada degrau.
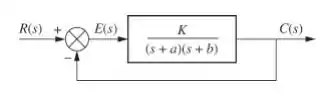
Passo 1
Primeiramente, vamos determinar o erro em regime permanente para esse sistema e entrada degrau:
Sendo assim, o erro em regime permanente pode ser calulado utilizando-se o teorema do valor final nessa fórmula:
Sendo que é a entrada, que nesse caso é um degrau e a função de transferência do processo que foi dada na figura aí em cima.
Portanto:
Passo 2
Sendo assim, a sensibilidade do erro em relação ao parâmetro será:
Usando a regra do quociente, podemos calcular:
Portanto:
Passo 3
Vamos fazer o mesmo agora para :
Usando a regra do produto novamente para calcular a derivada:
Resposta
Exercício Resolvido #5
Norman N. Nise, Engenharia de sistemas de controle, 6ª ed., Rio de Janeiro, 2012, Exercício 7.6
Determine a sensibilidade do erro em regime permanente a variações de para o sistema mostrado abaixo com uma entrada degrau.
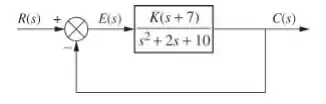
Passo 1
Bora lá. Primeiro de tudo, devemos determinar a expressão do erro em regime permanente. A fórmula do erro que conhecemos é essa:
Sendo assim, o erro em regime permanente pode ser calulado utilizando-se o teorema do valor final nessa fórmula:
é a entrada, que nesse caso é um degrau e a função de transferência do processo que foi dada na figura aí em cima.
Jogando tudo na expressão de :
Passo 2
Para encontrar a sensibilidade do erro em regime permanente em relação a , usaremos a seguinte fórmula:
A derivada, nós podemos calcular utilizando a regra do quociente:
Passo 3
Substituindo a derivada e a expressão de na fórmula da sensibilidade:
Fazendo as simplificações, teremos:
Resposta
Exercício Resolvido #6
Richard C. Dorf, Sistemas de Controle Modernos, 8ª ed., LTC, Rio de Janeiro, 2001, E4.2 – Adaptado - Pág 166.
Um sistema digital de áudio é projetado para minimizar o efeito de perturbações e de ruído, como mostra a figura abaixo.
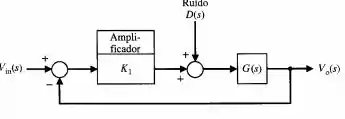
Como aproximação pode-se representar . Calcule a sensibilidade do sistema com relação a
Passo 1
Primeiramente, vamos usar álgebra de diagrama de blocos para calcular a função de transferência do sistema em malha fechada.
Como teremos:
Passo 2
Vamos usar a fórmula da sensibilidade para conseguir determinar a sensibilidade do sistema em relação a
Primeiramente, vamos calcular essa derivada enjoada aí. Como:
Podemos usar a regra do quociente e encontrar
Passo 3
Substituindo tudo na expressão da sensibilidade teremos:
Fazendo as simplificações, teremos:
Resposta
Exercício Resolvido #7
Elaboração própria
Dada a função de transferência abaixo:
Calcule .
Passo 1
Para calcular , ou seja, a sensibilidade de em ralação a , usaremos a seguinte fórmula:
Primeiramente, vamos calcular a derivada :
Passo 2
Substituindo tudo na expressão da sensibilidade teremos:
Rearranjando:
Cortando tudo que da pra cortar, ficaremos apenas com:
Resposta
Exercício Resolvido #8
Elaboração própria
Um sistema de controle é representado pelo diagrama de blocos abaixo:
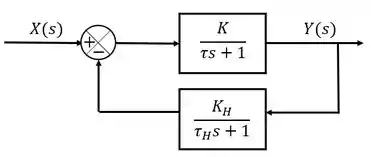
Encontre a sensisbilidade desse sistema com relação à constante de tempo do transmissor, .
Passo 1
Vamos começar determinando a função de transferência em malha fechada do sistema.
Usando as regrinhas de álgebra de diagrama de blocos teremos:
Rerranjando essa função de transferência teremos:
Passo 2
Para calcular a sensibilidade, vamos aplicar a fórmula abaixo:
Vamos começar, calculando a derivada . Como:
Podemos usar a regra do quociente e encontrar :
Passo 3
Substituindo tudo na expressão da sensibilidade teremos:
Meu deus, ficou enorme! Mas calma que dá pra simplificar um pouco: