Compensadores de atraso de fase
Produzido por Alexandre NunesTeoria
Introdução
No tópico anterior nós vimos um pouco sobre compensadores de avanço de fase. Os compensadores de avanço de fase são ótimos quando queremos melhorar as características da nossa resposta, como o tempo de sedimentação e o percentual de overshoot.
Em outros casos, porém, pode ser que aconteça de um sistema apresentar resposta com características excelentes, mas com um erro em estado estacionário muito alto.
Uma forma de reduzir o erro em estado estacionário é aumentando o ganho do sistema, mas o aumento do ganho também causa instabilidade e compromete fortemente a resposta transitória. Em muitos casos, será impossível atingir o erro em regime estacionário desejado sem tornar o sistema instável apenas aumentando o ganho.
Sendo assim, a grande questão é: como reduzir o erro em regime estacionário para um valor aceitável sem alterar ou comprometer a estabilidade do sistema?

A resposta para essa pergunta é: compensadores de atraso de fase.
Esses compensadores, quando bem projetados, são capazes de reduzir significativamente o erro em regime permanente sem alterar o ganho total da malha. Incrível né?
O compensador de atraso de fase
O compensador de atraso de fase, assim como o compensador de avanço de fase, também tem função de transferência geral do tipo:
A diferença é que nos compensadores de atraso de fase, o polo do compensador é mais próximo da origem que o zero. Sendo assim:
Além disso, como o objetivo do compensador de atraso é diminuir o erro em regime permanente sem alterar as características da resposta transitória, a introdução do compensador não pode causar grandes alterações nos polos dominantes em malha fechada sem o compensador. Para que isso ocorra é necessário que o polo e o zero estejam muito próximos um do outro, porque quando isso acontece, a contribuição angular dos dois se anula e o diagrama de lugar das raízes permanece inalterado.
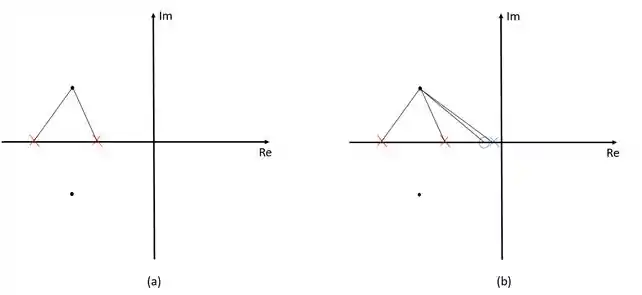
A figura acima mostra o diagrama polar para um sistema com dois polos. A figura (a) mostra o sistema sem compensação. Cada um dos polos contribui com um certo ângulo de forma que a soma dos dois seja um múltiplo ímpar de . Quando adicionamos um compensador de atraso de fase, figura (b), não queremos modificar o ponto do polo dominante, dessa forma a contribuição angular total do compensador deve ser o mais próximo de possível. Para isso, colocamos o zero muito próximo do polo, assim a contribuição angular do polo do compensador se cancela com a do zero e o polo dominante permanece inalterado.
Um outro efeito de colocar o zero e o polo muito próximos é que a distância deles para o polo dominante em malha fechada será praticamente igual, dessa forma o ganho total do sistema também não será alterado e o ganho do compensador será muito próximo de .
Além disso, para que o compensador possa de fato causar impacto sobre o erro em estado estacionário, será sempre interessante alocar o zero e o polo em valores muito pequenos e muito próximos da origem. Dessa forma, o efeito sobre o erro é sentido mais fortemente.
Dessa forma, vamos resumir as principais características do compensador de atraso de fase:
- O polo deve estar mais próximo da origem que o zero;
- O polo e o zero devem estar posicionados muito próximos um do outro;
- O polo e o zero devem ter um valor absoluto muito baixo;
- O ganho do compensador será muito próximo de .
Erro em regime permanente
Vamos fazer uma rápida revisão sobre erro em regime permanente. Nós vimos no tópico sobre erros que a fórmula para o erro em regime permanente para funções do tipo 0 será o seguinte:
Se adicionarmos um compensador:
Em alguns casos, esse limite que aparece no denominador é definido como (ou ).
Nos exercícios de projeto de compensador de atraso de fase, o erro em regime permanente sempre virá como uma especificação do projeto. Às vezes essa especificação vem na forma do próprio erro, e às vezes vem na forma de .
Imagine então que o exercício exija que o erro em regime permanente seja no máximo . Dessa forma o nosso deverá ser , pois:
Para projetar um compensador de atraso de fase, precisamos definir uma relação entre o zero e o polo do compensador, e para isso, usaremos o .
Como:
E assumindo :
Sendo assim, através do , conseguimos determinar quantas vezes o zero do compensador deve ser maior que o polo para conseguir o efeito no erro desejado.
É por isso que colocamos o polo e o zero com um valor baixo, porque imagine um caso onde a gente precisa que o zero seja dez vezes maior que o polo, se o polo fosse um valor grande, o zero ficaria extremamente afastado e já vimos que isso não é interessante. Quando colocamos o polo com um valor baixo, conseguimos colocar um zero que seja bem maior que ele (em termos relativos) sem que um esteja muito afastado um do outro.
Projeto de um compensador de atraso de fase
Vou passar agora a receita do bolo para projetar um compensador de atraso de fase:

- Esboçar o lugar das raízes para um sistema sem compensação;
- Determinar os polos dominantes para esse sistema;
- Com a especificação do erro requerido, ou do , determinar a relação entre o zero e o polo, isto é, quantas vezes o zero deve ser maior que o polo para que a especificação da faixa de erro seja atendida.
- Após determinar essa relação, deve-se arbitrar um valor para o polo. É interessante que o valor arbitrado seja baixo, entretanto, se for muito baixo o sistema pode ficar muito lento, geralmente não se recomenda escolher valores de polo abaixo de .
- Após arbitrar o valor do polo, posicione o zero através da relação que você encontrou anteriormente;
- Por fim, calcule o ganho do compensador através do critério do módulo. Para um compensador bem projetado, é preciso que o valor do ganho encontrado seja próximo de .
Agora é só seguir a receitinha do bolo e praticar bastante que você vai ficar fera.
O compensador de atraso de fase
Erro em regime permanente
Projeto de um compensador de atraso de fase
Exercícios Resolvidos
Exercício Resolvido #1
Norman N. Nise, Engenharia de sistemas de controle, 6ª ed., Rio de Janeiro, 2012, Questão de Revisão 11
Ao compensar o erro em regime permanente com um compensador de atraso de fase, o que acontece com a resposta transitória.
Passo 1
Vamos lá, nessa questão queremos saber o que acontece com a resposta transitória ao se compensar um erro em regime permanente usando um compensador de atraso de fase.
E na verdade o que vai acontecer é que a resposta transitória permanece praticamente inalterada.
Mas por que isso acontece?
Passo 2
Isso acontece porque o compensador por atraso de fase usa um polo e um zero muito próximos um do outro que faz com que seus efeitos na resposta transitória seja praticamente anulados simultaneamente.
Como usamos valores muito pequenos para o polo e o zero do compensador de atraso de fase, é possível que o zero seja muitas vezes maior que o polo, compensando o erro em regime permanente, ao mesmo tempo que eles estão muito próximos um do outro, não alterando a resposta transitória.
Resposta
A resposta transitória ficará praticamente inalterada, pois o zero e o polo do compensador de atraso de fase são muito próximos, sendo assim o efeito gerado na resposta transitória de um irá anular o efeito do outro e vice versa.
Exercício Resolvido #2
Elaboração própria
Um sistema de realimentação unitária tem função de transferência .
Com o objetivo de reduzir o erro em regime permanente, foi implementado um compensador de atraso com os seguintes parâmetros:
Qual foi o fator de redução do erro dada uma entrada degrau unitário?
Passo 1
O erro antes da compensação é dado por:
Essa fórmula foi deduzida na aula de erro em regime permanente. Se você não se lembra, o estiver interessado em como chegar nela, é só dar uma olhadinha lá.
Passo 2
Com a introdução do compensador, o erro passa a ser calculado da seguinte forma:
Ou seja:
Passo 3
Portanto:
Resposta
Exercício Resolvido #3
Norman N. Nise, Engenharia de sistemas de controle, 6ª ed., Rio de Janeiro, 2012, Exercício 9.1. Adaptado.
Um sistema com realimentação unitária e função de transferência mostrada abaixo está operando com uma resposta em malha fechada que tem overshoot de e tempo de sedimentação para uma faixa de de
- Calcule o erro em regime permanente para uma entrada em rampa unitária.
- Calcule um compensador de atraso de fase para melhorar o erro em regime permanente por um fator de 20.
- Calcule o erro em regime permanente para o sistema compensado.
Passo 1
Primeiramente devemos calcular o erro em regime permanente para o sistema sem compensação.
Para uma entrada rampa, teremos a seguinte expressão para o erro:
Sendo assim:
Passo 2
Devemos agora projetar o compensador que reduzirá esse erro em vinte vezes.
O primeiro passo será encontrar o polo dominante em malha fechada. O polo pode ser encontrado através da expressão:
O fator de amortecimento pode ser encontrado diretamente da fórmula do overshoot:
Para encontrar devemos usar a fórmula do tempo de sedimentação para uma faixa de :
Portanto, o polo dominante será:
Passo 3
Vamos representar no nosso diagrama agora como estamos até aqui.
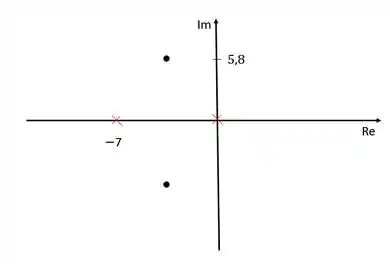
Os “x” vermelhos são os polos em malha aberta da função de transferência, e os pontos pretos são os polos dominantes.
Passo 4
Precisamos agora implementar nosso compensador. Para isso precisamos encontrar a relação entre as posições do zero e do polo.
O objetivo é fazer com que o erro seja reduzido 20 vezes, ou seja
Nesse caso a relação entre polo e zero deu igual ao fator de redução do erro porque se trata de uma trata rampa e a função de transferência é do tipo 1. Nem sempre esses valores coincidirão.
Passo 5
Agora que já sabemos a relação entre a posição do polo e do zero, já podemos posicioná-los.
Sendo assim, devemos arbitrar um valor para o polo e posicionar o zero seguindo a relação que encontramos.
Lembrando que é preciso que ambos os valores sejam bem baixos.Vamos arbitrar:
Passo 6
Por enquanto a função de transferência do compensador está assim:
Só resta então calcular o valor do ganho .
Vamos colocar nossos polos e zeros no diagrama de lugar das raízes para conseguir calcuar o ganho do compensador.
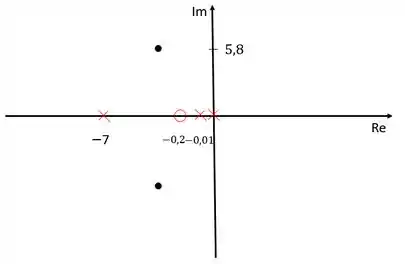
Para calcular o ganho do compensador, devemos usar o critério do módulo, que diz que o produto de todos os módulos é igual a . Sendo que os módulos podem ser calculados como a distância de cada zero/polo ao polo dominante que está repesentado pelo ponto preto.
Os polos dominantes, como nós vimos, ficam em
Sendo assim, precisamos calcular essas distâncias:
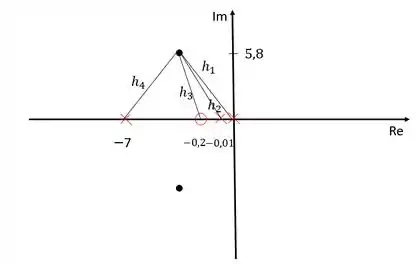
Usando o critério do módulo:
O módulo dos zeros fica no numerador e dos polos no denominador. Precisamos calcular esses módulos agora:
Portanto:
Passo 7
Resposta
Exercício Resolvido #4
Norman N. Nise, Engenharia de sistemas de controle, 6ª ed., Rio de Janeiro, 2012,Problema 3. Adaptado.
Um sistema com realimentação unitária e função de transferência mostrada abaixo está operando com uma resposta em malha fechada que tem overshoot de e tempo de sedimentação para uma faixa de de
- Qual é o valor da constante de erro estático apropriada?
- Obtenha a função de transferência para uma estrutura de atraso de fase de modo que a constante de erro estático seja igual a 4 sem alterar significativamente os polos dominantes do sistema em compensação.
Passo 1
Para calcular a constante de erro, , devemos fazer o limite na função de transferência já que:
Passo 2
Devemos agora projetar o compensador de atraso de fase que produzirá um igual a .
O primeiro passo será encontrar o polo dominante em malha fechada. O polo pode ser encontrado através da expressão:
O fator de amortecimento pode ser encontrado diretamente da fórmula do overshoot:
Para um overshoot de :
Para encontrar devemos usar a fórmula do tempo de sedimentação para uma faixa de :
Portanto, o polo dominante será:
Passo 3
Vamos representar no nosso diagrama agora como estamos até aqui.
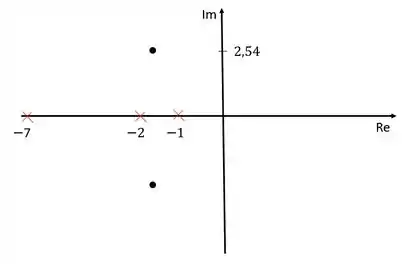
Os “x” vermelhos são os polos em malha aberta da função de transferência, e os pontos pretos são os polos dominantes da resposta.
Passo 4
Precisamos agora implementar nosso compensador. Para isso precisamos encontrar a relação entre as posições do zero e do polo.
Nós queremos que o nosso seja , então:
Passo 5
Agora que já sabemos a relação entre a posição do polo e do zero, já podemos posicioná-los.
Sendo assim, devemos arbitrar um valor para o polo e posicionar o zero seguindo a relação que encontramos.
Lembrando que é preciso que ambos os valores sejam bem baixos.Vamos arbitrar:
Passo 6
Por enquanto a função de transferência do compensador está assim:
Só resta então calcular o valor do ganho .
Vamos colocar nossos polos e zeros no diagrama de lugar das raízes para conseguir calcuar o ganho do compensador.
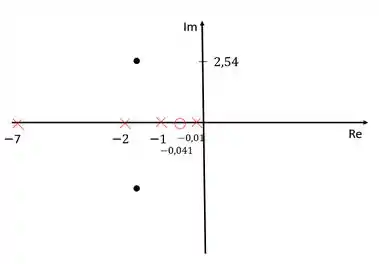
Para calcular o ganho do compensador, devemos usar o critério do módulo, que diz que o produto de todos os módulos é igual a . Sendo que os módulos podem ser calculados como a distância de cada zero/polo ao polo dominante que está repesentado pelo ponto preto.
Os polos dominantes, como nós vimos, ficam em
Sendo assim, precisamos calcular essas distâncias:
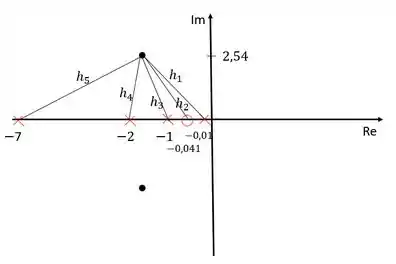
Usando o critério do módulo:
O módulo dos zeros fica no numerador e dos polos no denominador. Precisamos calcular esses módulos agora:
Portanto:
Resposta
Exercício Resolvido #5
Norman N. Nise, Engenharia de sistemas de controle, 6ª ed., Rio de Janeiro, 2012,Problema 4. Adaptado.
Um sistema com realimentação unitária e função de transferência mostrada abaixo está operando com uma resposta em malha fechada que tem overshoot de e tempo de sedimentação para uma faixa de de
- Qual é o valor do erro em estado estacionário para uma entrada rampa unitária?
- Obtenha a função de transferência para uma estrutura de atraso de fase de modo que o erro em estado estacionário seja igual a 0,25 sem alterar significativamente os polos dominantes do sistema em compensação.
Passo 1
A fórmula para o cálculo do erro para uma entrada rampa é essa:
Nós vimos como se chega nessa fórmula na aula de erros em regime permanente, se você tiver dúvida, dá uma olhadinha lá.
Para nossa função de transferência:
Passo 2
Devemos agora projetar o compensador de atraso de fase que produzirá um erro em regime permanente, , igual a .
O primeiro passo será encontrar o polo dominante em malha fechada. O polo pode ser encontrado através da expressão:
O fator de amortecimento pode ser encontrado diretamente da fórmula do overshoot:
Para um overshoot de :
Para encontrar devemos usar a fórmula do tempo de sedimentação para uma faixa de :
Portanto, o polo dominante será:
Passo 3
Vamos representar no nosso diagrama agora como estamos até aqui.
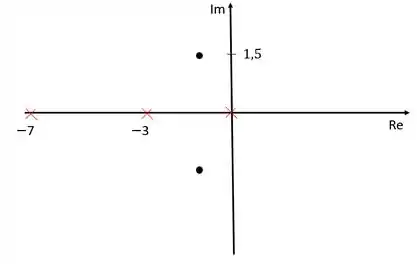
Os “x” vermelhos são os polos em malha aberta da função de transferência, e os pontos pretos são os polos dominantes da resposta.
Passo 4
Precisamos agora implementar nosso compensador. Para isso precisamos encontrar a relação entre as posições do zero e do polo.
Nós queremos que o nosso erro em regime permanente seja então:
Passo 5
Agora que já sabemos a relação entre a posição do polo e do zero, já podemos posicioná-los.
Sendo assim, devemos arbitrar um valor para o polo e posicionar o zero seguindo a relação que encontramos.
Como eles não precisam estar tão afastados um do outro assim, apenas três vezes, podemos escolher um valor para o polo não tão pequeno.Vamos arbitrar:
Passo 6
Por enquanto a função de transferência do compensador está assim:
Só resta então calcular o valor do ganho .
Vamos colocar nossos polos e zeros no diagrama de lugar das raízes para conseguir calcuar o ganho do compensador.
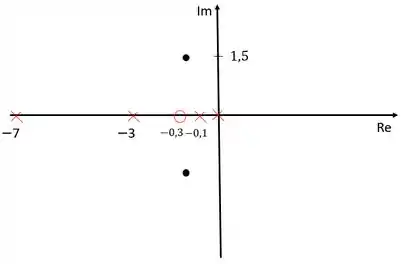
Para calcular o ganho do compensador, devemos usar o critério do módulo, que diz que o produto de todos os módulos é igual a . Sendo que os módulos podem ser calculados como a distância de cada zero/polo ao polo dominante que está repesentado pelo ponto preto.
Os polos dominantes, como nós vimos, ficam em
Sendo assim, precisamos calcular essas distâncias:
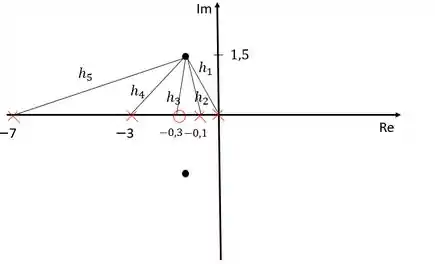
Usando o critério do módulo:
O módulo dos zeros fica no numerador e dos polos no denominador. Precisamos calcular esses módulos agora:
Portanto:
Resposta
Exercício Resolvido #6
Norman N. Nise, Engenharia de sistemas de controle, 6ª ed., Rio de Janeiro, 2012,Problema 5. Adaptado.
Considere um sistema de retroalimentação unitária com função de transferência mostrada abaixo:
Projete um compensador que resultará em sem alterar significativamente a resposta transitória (overshoot de e tempo se sedimentação para uma faixa de de )
Passo 1
Devemos agora projetar o compensador de atraso de fase que produzirá uma constante, igual a .
O primeiro passo será encontrar o polo dominante em malha fechada. O polo pode ser encontrado através da expressão:
O fator de amortecimento pode ser encontrado diretamente da fórmula do overshoot:
Para um overshoot de :
Para encontrar devemos usar a fórmula do tempo de sedimentação para uma faixa de :
Portanto, o polo dominante será aproximadamente:
Passo 2
Vamos representar no nosso diagrama agora como estamos até aqui.
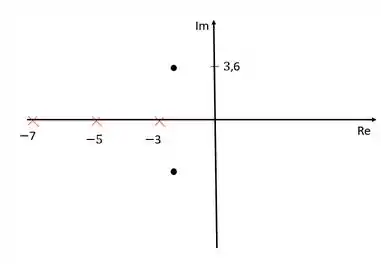
Os “x” vermelhos são os polos em malha aberta da função de transferência, e os pontos pretos são os polos dominantes da resposta.
Passo 3
Precisamos agora implementar nosso compensador. Para isso precisamos encontrar a relação entre as posições do zero e do polo.
Precisamos que o seja iguala a . Com a implementação do compensador, o poderá ser calculado como:
Obs: Para fazer esse cálculo, consideramos o ganho do compensador, , igual a .
Passo 4
Agora que já sabemos a relação entre a posição do polo e do zero, já podemos posicioná-los.
Sendo assim, devemos arbitrar um valor para o polo e posicionar o zero seguindo a relação que encontramos.
Lembre-se que precisamos arbitrar um valor bem pequeno para o polo de modo que o zero e o polo não fiquem muito longe entre si. Uma possibilidade seria:
Passo 5
Por enquanto a função de transferência do compensador está assim:
Só resta então calcular o valor do ganho .
Vamos colocar nossos polos e zeros no diagrama de lugar das raízes para conseguir calcuar o ganho do compensador.
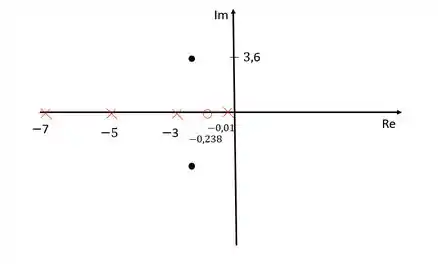
Esse diagrama não está representado com a escala certinha, ok? É só um esboço para a gente ter mais ou menos uma ideia de onde estão as coisas.
Para calcular o ganho do compensador, devemos usar o critério do módulo, que diz que o produto de todos os módulos é igual a . Sendo que os módulos podem ser calculados como a distância de cada zero/polo ao polo dominante que está repesentado pelo ponto preto.
Os polos dominantes, como nós vimos, ficam em
Sendo assim, precisamos calcular essas distâncias:
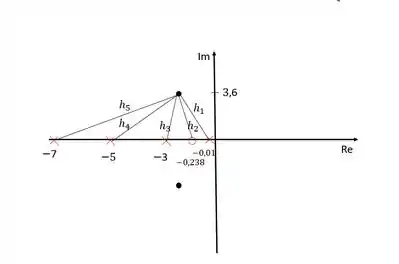
Usando o critério do módulo:
O módulo dos zeros fica no numerador e dos polos no denominador. Precisamos calcular esses módulos agora:
Portanto:
Resposta
Exercício Resolvido #7
Norman N. Nise, Engenharia de sistemas de controle, 6ª ed., Rio de Janeiro, 2012, Exemplo 9.2. Adaptado.
Compense o sistema de retroalimentação unitária com função de transferência mostrada abaixo para melhorar o erro em regime permanente por um fator de 10 vezes para uma entrada degrau, de modo que não altere a resposta transitória do sistema.
Considere que o sistema está operando com polos dominantes em malha fechada em:
Passo 1
O primeiro passo seria fazer a determinação dos polos dominantes em malha fechada. Como o exercício já nos deu de mão beijada essa informação, vamos representar os zeros e polos em malha aberta e os polos dominantes em malha fechada no nosso diagrama.
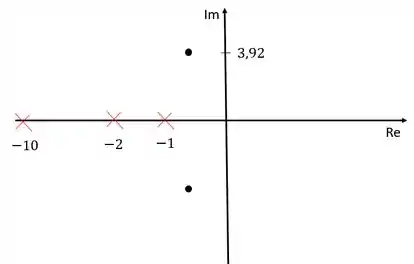
Antes que você me xingue, o desenho não tá feito com a escala certa ok? O importante é só a gente ter uma ideia de como tá o lugar das raízes por enquanto.
Passo 2
O próximo passo é determinar a relação entre o polo e o zero do compensador, já que é isso que fará com que o erro seja reduzido.
Desejamos que o erro seja reduzido dez vezes. Vamos primeiro então calcular o erro sem a presença do compensador
O nosso objetivo adicionando o compensador é que o erro diminua 10 vezes, ou seja, seja de . Para isso:
Passo 3
Agora que já sabemos a relação entre a posição do polo e do zero, já podemos posicioná-los.
Sendo assim, devemos arbitrar um valor para o polo e posicionar o zero seguindo a relação que encontramos.
Lembrando que é preciso que ambos os valores sejam bem baixos. Sendo assim, vamos arbitrar:
Passo 4
Por enquanto a função de transferência do compensador está assim:
Só resta então calcular o valor do ganho .
Vamos colocar nossos polos e zeros no diagrama de lugar das raízes para conseguir calcuar o ganho do compensador.
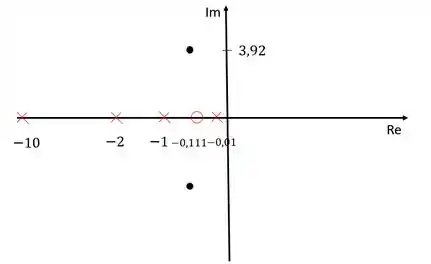
Para calcular o ganho do compensador, devemos usar o critério do módulo, que diz que o produto de todos os módulos é igual a . Sendo que os módulos podem ser calculados como a distância de cada zero/polo ao polo dominante que está repesentado pelo ponto preto.
O polo dominantes, como nós vimos, fica em
Sendo assim, precisamos calcular essas distâncias:
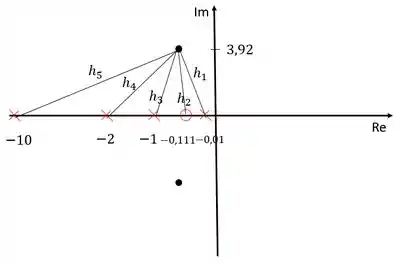
Usando o critério do módulo:
O módulo dos zeros fica no numerador e dos polos no denominador. Precisamos calcular esses módulos agora:
Portanto:
Resposta
Exercício Resolvido #8
LAC – POLI – USP – Capítulo 8 Compensação – Exemplo pag: 11. Adaptado
Considere o sistema cuja função de transferência é:
Projete um compensador de atraso de modo que o fator de amortecimento seja e que o tempo de acomodação para uma porcentagem de seja .
Deseja-se que o erro em regime permanente para uma entrada rampa seja de
Passo 1
Precisamos determinar , e da função de transferência do compensador que satisfaça os critérios do enunciado.
O primeiro passo é definir o polo dominante, e para isso precisamos de e . O valor de já foi dado no enuciado e podemos calcular como abaixo:
O polo dominante pode ser encontrado pela fórmula:
Portanto:
Passo 2
O próximo passo é determinar a relação entre o polo e o zero do compensador, já que é isso que fará com que o erro seja reduzido.
Desejamos um erro de para uma entrada rampa. A equação para calcular o erro para uma entrada rampa é dada abaixo:
A dedução e explicação para essa expressão você encontra na aula de erros em regime permanente. Se você não t[a lembrado, dá uma revisadinha lá.
Substituindo nossas funções de transferência e assumindo que o ganho do compensador é :
Passo 3
Verificamos então que o zero deve ser dez vezes maior que o polo.
Sendo assim, devemos arbitrar um valor para o polo e botar o zero dez vezes maior. Lembrando que é preciso que ambos os valores sejam bem baixos. Sendo assim, vamos arbitrar:
Passo 4
Por enquanto a função de transferência do compensador está assim:
Só resta então calcular o valor do ganho .
Vamos colocar nossos polos e zeros no diagrama de lugar das raízes para conseguir calcuar o ganho do compensador.
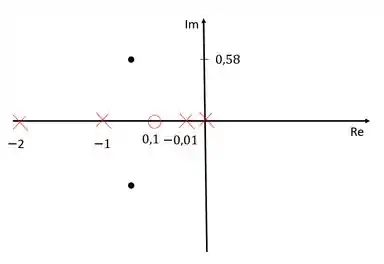
Para calcular o ganho do compensador, devemos usar o critério do módulo, que diz que o produto de todos os módulos é igual a . Sendo que os módulos podem ser calculados como a distância de cada zero/polo ao polo dominante que está repesentado pelo ponto preto.
O polo dominantes, como nós vimos, fica em
Sendo assim, precisamos calcular essas distâncias:
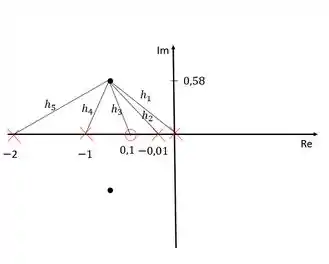
Usando o critério do módulo:
O módulo dos zeros fica no numerador e dos polos no denominador. Precisamos calcular esses módulos agora:
Portanto: