Compensadores de avanço de fase
Produzido por Alexandre NunesTeoria
Introdução
Cada sistema de controle tem a sua própria característica e sua própria dinâmica. Alguns são mais rápidos, alguns são mais estáveis, alguns não apresentam nenhum erro em estado estacionário e outros já apresentam uma grande diferença do valor desejado.
Como cada processo/planta tem sua própria função de transferência, cada um vai ter uma resposta característica diferente a uma perturbação. Entretanto, é possível manipular as características da malha de controle para que a resposta atenda a especificações previamente definidas. Para fazer isso, usamos os compensadores.
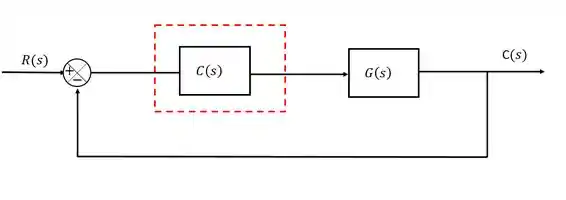
Através dos compensadores, nós adicionaremos polos e zeros à malha de realimentação de forma que a resposta de saída seja alterada. Os compensadores geralmente têm a seguinte função de transferência padrão:
Geralmente, alguns parâmetros como overshoot, tempo de sedimentação e erro em estado estacionário servem como especificações para que seja possível determinar os valores de , e .
Existem três tipos principais de compensadores: compensadores de avanço de fase, compensadores de atraso de fase e compensadores de avanço-atraso de fase. Por enquanto, vamos focar primeiramente nos compensadores de avanço de fase.
Compensadores de avanço de fase
Os compensadores de avanço de fase, também chamados de lead, tem a seguinte função de transferência:
Ou seja, o zero estão sempre mais à direita no eixo dos reais que os polos, em outras palavras, os zero são maiores que os polos. Dessa forma, no diagrama de lugar das raízes, os compensadores de avanço de fase ficam representados da seguinte forma:
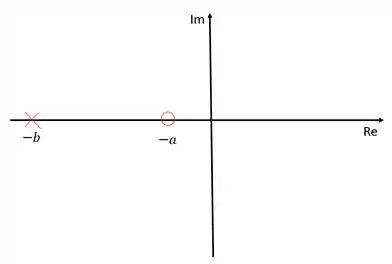
O posicionamento de um zero mais próximo da origem do que o polo faz com que o sistema se torne mais estável, melhorando a margem de estabilidade. Isso significa que o ganho poderá assumir valores maiores sem tornar o sistema instável e também possibilita a diminuição do overshoot e do tempo de acomodação (o sistema fica mais rápido).
Projeto de compensadores de avanço de fase através do método do lugar das raízes
O projeto dos controladores de avanço de fase envolve a determinação do valor do polo e do zero da função de transferência do compensador assim como do ganho. Geralmente, para que se possa fazer essa estimativa, os valores de overshoot, tempo de sedimentação e erro em regime permanente são fornecidos.
O primeiro passo para o projeto do seu compensador é a determinação do seu polo dominante desejado. O polo dominante será o ponto a partir de onde vamos fazer todas as determinações do projeto, e ele pode ser calculado a partir da seguinte fórmula:
Ou seja, para determinar o seu polo dominante, primeiramente você precisa de e e esse valores podem ser encontrados a partir das fórmulas para overshoot e tempo de sedimentação:
Ou seja, com os valores especificados de overshoot e tempo de sedimentação, é possível calcular e , e consequentemente, o polo dominante que você precisa.
Só uma observação: essas fórmulas são para sistemas de segunda ordem. Por isso, quando aplicamos elas a sistemas de ordem superior, estamos considerando que esses sistemas podem ser aproximados por um sistema de segunda ordem. Por isso, muitas vezes na prática, os resultados obtidos pelo método do lugar das raízes gera resultados próximos aos desejados.
Vamos continuar então. O próximo passo é representar os polos dominantes no diagrama de lugar das raízes. Vamos supor que estamos trabalhando com uma função de transferência com dois polos:
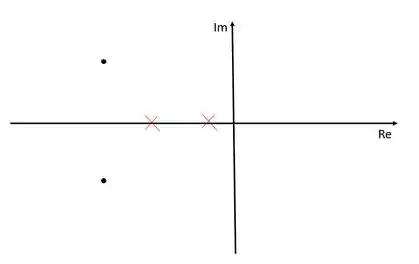
Os “xis” vermelhos representam os polos da função de transferência e os pontos representam os polos dominantes. O nosso objetivo é adicionar o polo e o zero do compensador que faça o diagrama de lugar das raízes passar pelo polo dominante.
Para isso, nós podemos arbitrar qualquer lugar para a colocação do zero e em seguida calcular o lugar do polo no diagrama.
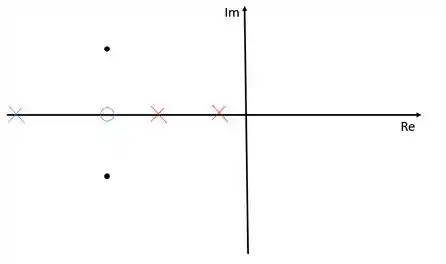
Uma dica é colocar o zero no mesmo ponto na linha dos reais onde se encontram os polos dominantes, isso pode facilitar as contas mais para frente.
Para determinar o polo devemos ligar todos os polos e zeros ao polo dominante:
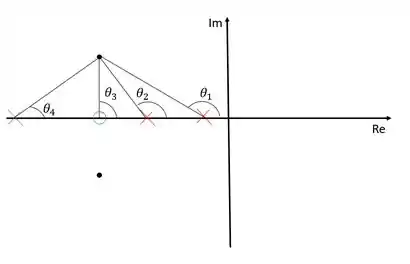
Devemos ligar todos os polos e zeros ao polo dominante e calcular os ângulos formados com o eixo dos reais. Como sabemos a posição dos dois polos da função de transferência, do polo dominante e do zero do compensador que foi arbitrado por nós mesmos, é possível calular , , e através de relações trigonométricas.
A soma de todos os ângulos deve ser um múltiplo ímpar de para que o polo dominante faça parte do lugar das raízes, sendo assim:
Um detalhe: os zeros contribuem com ângulos positivos enquanto os polos contribuem com ângulos negativos.
Uma vez que se encontra o ângulo , é possível encontrar a distância que o mesmo se encontra da origem através de relações trigonométricas.
Para determinar o ganho, usaremos a seguinte regra:
Esse módulo pode ser calculado calculando-se o módulo da distância entre os polos e zeros ao polo dominante.
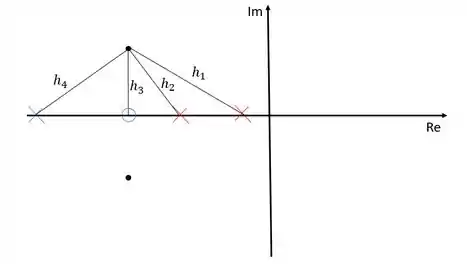
Como os zeros são o numerador e os polos são o denominador, para o caso acima teremos:
Ao final, é sempre bacana dar uma conferida para checar se todas as especificações foram atendidas. Caso alguma coisa tenha ficado um pouco fora da especificação, é válido fazer alguns ajustes finos para deixar tudo dentro do pedido.
Compensadores de avanço de fase
Projeto de compensadores de avanço de fase através do método do lugar das raízes
Exercícios Resolvidos
Exercício Resolvido #1
CESGRANRIO – 2011 – Petrobrás – Engenheiro de equipamento junior - Eletrônica
Um sistema de controle discreto, com realimentação de saída, apresenta uma estrutura de compensação na malha direta, em série com a planta, cuja função de transferência do compensador é
Trata-se do tipo de compensador:
- Avanço de fase
- Atraso de fase
- Derivativo
- Proporcional integral
- PID
Passo 1
Vamos analisar a função de transferência do compensador. Ela tem o formato da função de transferência de avanço de fase olha só:
Precisamo checar a relação entre o polo e o zero.
Passo 2
Para ser considerado compensador de avanço de fase, o zero deve ser maior que o polo.
Nesse caso temos
Logo, o critério foi aceito e a função de transferência é uma função de transferência de compensador de avanço de fase (também chamado de lead)
Resposta
- Avanço de fase
Exercício Resolvido #2
LAC – POLI – USP – Capítulo 8 Compensação – Exemplo pag: 112. Adaptado
Considere um servomecanismo baseado num motor CC controlado pela armadura com função de transferência:
Projete um compensador de avanço de modo que o fator de amortecimento permaneça constante (), porém com tempo de acomodação para tolerância de de .
Passo 1
Precisamos determinar , e da função de transferência do compensador que satisfaça os critérios do enunciado.
O primeiro passo é definir o polo dominante, e para isso precisamos de e . O valor de já foi dado no enuciado e podemos calcular como abaixo:
O polo dominante pode ser encontrado pela fórmula:
Portanto:
Passo 2
Vamos representar os polos da função de transferência em malha aberta e os polos dominantes no diagrama de lugar das raízes
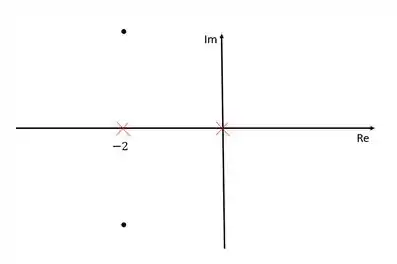
Os dois polos da função de transferência estão representados com um “xis” vermelho e os polos dominantes estão representados pelos pontos. Agora precisamos determinar o polo e o zero do compensador que faça com que o os polos dominantes façam parte do local das raízes. Existem infinitas combinações para esse polo e zero. Sendo assim, vamos arbitrar um valor para o zero e calcular o polo depois a partir desse valor de arbitrado do zero.
Uma tática é colocar o zero sobre o eixo dos reais com o mesmo valor do polo dominante. Nesse caso, o zero do compensador coincidiria com o polo da função de transferência que já existe em . Sendo assim, vamos arbitrar o zero um pouco para a esquerda, em .
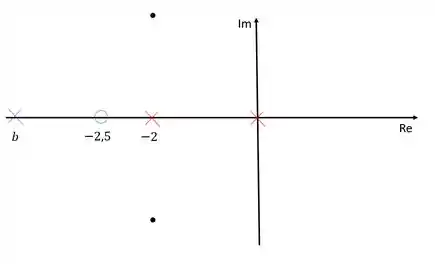
Passo 3
Devemos agora determinar o valor de . Para isso vamos ligar todos os polos e zeros ao polo dominante e calcular o ângulo formado:
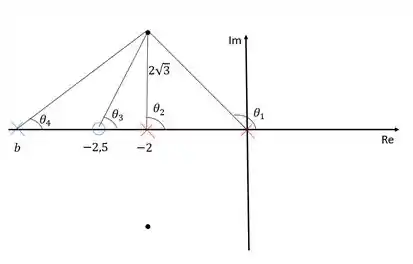
Para conseguir o ângulo , precisamos calcular os ângulos , e . Podemos calcular esses três ângulos utilizando o arcotangentes deles. Então vamos lá:
O ângulo é visto que está na mesma linha horizontal que o polo dominante.
A soma de todos os ângulos dos zeros e polos deve ser um múltiplo ímpar de , então:
Lembrando que os polos contribuem com ângulos negativos e os zeros comângulos positivos, então:
Sabendo o ângulo é possível calcular a localização do polo:
Como é a distância do polo até , o polo se encontrará em .
Passo 4
Por enquanto a função de transferência do compensador está assim:
Só resta então calcular o valor do ganho .
Para calular o ganho, devemos satisfazer a segunte condição:
O módulo dos polos e zeros pode ser obtido calculando-se a distância entre eles e os polo dominante:
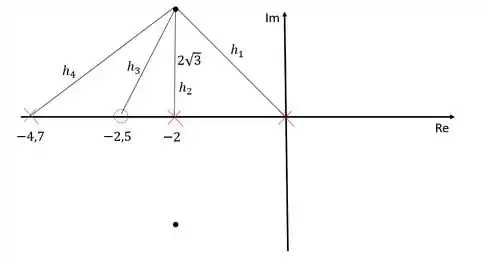
Dessa forma:
Portanto:
Resposta
Exercício Resolvido #3
Unicamp – Professor Fábio Pereira Benjovengo – Lista de exercícios 3 2006.2- Exemplo 01. Adaptado.
Para um sistema realimentado, a função de transferência em malha aberta é:
Projetar um controlador tal que o tempo de sedimentação seja e o overshoot máximo seja de .
Passo 1
Precisamos determinar , e da função de transferência do compensador que satisfaça os critérios do enunciado.
O primeiro passo é definir o polo dominante, e para isso precisamos de e .
Podemos calcular através da fórmula do overshoot:
Para um overshoot de , teremos:
Como o overshoot precisa ser menor que vamos dar uma folguinha e usar um valor um pouco acima do valor encontrado para , dessa forma, garantimos que o overshoot não ultrapassará o limite preestabelecido :
Para achar utilizaremos a expressão para tempo de sedimentação com critério de :
O polo dominante pode ser encontrado pela fórmula:
Portanto:
Passo 2
Vamos representar os polos da função de transferência em malha aberta e os polos dominantes no diagrama de lugar das raízes
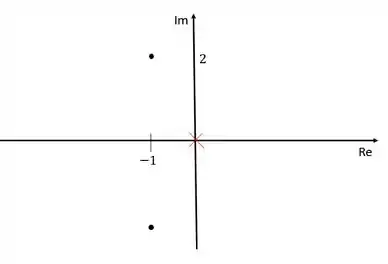
Os dois polos da função de transferência estão representados com um “xis” vermelho. Como os dois polos se encontram na origem, tem apenas um “xis” no gráfico, mas mantenha em mente que são dois polos. Os polos dominantes estão representados pelos pontos.
Agora precisamos determinar o polo e o zero do compensador que faça com que o os polos dominantes façam parte do local das raízes. Existem infinitas combinações para esse polo e zero. Sendo assim, vamos arbitrar um valor para o zero e calcular o polo depois a partir desse valor de arbitrado do zero.
Uma tática é colocar o zero sobre o eixo dos reais com o mesmo valor do polo dominante. Então vamos fazer isso, vamos assumir que o zero se encontra em .
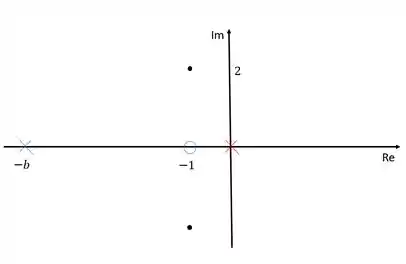
Passo 3
Devemos agora determinar o valor de . Para isso vamos ligar todos os polos e zeros ao polo dominante e calcular o ângulo formado:
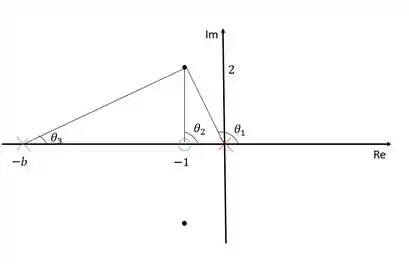
Para conseguir o ângulo , precisamos calcular os ângulos e . Podemos calcular esses dois ângulos utilizando o arcotangente deles. Então vamos lá:
O ângulo é visto que está na mesma linha horizontal que o polo dominante.
A soma de todos os ângulos dos zeros e polos deve ser um múltiplo ímpar de , então:
O ângulo tem que ser considerado duas vezes porque existem dois polos na origem.
Lembrando que os polos contribuem com ângulos negativos e os zeros com ângulos positivos, então:
Sabendo o ângulo é possível calcular a localização do polo:
Como é a distância do polo até , o polo se encontrará em .
Passo 4
Por enquanto a função de transferência do compensador está assim:
Só resta então calcular o valor do ganho .
Para calular o ganho, devemos satisfazer a segunte condição:
O módulo dos polos e zeros pode ser obtido calculando-se a distância entre eles e os polo dominante:
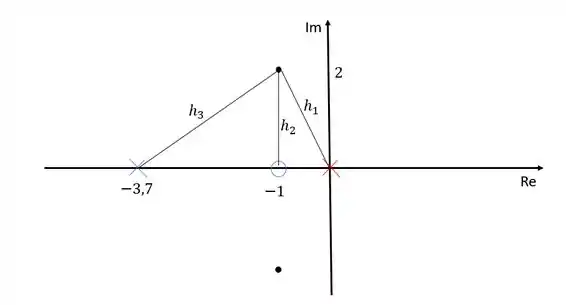
Dessa forma:
Portanto:
O termo referente a distância está ao quadrado devido à presença de dois polos na origem.
Resposta
Exercício Resolvido #4
Unicamp – Professor Fábio Pereira Benjovengo – Lista de exercícios 3 2006.2- Exemplo 05. Adaptado.
Considere um sistema de controle em malha fechada com realimentação unitária e função em malha aberta dada por:
Utilizar o método do lugar das raízes para projetar um compensador na forma:
Tal que o sistema em malha fechada apresente os polos dominantes em . Assuma .
Passo 1
Esse exercício já nos é fornecido no enunciado o local dos polos dominantes em malha fechada. Sendo assim, não precisamos calcular e , podemos partir direto para o esboço do lugar das raízes.
Vamos representar no lugar das raízes os três polos em malha aberta e os polos dominantes:
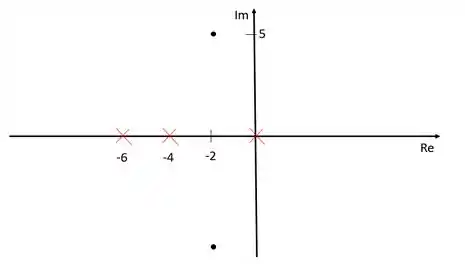
Passo 2
O próximo passo seria arbitrar um ponto para o zero e encontrar um polo que faça com que o lugar das raízes passe pelos polos dominantes. Entretanto, não precisamos arbitrar esse ponto porque o enunciado pede que . Então vamos colocar o zero e polo do compensador no diagrama:
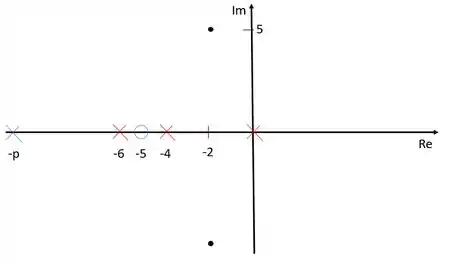
Passo 3
Devemos agora determinar o valor de . Para isso vamos ligar todos os polos e zeros ao polo dominante e calcular o ângulo formado:
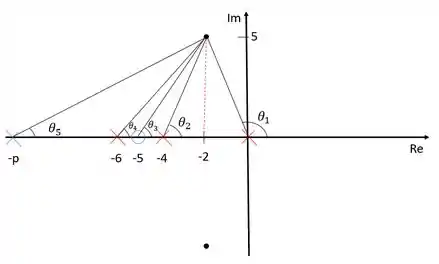
A linha pontilhada vermelha foi desenhada apenas para auxiliar a visualização das relações trigonométricas no plano.
Para conseguir o ângulo , precisamos calcular os ângulos , , e . Podemos calcular esses ângulos utilizando o arcotangentes deles. Então vamos lá:
A soma de todos os ângulos dos zeros e polos deve ser um múltiplo ímpar de , então:
Lembrando que os polos contribuem com ângulos negativos e os zeros comângulos positivos, então:
Conhecendo o ângulo é possível calcular a localização do polo:
Como é a distância do polo até , o polo se encontrará em .
Passo 4
Por enquanto a função de transferência do compensador está assim:
Só resta então calcular o valor do ganho .
Para calular o ganho, devemos satisfazer a segunte condição:
O módulo dos polos e zeros pode ser obtido calculando-se a distância entre eles e os polo dominante:
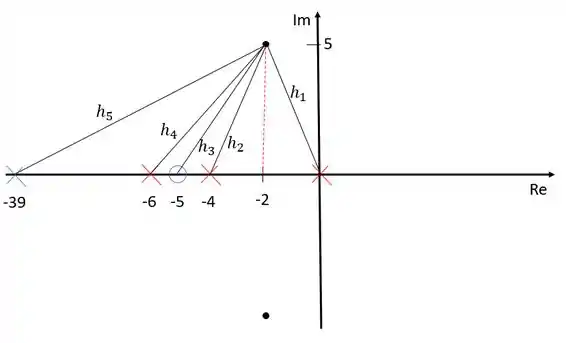
Dessa forma:
Portanto:
Resposta
Exercício Resolvido #5
Norman N. Nise, Engenharia de sistemas de controle, 6ª ed., Rio de Janeiro, 2012, Exercício 9.2. Adaptado
Um sistema com realimentação untária e a seguinte função de transferência abaixo está operando com de overshoot.
- Calcule o tempo de acomodação para um critério de
- Projete um compensador de avanço de fase para reduzir o tempo por um fator de . Escolha o zero do compensador em .
Passo 1
Para calular o tempo de acomodação para um critério de usaremos a seguinte fórmula:
Precisamos então determinar e .
pode ser obtido através da fórmula do overshoot. Como nós sabemos que o overshoot é conseguimos determinar o fator de amortecimento então:
A frequência crítica é possível determinar através da função de transferência. Numa função de transferência de segunda ordem, a constante que multiplica o fator é igual a . Portanto:
Portanto, o tempo de sedimentação será:
Passo 2
Agora precisamos projetar um compensador que diminua o tempo de sedimentação em três vezes e mantenha o fator de amortecimento (mesmo overshoot). Para isso, devemos determinar , e K da função de transferência do compensador que satisfaça os critérios do enunciado.
O primeiro passo é definir o polo dominante, e para isso precisamos de e .
Como desejamos manter o overshoot igual, não iremos alterar o gator de amortecimento considerar:
Já que desejamos reduzir o tempo de sedimentação em três vezes mantendo o fator de amortecimento constante, a frequência crítica deve ser o triplo:
O polo dominante pode ser encontrado pela fórmula:
Portanto:
Passo 3
Vamos representar os polos da função de transferência em malha aberta e os polos dominantes no diagrama de lugar das raízes
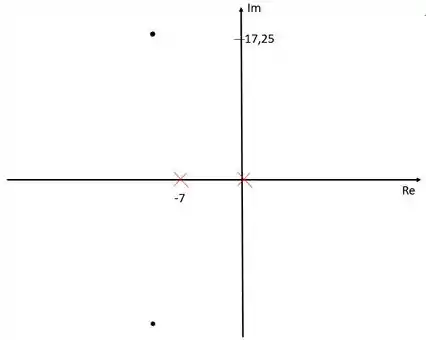
Os dois polos da função de transferência estão representados com um “xis” vermelho. Os polos dominantes estão representados pelos pontos.
Agora precisamos determinar o polo e o zero do compensador que faça com que o os polos dominantes façam parte do local das raízes. Caso o exercício não tivesse sugerido um ponto para o zero nós poderíamos arbitrar esse ponto. Entretanto, foi pedido que usássemos como o zero do controlador.
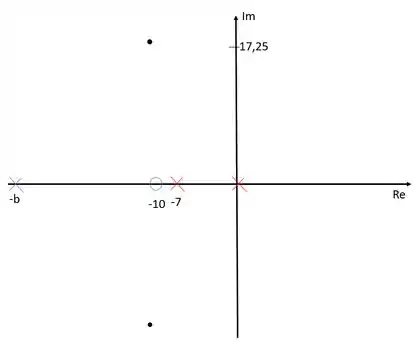
Passo 4
Devemos agora determinar o valor de . Para isso vamos ligar todos os polos e zeros ao polo dominante e calcular o ângulo formado:
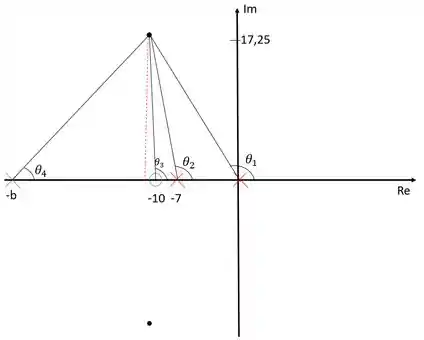
A linha pontilhada vermelha foi traçada apenas para ajudar na visualização das identidades trigonométricas. Os polos dominantes tem valor real e imaginário .
Para conseguir o ângulo , precisamos calcular os ângulos , e . Podemos calcular esses três ângulos utilizando o arcotangente deles. Então vamos lá:
A soma de todos os ângulos dos zeros e polos deve ser um múltiplo ímpar de , então:
Lembrando que os polos contribuem com ângulos negativos e os zeros com ângulos positivos, então:
Sabendo o ângulo é possível calcular a localização do polo:
Como é a distância do polo até , o polo se encontrará em .
Passo 5
Já temos o polo e o zero do compensador, agora só falta o ganho.
Só resta então calcular o valor do ganho .
Para calular o ganho, devemos satisfazer a segunte condição:
O módulo dos polos e zeros pode ser obtido calculando-se a distância entre eles e os polo dominante:
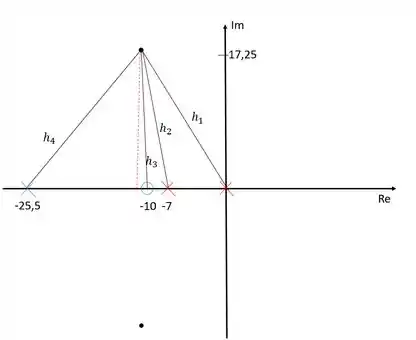
Dessa forma:
Portanto:
Resposta
Exercício Resolvido #6
Norman N. Nise, Engenharia de sistemas de controle, 6ª ed., Rio de Janeiro, 2012, Problema 9. Adaptado.
Considere um sistema com realimentação unitária função de transferência do processo:
- Determine a posição dos polos dominantes para resultar em um tempo de acomodação de e emum overshoot de .
- Se um compensador com o zero em for utilizado para alcançar as condições do item a), qual deve ser a contribuição angular do polo do compensador?
- Determine a posição do polo do compensador.
- Determine o ganho necessário para atender aos requisitos declarados no item a).
Passo 1
Para determinar a posição dos polos dominantes para as especificações dadas, precisamos calcular e que tornam esses requisitos verdadeiros. Uma vez que obtemos esses valores, os polos dominantes podem ser calculados pela fórmula:
Podemos calcular através da fórmula do overshoot:
Para um overshoot de , teremos:
Para achar utilizaremos a expressão para tempo de sedimentação com critério de :
Os polos dominantes são portanto:
Passo 2
O item b) pede que seja calculado a contribuição de ângulo do polo de um compensador projetadopara atingir essas condições e com zero em . Vamo representar tudo isso no diagrama de lugar das raízes então:
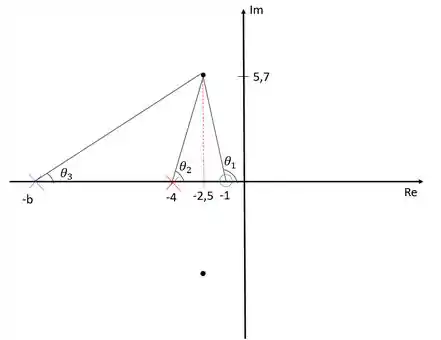
Para definir o ângulo , precisamo primeiro descobrir e . Sendo assim:
No lugar das raízes, a soma de todos os ângulo feitos entre os zeros e polos e qualquer ponto por onde passa o lugar das raízes deve ser um múltiplo ímpar de . Como desejamos que o lugar das raízes passe pelo nosso polo dominante, a soma de todas os ângulos deve satistafzer essa igualdade.
Obs: O ângulo é multiplicado por três porque o polo em é de terceira ordem.
Passo 3
Para determinar a posição do polo, utilizaremos a tangente do módulo ângulo :
Como é a distância entre o polo e o ponto , o polo estará em .
Passo 4
Para calular o ganho, devemos satisfazer a segunte condição:
O módulo dos polos e zeros pode ser obtido calculando-se a distância entre eles e os polo dominante:
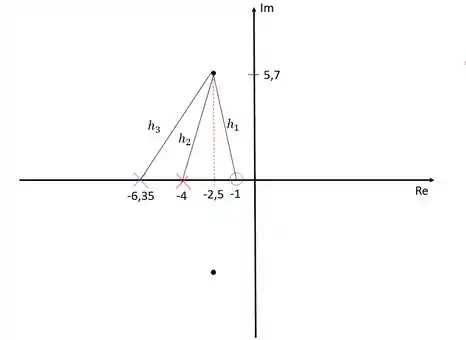
Dessa forma:
Sendo assim:
está elevado ao cubo, devido ao fato de o polo em ser de terceira ordem.
Portanto:
Resposta
Exercício Resolvido #7
Norman N. Nise, Engenharia de sistemas de controle, 6ª ed., Rio de Janeiro, 2012, Problema 9.13. Adaptado.
Para um sistema realimentado, a função de transferência em malha aberta é:
O sistema está operando com de overshoot e tempo de sendimentação para um critério de de . Determine os polos dominantes e o polo, zerp e ganho do compensador para que o sistema diminua o tempo de acomodação pela metade mantendo-se o mesmo percentual de overshoot.
Passo 1
Para definir o polo dominante, precisamo de e :
Podemos calcular através da fórmula do overshoot:
Para um overshoot de , teremos:
Para achar utilizaremos a expressão para tempo de sedimentação com critério de :
O polo dominante pode ser encontrado pela fórmula:
Portanto:
Passo 2
Vamos representar os polos da função de transferência em malha aberta e os polos dominantes no diagrama de lugar das raízes
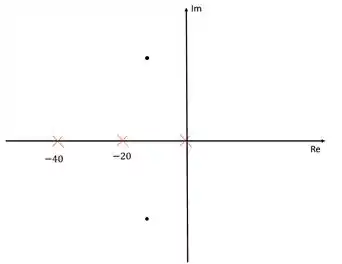
Os polos da função de transferência estão representados com um “xis” vermelho. Os polos dominantes estão representados pelos pontos.
Agora precisamos determinar o polo e o zero do compensador que faça com que o os polos dominantes façam parte do lugar das raízes. Existem infinitas combinações para esse polo e zero. Sendo assim, vamos arbitrar um valor para o zero e calcular o polo depois a partir desse valor de arbitrado do zero.
Uma tática é colocar o zero sobre o eixo dos reais com o mesmo valor do polo dominante. Então vamos fazer isso, vamos assumir que o zero se encontra em . Outra tática é colocar o zero no mesmo lugar que algum polo do processo de forma que o zero e o polo se cancelem. Vamos adotar essa estratégia e colocar o zero em . O polo e zero irão se cancelar e vamos ficar com a seguinte situação:
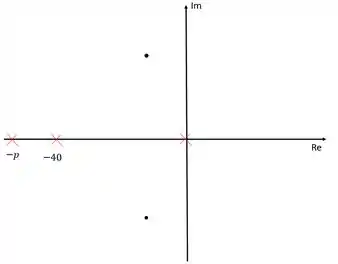
Passo 3
Devemos agora determinar o valor de . Para isso vamos ligar todos os polos e zeros ao polo dominante e calcular o ângulo formado:
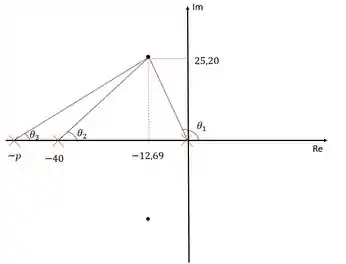
Para conseguir o ângulo , precisamos calcular os ângulos e . Podemos calcular esses dois ângulos utilizando o arcotangente deles. Então vamos lá:
A soma de todos os ângulos dos zeros e polos deve ser um múltiplo ímpar de , então:
Lembrando que os polos contribuem com ângulos negativos e os zeros com ângulos positivos, então:
Sabendo o ângulo é possível calcular a localização do polo:
Como é a distância do polo até , o polo se encontrará em .
Passo 4
Só resta então calcular o valor do ganho .
Para calular o ganho, devemos satisfazer a segunte condição:
O módulo dos polos e zeros pode ser obtido calculando-se a distância entre eles e os polo dominante:
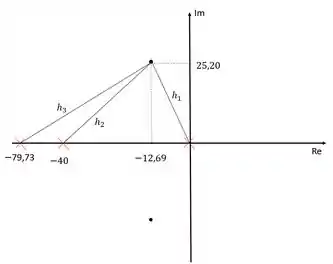
Obs: a figura não está representada em escala.
Dessa forma:
Portanto:
Resposta
Polos dominantes:
Função de transferência do compensador:
Exercício Resolvido #8
Elaboração própria
Considerando a função de transferência do processo abaixo:
Projete um compensador de avanço de fase de modo que o overshoot máximo seja e o tempo de sedimentação para um critério de seja .
Passo 1
O pimeiro passo para projetar o compensador é definir umpar depolos dominantes de malha fechada que atenda às necessidade requeridas. Para definir o polo dominante, precisamo de e :
Podemos calcular através da fórmula do overshoot:
Para um overshoot de máximo de , teremos:
Fazer o projeto com o fator de amortecimento no limite é um pouco arriscado, visto que essas equações são aproximações e o resultado final pode variar um pouco. Sendo assim, vamos dar uma folguinha para o fator de amortecimento e usar:
Para achar utilizaremos a expressão para tempo de sedimentação com critério de :
O polo dominante pode ser encontrado pela fórmula:
Portanto:
Passo 2
Vamos representar os polos da função de transferência em malha aberta e os polos dominantes no diagrama de lugar das raízes
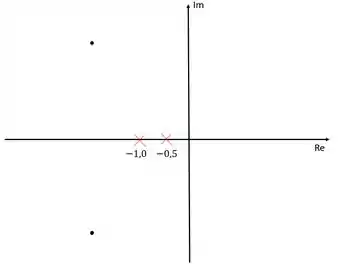
Os polos da função de transferência estão representados com um “xis” vermelho. Os polos dominantes estão representados pelos pontos.
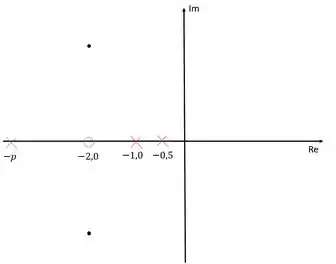
Agora precisamos determinar o polo e o zero do compensador que faça com que o os polos dominantes façam parte do lugar das raízes. Existem infinitas combinações para esse polo e zero. Sendo assim, vamos arbitrar um valor para o zero e calcular o polo depois a partir desse valor de arbitrado do zero.
Uma tática é colocar o zero sobre o eixo dos reais com o mesmo valor do polo dominante. Então vamos fazer isso, vamos assumir que o zero se encontra em . Vamos fazer usando essa tática então:
Passo 3
Devemos agora determinar o valor de . Para isso vamos ligar todos os polos e zeros ao polo dominante e calcular o ângulo formado:
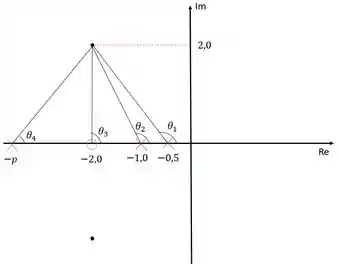
Para conseguir o ângulo , precisamos calcular os ângulos , e . Podemos calcular esses ângulos utilizando o arcotangente deles. Então vamos lá:
Como está diretamente abaixo do polo dominante:
A soma de todos os ângulos dos zeros e polos deve ser um múltiplo ímpar de , então:
Lembrando que os polos contribuem com ângulos negativos e os zeros com ângulos positivos, então:
Sabendo o ângulo é possível calcular a localização do polo:
Como é a distância do polo até , o polo se encontrará em .
Passo 4
Só resta então calcular o valor do ganho .
Para calular o ganho, devemos satisfazer a segunte condição:
O módulo dos polos e zeros pode ser obtido calculando-se a distância entre eles e os polo dominante:
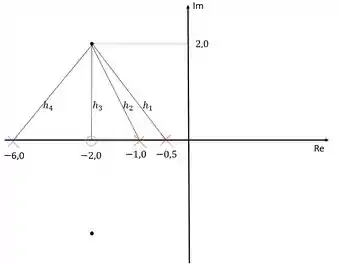
Obs: a figura não está representada em escala.
Dessa forma:
Portanto:
Os zeros ficam no numerador e os polos no denominador: