Controlador proporcional-integrativo
Teoria
Introdução
Até agora nós conhecemos um pouco dos dois modelos mais básicos de controladores: o controlador liga/desliga e o controlador proporcional.
Só para relembrar um pouco desses dois controladores, o controlador liga/desliga está sempre em seu modo máximo ou em seu modo mínimo. Quando a variável controlada excede muito o setpoint o controlador entra no seu modo desligado, tendo como sinal de saída o mínimo possível. Quando a variável controlada está muito abaixo do setpoint, o contrário acontece e o controlador emite sinal máximo para o elemento final de controle. Sendo assim, a variável manipulada está sempre nos arredores do setpoint mas nunca se estabiliza no mesmo.
O controlador proporcional responde de maneira proporcional ao erro do sistema. Essa proporcionalidade é ditada pelo ganho do controlador . O controlador proporcional sempre deixa erro residual para o caso de uma entrada degrau.
Então esses dois controladores são os mais simples e baratos, e por isso são os mais comumente usados na indústria. Entretanto, para alguns casos onde o controle precisa ser feito com mais rigor, eles não serão suficientes, principalmente pelo fato de não fazerem com que a variável controlada se estabilize no setpoint.
Foi para ajudar nessas situações que surgiu nosso grande amigo controlador proporcional-integrativo (mas pode chamar de PI). Vamos então entender um pouco melhor como ele funciona, quais são seus parâmetros e por que ele é tão pica das galáxias.
Controlador proporcional-integrativo (PI)
Todos os controladores recebem uma informação sobre o erro do sistema, , e respondem com um sinal de saída, , baseado nesse erro.
Para o controlador proporcional-integrativo, a função no domínio tempo para o sinal de saída do controlador é definida como:
Ou ainda, no domínio da frequência (aplicando transformada de Laplace):
Logo de cara, podemos perceber que o controlador proporcional integral possui dois termos, e um a mais que o controlador proporcional. Isso por si só já o torna mais robusto e sofisticado.
continua sendo o ganho do controlador, ele funciona da mesma maneira que o ganho do controlador proporcional. é a constante de tempo integral e ele vai ser o principal responsável pela ação integrativa do controlador.
Vamos analisar melhor como esses termos impactam na resposta do controlador olhando o gráfico abaixo:
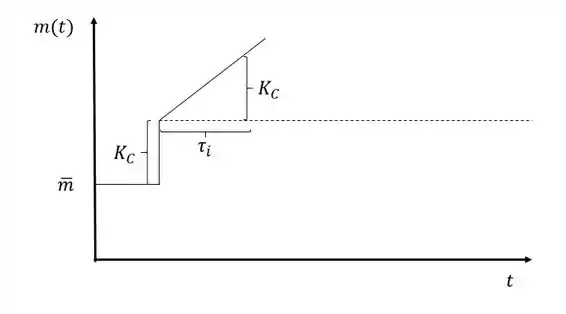
Esse é o gráfico do sinal de saída do controlador, , após uma entrada do tipo degrau unitário.
Vamos analisar bem o que esse gráfico está querendo nos dizer. Primeiramente podemos perceber que como estamos trabalhando com um controlador do tipo PI nós podemos notar os efeitos da ação proporcional e da ação integrativa. A ação proporcional é responsável pelo degrau no momento em que a perturbação ocorreu. Esse degrau terá magnitude . Já a ação integrativa é responsável pela rampa que vem em sequência. Isso pode ser visto também analisando a equação do controlador:
Fazendo:
seria então o valor inicial quando o sistema não apresenta nenhum erro, é o degrau causado pela perturbação degrau e derivado da ação proporcional do controlador. E por fim é o coeficiente de inclinação da reta causada pela parte integrativa. Sendo que é o tempo que se passou para que ocorresse uma elevação de magnitude no sinal de saída do controlador.
Ou seja, quanto
O efeito da parte integrativa do controlador será mais fortemente sentido quanto maior for a inclinação da reta. O coeficiente de inclinação da reta aumenta com o aumento de e com a diminuição de .
Em alguns lugares, podemos ver a função de transferência para o controlador PI escrita da seguinte forma:
Dessa forma, é chamado de ganho integral, e comparando com a versão apresentada primeiramente, ele seria:
Por que o controlador PI anula o erro
A principal vantagem do controlador PI em relação aos controladores que não possuem a parcela integralizadora é que esse tipo de controlar não apresenta offset para entradas do tipo degrau.
Isso acontece devido ao fato de que a função de transferência apresenta um termo com polo na origem, fazendo com que ela seja do tipo 1:
Repare que quando rearranjamos a função de transferência do controlador PI, ela apresenta um polo na origem e um zero em .
Esse polo na origem faz com que a função de transferência seja do tipo 1. Caso você não se lembre bem dessa classificação, sugiro que dê uma revisada na aula de erros em regime permanente.
Ainda nessa aula, nós vimos que sistemas do tipo 1 apresentam erros nulos em regime permanente para entradas do tipo degrau.
Essa então é a grande vantagem do controlador PI. Ele transforma sistemas com processos do tipo 0 em sistemas do tipo 1. Caso o processo já seja do tipo 1, ele transformará o sistema em um sistema do tipo 2, e assim por diante.
Mas então pode vir a dúvida: “se o que faz com que o erro seja nula é o polo na origem, porque não ter um controlador só integral?”
Boa pergunta, jovem. O polo na origem apesar de fazer com que o erro em estado estacionário seja zero, ele também aumenta significativamente a instabilidade do sistema. Dessa forma, a parte proporcional gera um zero negativo no sistema que faz com que ele seja mais estável.
Quanto menor for maior será a predominância da parte integrativa e mais instável o sistema será. Já valores muito grandes de fazem com que a parte proporcional seja predominante e que o tempo para se atingir o valor do estado estacionário seja maior.
Controlador proporcional-integrativo (PI)
Por que o controlador PI anula o erro
Exercícios Resolvidos
Exercício Resolvido #1
Petrobrás – Técnico de Manuntenção Junior – Instrumentação (CESGRANRIO – 2012)
Em um sistema de controle realimentado com um controlador PI, o(a):
- Aumento do ganho integral sem alteração no ganho proporcional nunca instabiliza o sistema;
- Aumento do ganho proporcional reduz o tempo de subida, mas aumenta o desvio de offset para uma entrada do tipo degrau;
- Aumento do ganho proporcional aumenta o tempo de subida e tende a instabilizar o sistema;
- Aumento do ganho derivativo reduz o tempo de subida;
- Parcela integral elimina o desvio de offset para uma entrada do tipo degrau.
Passo 1
Vamos analisar uma de cada vez
A primeira alternativa diz que o aumento do ganho integral sem alterações no ganho proporcional não instabiliza o sistema.
Essa afirmativa é falsa, o aumento no ganho integral faz com que a parcela integral seja predominante no controlador deixando o sistema altamente instável.
Passo 2
A segunda alternativa diz que o aumento do ganho proporcional reduz o tempo de subida, mas aumenta o desvio de offset para uma entrada degrau.
Essa afirmativa é parcialmente correta, o aumento de realmente diminui o tempo de subida, entretanto, também diminui o erro no offset para uma entrada degrau.
Sendo assim, essa alternativa também é falsa.
Passo 3
A terceira alternativa também é parcialmente correta.
Como vimos na alternativa anterior, o aumento do ganho proporcional aumenta o tempo de subida, então a primeira parte da afirmação está incorreta, apesar da segunda parte que diz que o aumento do ganho proporcional causa instabilidade estar correta.
A terceira afirmativa também é falsa, então.
Passo 4
A quarta afirmativa é completamente incorreta visto que o controlador PI nem sequer possui parcela derivativa, portanto, não apresenta ganho derivativo.
Portanto, a alternativa é falsa.
Passo 5
Sendo assim, a alternativa e) é a alternativa verdadeira.
De fato, a parcela integral no controlador PI é a grande responsável pela eliminação do erro em estado estacionário.
Sendo assim, a afirmativa é verdadeira.
Resposta
e) Parcela integral elimina o desvio de offset para uma entrada do tipo degrau.
Exercício Resolvido #2
PETROQUIMICA SUAPE – Supervisor de produção – CESGRANRIO - 2011
Um controlador que processa, simultaneamente, APENAS o sinal de erro instantâneo e o erro acumulado ao longo do tempo é do tipo:
- Proporcional Derivativo
- Proporcional
- Proporcional Integral Derivativo
- Proporcional Integral
- Proporcional Diferencial Derivativo
Passo 1
Como vimos, a expressão para o controlador proporcional integral é:
Como podemos ver pela fórmula, representa o sinal quando não existe erro, a segunda parcela é a responsável por compensar o erro instantâneo e a terceira parcela integra todo o erro acumulado.
Logo, a resposta é:
d) Proporcional Integral
Resposta
d) Proporcional Integral
Exercício Resolvido #3
Aeronáutica – 2014 – CIAAR – Engenharia Eletrônica
Um sistema realimentado com um controle proporcionalapresenta 5% de erro de offset para uma entrada degrau. Para eliminar totalmente o erro de offset, é necessário:
- Aumentar o ganho proporcional.
- Inserir uma ação integral no controlador.
- Inserir uma ação derivativa no controlador.
- Utilizar um controle feedforward em malha aberta.
Passo 1
O aumento do ganho proporcional diminui, de fato, o erro de offset, mas ele por si só não é capaz de eliminar completamente esse erro.
A ação derivativa não causa nenhum impacto no offset e a malha feedforward não está relacionada em nada com o nosso objetivo.
A inserção da parcela integral, sim, elimina o erro de offset totalmente, devido ao fato de ela aumentar o tipo do sistema fazendo com que perturbações do tipo degrau possam ser completamente anuladas.
Resposta
b) Inserir uma ação integral no controlador.
Exercício Resolvido #4
2017 – IFB – Professor- Área de Engenharia Elétrica – Prova 58387
Qual é o erro em regime permanente do sistema de controle a seguir se o controlador utilizado for do tipo proporcional integral (PI) com constantes , , e a entrada for do tipo degrau?
- 3
- 0
- I
- 0,25
- 0,75
Passo 1
Essa é aquele tipo de questão maliciosa que quer te induzir ao erro.
Nessa questão temos um processso de primeira ordem, e um controlador PI. O enunciado nos dá os valores dos ganhos proporcional e integral e pede que a gente diga qual será o erro no estado estacionário para uma entrada degrau.
Entretanto, sabemos que um controlador PI sempre anula o erro em estado estacionário se a entrada for do tipo degrau. Sendo assim, pouco importa o valor das constantes ou a função de transferência do processo, a resposta será sempre .
Resposta
b)
Exercício Resolvido #5
SENAI – Fundamentos de Controle de Processos – 1999 – pag. 43 – Exercício 4. Adaptado
Um controlador PI é sensibilizado em um determinado instante por um desvio de . Considerando que este controlador se encontra em uma bancada de teste (malha aberta), calcular a nova saída segundos após ter sido introduzido o desvio, sabendo-se que:
Faixa Proporcional = 60%
Ganho Integral = 2 rpm ( repetições por minuto )
Ação do Controlador reversa
Saída anterior:
Passo 1
Vamos usar a fórmula pra o controlador PI:
Ou:
Nós já temos , que é .
Para calcular devemos usar a banda proporcional que foi dada:
Como a ação é reversa, o ganho é positivo.
Passo 2
Agora é só jogar na fórmula:
O ganho integral, foi dividido por devido à conversão de minutos para segundos.
Sendo assim:
Resposta
Exercício Resolvido #6
Elaboração própria
Um controlador PI se encontra em malha aberta. Quando o sinal de erro de entrada é sua sáida é . Ele é então sensibilizado por um erro de e após, o sinal de saída do controlador é de . Calcule seu ganho proporcional sabendo que
Passo 1
Vamos usar a fórmula pra o controlador PI:
Nós já sabemos que:
Passo 2
Sendo assim, é só jogar tudo na fórmula:
Resposta
Exercício Resolvido #7
Professor Lizandro Sousa, UFF, lista 4, 2019.2. Questões Extras - Exercício 1
A entrada de um controlador PI sofre uma modificação degrau do tipo C(s) = 2/s , onde C(s) é a variável controlada, e a saída do controlador (em relação ao estado estacionário) muda inicialmente conforme ilustrado na Figura seguinte. De acordo com a figura, estime os valores do ganho do controlador 𝐾𝐶 e a constante de tempo integral τ𝑖 . Considere que o set-point é fixo.
Passo 1
Para resolver essa questão bem rapidinho, vamos comparar o gráfico do enunciado, com esse gráfico aqui:
Esse gráfico é o gráfico da saída do controlado PI para uma resposta do tipo degrau unitário.
Passo 2
Pelo gráfico podemos perceber que é a variação no sinal no momento da perturbação. Entretanto, para o gráfico acima, a entrada foi um degrau unitário, já para o nosso exemplo, a entrada teve magnitude , sendo assim:
Mas, podemos perceber também que o controlador é do tipo direto, já que o um degrau positivo causou um aumento do sinal, sendo assim:
Passo 3
Pelo gráfico, também podemos perceber que a inclinação da reta é dada pela razão entre o ganho e a constante de tempo de integração. Então:
Novamente dividimos por devido à amplitude do degrau.
Resposta
Exercício Resolvido #8
Elaboração própria
Mostre porque um contralador do tipo PI anula o erro em regime estacionário para um processo de ordem e uma entrada do tipo degrau unitário no distúrbio.
Passo 1
Vamos tentar esboçar um diagrama de blocos genérico para a situação acima:
Nesse caso, é a variável controlada, é a referência (setpoint), o distúrbio.
A função de transferência é a função de transferência do controlador proporcional integral:
E a função de trsnferência é um processo qualquer de ordem . Vamos continuar nos referinda a ela como somente .
Passo 2
Sendo assim vamos tentar calcular a expressão para o erro nesse sistema e em seguida calcular o erro em regime permanente utilizando o teorema do valor final.
Pelo diagrama de blocos temos:
Substituindo a segunda na primeira:
Por fim:
Passo 3
Agora que já temos a expressão do erro podemos começar a substituir as nossas funções.
Como a variação foi no distúrbio e não no setpoint, temos que:
Portanto:
Como é o nosso PI:
Então:
Passo 4
Aplicando o teorema do valor final:
Logo:
Multiplicando em cima e embaixo por :
Dessa forma, se a função for do tipo , o erro então também será visto que o termo que tende a zero no denominador não vai poder ser simplificado. Então, aplicando o limite:
Resposta
Ei, a resposta está no passo a passo :)