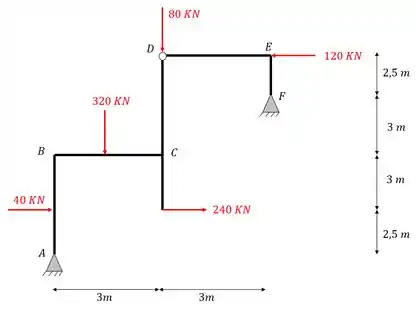
Calcule o equilíbrio dos nós E e B do pórtico abaixo.
Passo 1
Para resolvermos qualquer exercício de pórticos simples, precisamos seguir uma sequência de passos que irá nos ajudar na solução desse tipo de problema, e a sequência é a seguinte.
- A primeira coisa que devemos fazer é o cálculo das reações de apoio, pois assim conseguiremos calcular qualquer nó sem que haja nenhum problema.
- a segunda coisa é seguir a seguinte sequência de nós a serem resolvidos:
Nós com 2 barras
Nós com 3 barras
Nós com 4 barras
...
- A terceira coisa que devemos fazer é calcular o valor dos momentos fletores, cortantes e normais em todos as barras que chegarem ou saírem de algum nó
- O quarto e último passo consiste em desenhar os diagramas do pórtico quando esse for pedido.
Agora que já sabemos qual sequência de passos devemos seguir, vamos aplicar esse conhecimento ao nosso problema.
Passo 2
Como vimos, a primeira coisa que devemos fazer é determinar as reações de apoio, para isso, primeiro iremos trocar os apoios por vetores reações de apoio, como indica a figura abaixo.
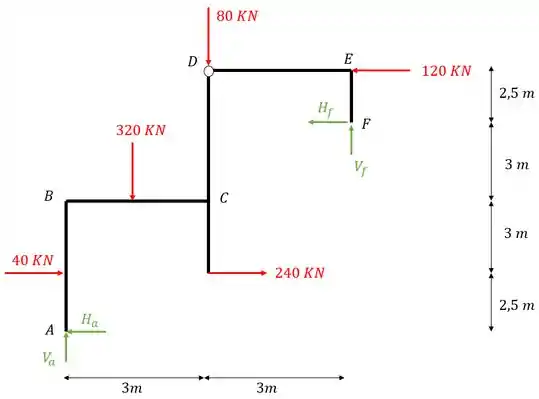
Agora que já temos os vetores e medidas, vamos fazer o equilíbrio de equações
E lembre-se que as rótulas também fornecem equações, e nesse caso, a equação que ela fornece é de que o somatório de momentos fletores nela, vindo pela esquerda ou pela direita, tem que ser, obrigatoriamente, zero, com isso, se fizermos o somatório de momentos fletores em D vindo pela direita, teremos que
Logo
Relacionando os sistemas teremos que
logo
Isolando teremos
Isolando do outro sistema teremos que
Tendo os valores de e basta substituirmos no terceiro sistema, que é dado por
Substituindo as próximas reações de apoios teremos que
Agora que já temos as reações de apoio, vamos ao equilíbrio dos nós.
Passo 2
Agora vemos que na sequência do nosso passo a passo devemos começar resolvendo os nós que possuem apenas 2 barras, e que no nosso problema são exatamente os nós que foram pedidos para a solução no enunciado. Sabemos que a primeira coisa que devemos fazer é cortar o pórtico no nó que iremos calcular e levarmos até esse nó todos os esforços que foram descartados com o corte do pórtico, começando pelo nó B teremos
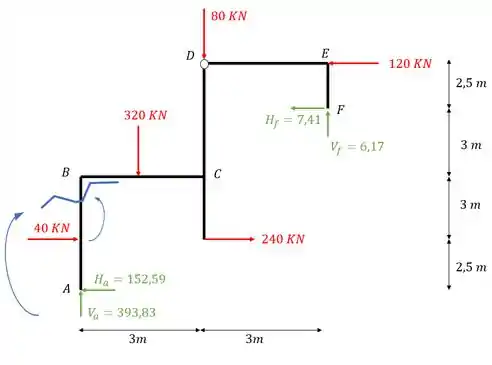
Perceba que o corte que faremos irá dispensar as reações do apoio A, e o carregamento de 40KN, logo, devemos levar para o nó tudo aquilo que seria perdido tanto com relação aos apoios, quanto com relação aos carregamentos, sendo assim o nosso nó B ficaria
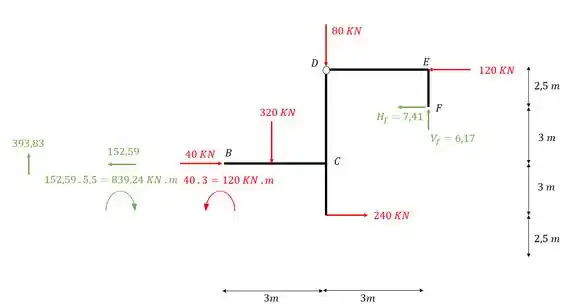
Juntando os carregamentos com mesmo direcionamento, teremos que
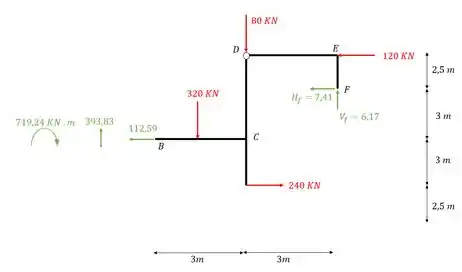
Equilibrando o nó B teremos que
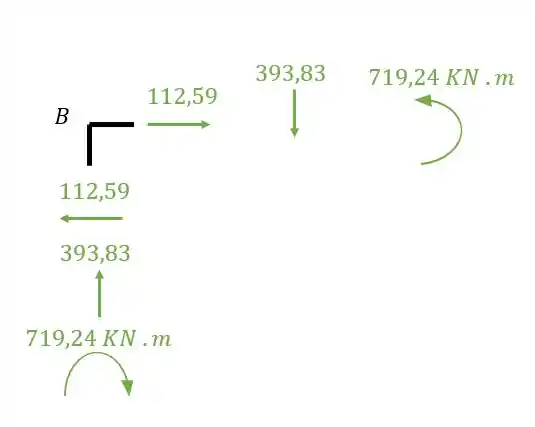
Vemos que na barra AB a carga de 112,59 é cortante, mas na barra BC ela é normal, e ainda sim o nosso nó B está equilibrado. E quanto ao momento fletor o momento vai crescendo até 719,24 na barra AB e na barra BC será crescente a partir de 719,24 por todo o comprimento da barra.
Feito o equilíbrio do nó B vamos ao nó E.
Passo 3
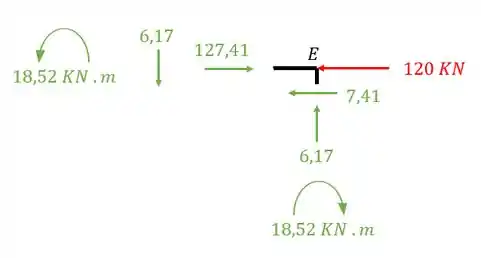
Sabemos que a primeira coisa que devemos fazer é cortar o pórtico no nó que iremos calcular e levarmos até esse nó todos os esforços que foram descartados com o corte do pórtico, fazendo isso para o nó E teremos
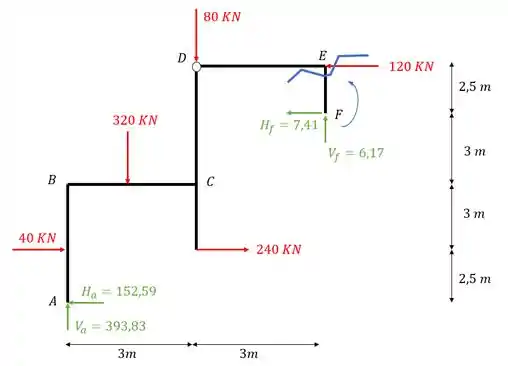
Perceba que o corte que faremos irá dispensar as reações de apoio em F, logo, devemos levar para o nó E tudo aquilo que seria perdido quando retirássemos essa barra, com isso teremos
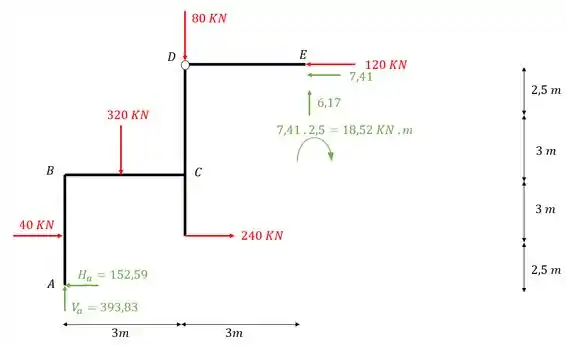
Equilibrando o nó E teremos que
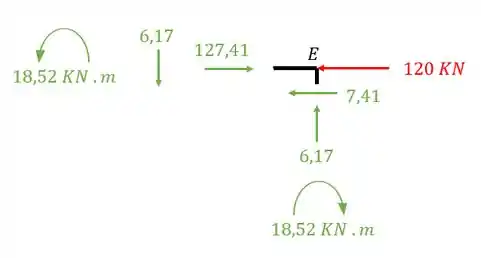
Vemos que na barra EF a carga de 6,17 é normal de compressão, mas na barra ED ela é cortante, e ainda sim o nosso nó E está equilibrado. E quanto ao momento fletor o momento cresce até 18,52 na barra EF e na barra ED ele começa com 18,52 e decresce até zero no nó. E quanto ao esforço normal, vemos que na barra ED haverá um esforço normal devido ao carregamento de 120 KN mais a carga de 7,41 que é cortante na barra EF. Dessa forma fizemos também o equilíbrio do nó E.
Resposta
Nó B (barras AB e BC)
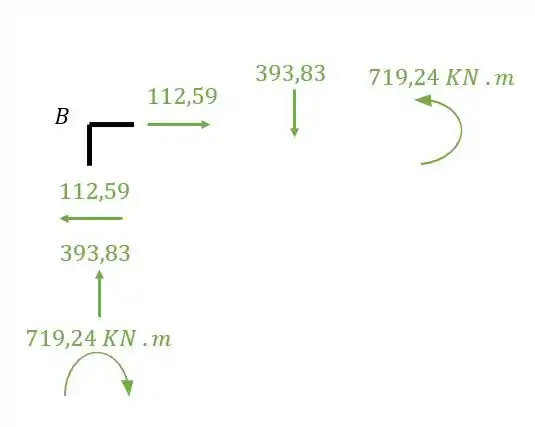
Nó E (barras EF e ED)