Calcule as reações de apoio do pórtico simples mostrado.
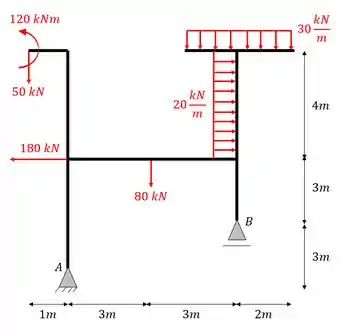
Passo 1
Para resolvermos qualquer exercício de pórticos simples, precisamos seguir uma sequência de passos que irá nos ajudar na solução desse tipo de problema, e a sequência é a seguinte.
- A primeira coisa que devemos fazer é o cálculo das reações de apoio, pois assim conseguiremos calcular qualquer nó sem que haja nenhum problema.
- a segunda coisa é seguir a seguinte sequência de nós a serem resolvidos:
Nós com 2 barras
Nós com 3 barras
Nós com 4 barras
...
- A terceira coisa que devemos fazer é calcular o valor dos momentos fletores, cortantes e normais em todos as barras que chegarem ou saírem de algum nó
- O quarto e último passo consiste em desenhar os diagramas do pórtico quando esse for pedido.
Agora que já sabemos qual sequência de passos devemos seguir, vamos aplicar esse conhecimento ao nosso problema.
Passo 2
Como vimos, a primeira coisa que devemos fazer é determinar as reações de apoio, para isso, primeiro iremos trocar os apoios por vetores reações de apoio, como indica a figura abaixo.
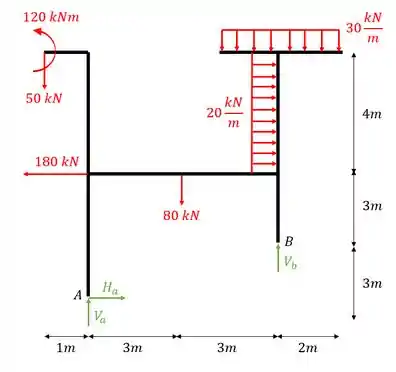
Agora que já temos os vetores e medidas, vamos fazer o equilíbrio de equações
E assim resolvemos o nosso problema, vamos para o próximo.