Ciclo de Rankine
Produzido por Rafael Cardoso BrandãoTeoria
Fala aí! Bora bater um papo sobre o Ciclo Rankine?!
Como Funciona o Ciclo de Rankine?
O ciclo de Rankine é o ciclo termodinâmico ideal que transforma calor em trabalho. Ele utiliza água como fluido de trabalho e gera energia ao mudar o estado da água, de vapor para líquido e vice-versa!
-Mas como?! 😖
Se liga nesse esqueminha:
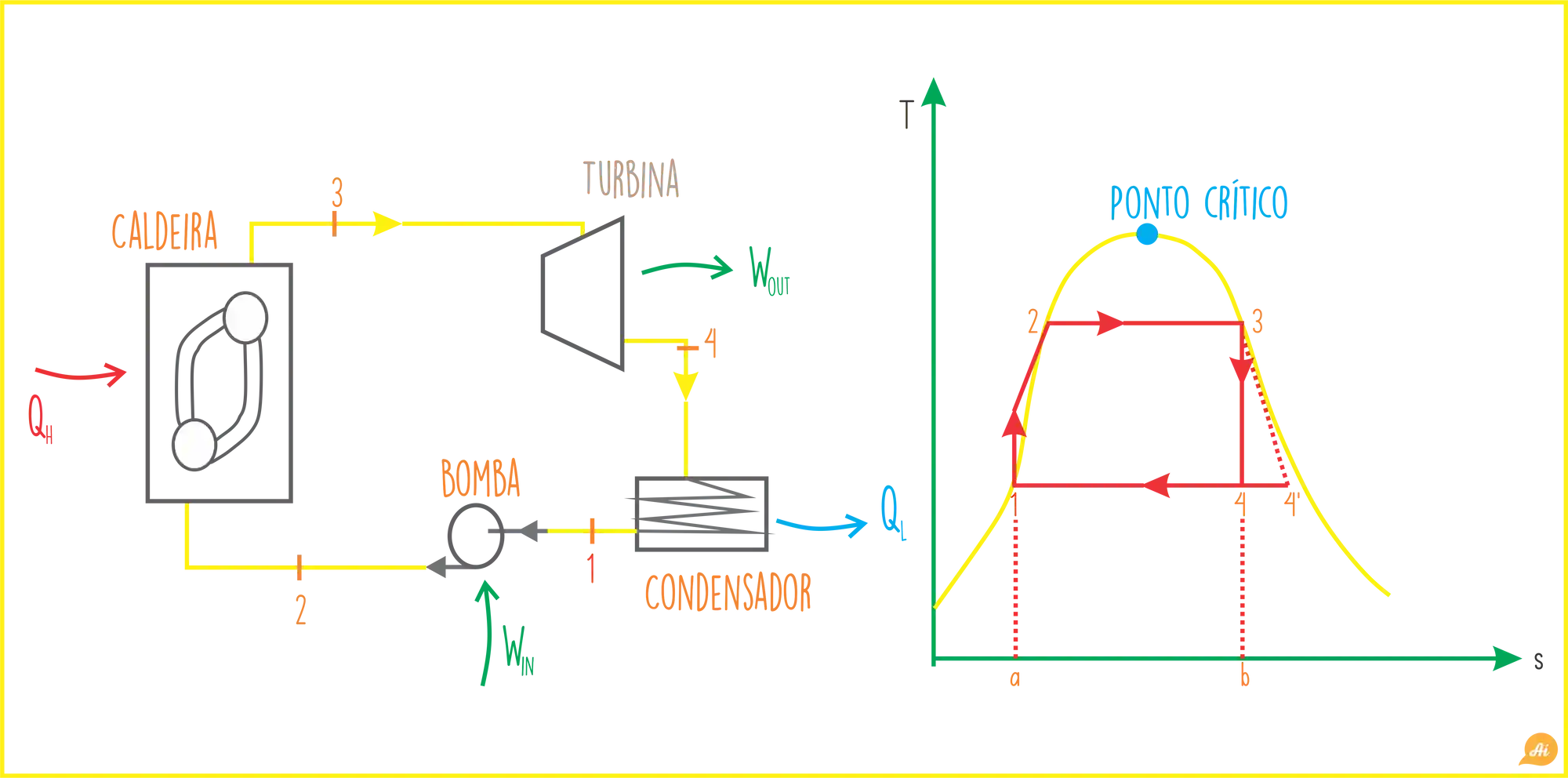
Antes de você ficar assustado com esse monte de equipamento, bora dar uma olhada na função de cada um dentro do ciclo!
BOMBA
O líquido condensado que sai do condensador, no final do ciclo, é bombeado até a caldeira pra recomeçar o ciclo! Nessa etapa a gente precisa fornecer energia pra bomba funcionar
CALDEIRA
Na caldeira o fluido de trabalho é aquecido até a saturação e evapora, ali mesmo. Esse vapor vai ser a estrela do nosso ciclo, você vai ver!
TURBINA
Se o vapor é a estrela do nosso ciclo, a turbina é o palco! O vapor passa pelas pás da turbina gerando trabalho
CONDENSADOR
Agora que o fluido de trabalho já fez o trabalho dele ( 🤣🤣🤣) precisamos prepara-lo pra reiniciar o ciclo! No condensado ocorre a transferência de calor do fluido de trabalho para a água de resfriamento. Depois disso o fluido passa pela bomba e tudo começa de novo!
📢 Clique para saber mais:
Etapas do Ciclo de Rankine
Agora sim, vamos entender o Ciclo Rankine do ponto de vista termodinâmico, que é o mais importante! Bora?
1 – 2: Processo adiabático reversível
Essa etapa ocorre na bomba, o fluido é bombeado e portanto sua temperatura aumenta ligeiramente. Além disso, não há troca de calor e, por ser reversível, não há nenhuma forma de atrito. Mas aqui existe um trabalho externo entrando no sistema o
Você também pode conferir esse conteúdo em vídeo! 👇
2 – 3: Processo Isobárico de Fornecimento de calor
Esse processo ocorre na caldeira, ou evaporador. Neste processo é interessante que a pressão da caldeira seja superior à pressão atmosférica, para atuar tipo uma panela de pressão, com temperaturas bem elevadas por causa da alta pressão.
3 – 4: Expansão Adiabática Reversível
Essa etapa ocorre na turbina e ele é o oposto do processo 1 – 2. Aqui o fluido perde energia (calor e velocidade) ao girar as pás da turbina, o que gerará trabalho
4 – 1: Processo Isobárico de Retirada de calor
Esse processo ocorre no no condensador, diferente do processo 2-3 não é necessário altas pressões!
O diagrama T x s fica da seguinte forma:
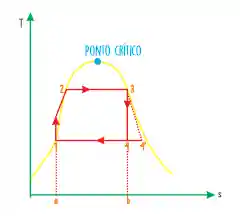
É bem legal perceber mais duas coisas sobre o ciclo de Rankine:
- O ponto
pode ser um estado de vapor saturado ou vapor superaquecido, isso vai depender do problema. - O caminho 3 – 4 é um processo adiabático reversível (ou isentrópico) enquanto o caminho 3 – 4’ é um processo adiabático irreversível (não é isentrópico) este processo ocorre quando há algum tipo de atrito, o processo não é perfeito. Pode-se ver isso pela inclinação da reta, quando ela for vertical a entropia se conserva e é igual a b, caso contrário a entropia não se conserva (e aumenta!).
Eficiência do Ciclo de Rankine
A eficiência é a razão entre a energia que a gente conseguiu produzir e a energia que deveria ser produzida. Como se trata de um ciclo de potência então que quero potência
Aplicando a primeira lei da termodinâmica:
Ciclo de Rankine com Reaquecimento
No ciclo de rankine com reaquecimento é possível aumentar a eficiência, ele funciona da seguinte forma:
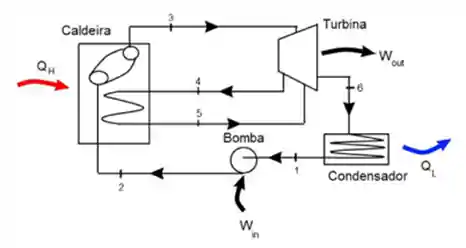
A única diferença entre o ciclo rankine com reaquecimento e o ciclo rankine normal é que depois do fluido passar na turbina ele passa pela caldeira novamente, retorna à turbina e finalmente segue seu caminho para o condensador. Isso é feito porque o fluido sai da turbina com muita energia ainda, mas como uma mistura de vapor e líquido, por isso passa na caldeira para retornar ao estado de vapor e volta à turbina. Esse processo pode acontecer mais de uma vez e diz-se um ciclo de reaquecimento em mais de um estágio.
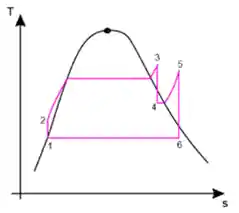
No ciclo de rankine com reaquecimento o vapor passa mais de uma vez na turbina, Isso faz com que a potência aumenta sem termos que injetar mais calor, ou seja, maior eficiência, que pode ser calculada por:
Ciclo de Rankine com Regeneração
Outra forma de poder reaproveitar uma energia que seria desperdiçada é aquecer o fluido antes de entrar na caldeira, utilizando o calor que seria perdido pela turbina para o ambiente. Além disso o ciclo regenerativo conta, também, com um aquecedor de água como mostrado no esquema e diagrama a seguir:
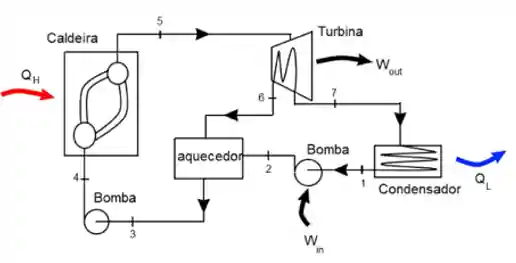
Etapas do Ciclo de Rankine com Regeneração
Agora vamos ver como funciona o ciclo de rankine com regeneração na prática! Ele tem as seguintes etapas:
- Primeiramente o fluido passa por um aquecedor, processo 2 – 3, que aumenta a temperatura de fornecimento de calor que ocorrerá na caldeira, como vimos isso aumenta a eficiência do ciclo e utiliza a energia térmica da própria turbina.
- Depois o líquido tem que passar por uma nova bomba, processo 3 – 4, para elevar a pressão e entrar na caldeira.
- Na turbina ocorre uma separação e parte da massa vai para o caminho normal do condensador, processo 7 – 1, e outra para o aquecedor, processo 6 – 3, para aquecer o fluido do processo 2 – 3, de forma a utilizar o restinho do calor que essa água ainda tinha para aquecer a outra parte da água que está um pouco mais gelada.
O diagrama T×s do ciclo de rankine com regeneração ficará da seguinte forma:
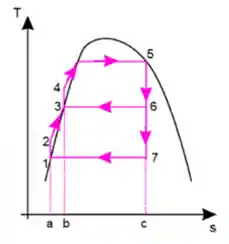
Agora vamos praticar com exercícios?!
Eficiência do Ciclo de Rankine
Ciclo de Rankine com Reaquecimento
Ciclo de Rankine com Regeneração
Exercícios Resolvidos
Exercício Resolvido #1
Elaboração própria
Identifique no diagrama abaixo os processos adiabáticos e os processos isobáricos, de um ciclo Rankine. Além disso, explique porque dentro da curva de saturação temos processos isotérmicos.
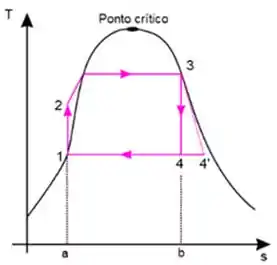
Passo 1
Os processos adiabáticos são os processos de 1 – 2; 3 – 4. Além disso esses processos também são reversíveis e portanto isentrópicos (perceba que eles são verticais).
Um ciclo de Rankine pode não ser reversível (na realidade de fato não será) o que está representado no processo 3 – 4’, este processo também é adiabático, porém, não é reversível e, portanto, não é isentrópico.
Assim, um ciclo reversível tem a cara de 1 – 2 – 3 – 4 – 1.
E um ciclo irreversível tem a cara de 1 – 2 – 3 – 4’ – 1.
Passo 2
Já as isobáricas são os processos 2 – 3 e 4 – 1.
Passo 3
Perceba que quando uma isobárica se encontra dentro da curva de saturação (aquele sino preto) estamos falando de uma troca de fase, do líquido para o vapor no processo 2 – 3 e do vapor para o líquido no processo 4 – 1.
Quando há troca de fase a pressão e a temperatura são dependentes, logo, num processo isobárico (a pressão constante) a temperatura também se manterá constante.
Resposta
Ei, a resposta está no passo a passo :)
Exercício Resolvido #2
Elaboração própria
Explique as vantagens de se ter um ciclo Rankine com superaquecimento. Explique também a diferença entre o ciclo Rankine padrão e um ciclo com reaquecimento e regeneração.
Passo 1
O ciclo Rankine com superaquecimento traz duas vantagens. A primeira é o fato do vapor superaquecido possuir uma temperatura mais elevada do que o vapor saturado e a eficiência do ciclo Rankine aumenta quando a temperatura de recebimento de calor também aumenta.
A segunda vantagem está no fato de, ao condensar, o título é maior no caso com superaquecimento. Assim há menos líquido na saída da turbina, melhorando sua eficiência.
Passo 2
Um ciclo rankine com reaquecimento tem função parecida do que o superaquecimento. Após passar pelos estágios de alta pressão da turbina o fluido retorna à caldeira para voltar ao estado de vapor superaquecido.
Apesar de haver um ligeiro aumento na eficiência, o mais importante aqui é diminuir o teor de umidade nos estágios de baixa pressão da turbina.
obs: Como a turbina é um equipamento que gira muito rapidamente até a menor gota d’água pode trazer problemas para seu funcionamento.
Passo 3
Já o ciclo Rankine com regeneração circula o fluido em volta da turbina, e passa por um aquecedor, afim de reutilizar o calor que antes seria desperdiçado na atmosfera. O fluido é, então, direcionado à caldeira e o ciclo continua.
Como o fluido já vai para a caldeira previamente aquecido o calor é menor. Desta forma, a eficiência do ciclo todo aumenta.
Aqui vale outra observação. Se o ciclo conseguisse reutilizar todo o calor rejeitado pela turbina e não utilizar o aquecedor, então o ciclo de Rankine se torna ideal e seu rendimento igual ao da máquina de Carnot.
Resposta
Ei, a resposta está no passo a passo :)
Exercício Resolvido #3
Elaboração própria
Num ciclo Rankine como mostrado na figura abaixo. Ache um jeito de calcular a eficiência do ciclo utilizando apenas as entalpias dos estados.
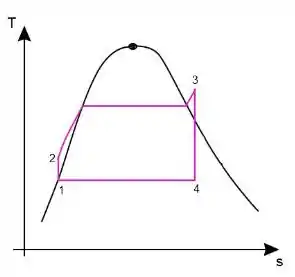
Passo 1
Primeiramente a eficiência de um ciclo rankine é dada por
onde é o trabalho gerado pela turbina, o trabalho consumido pela bomba e o calor que entra no ciclo.
Passo 2
É muito importante perceber que o calor trocado nesse ciclo é sempre por meio de um processo isobárico, sendo assim o calor é igual a variação da entalpia.
Passo 3
Além disso os trabalhos isentrópicos também são iguais a variação da entalpia, porém fica atento que aqui a ordem da subtração das entalpias se inverte. Isso é explicado porque estamos utilizando a notação de que o trabalho positivo sai do sistema enquanto o calor positivo entra no sistema
obs: Aqui vale lembrar que os trabalhos são de fluxo, em regime permanente, ou seja há variação da pressão porém o volume específico permanece constante. Por isso podem também ser calculados como
Passo 4
Agora vamos substituir a relação entre os trabalhos e calores com as entalpias.
Aqui utilizamos o módulo porque a equação já possui um sinal negativo simbolizando que este trabalho é injetado no ciclo.
Resposta
Exercício Resolvido #4
Gordon Van Wylen, Richard Sonntag e Claus Borgnakke, Fundamentos da termodinâmica clássica, Tradução da 4ª ed. americana. São Paulo: Edgard Blucher, 1995, pp.247 – Exemplo 9.1
Determine o rendimento de um ciclo de Rankine que utiliza água como fluido de trabalho e no qual a pressão no condensador é igual a 10 kPa e o fluido entra na bomba como líquido saturado a 10 kPa e . A pressão na caldeira é de 2 MPa. O vapor deixa a caldeira como vapor saturado.
Dados: Entalpia do vapor saturado a 2 MPa é 2799,5 kJ/kg; Entalpia do líquido saturado a 10kPa é 193,8 kJ/kg.
Entropia do estado de vapor saturado e
Entalpias para o estado de vapor saturado ,
Passo 1
Um ciclo de geração de potência é definido como
Portanto, precisamos achar o trabalho da bomba, da turbina e a quantidade de calor fornecida ao ciclo.
Passo 2
Vamos calcular o trabalho fornecido à bomba. Nesse caso estamos falando de um trabalho de fluxo, onde o volume específico permanece constante e a pressão varia, portanto
Como o fluido entra na bomba como líquido saturado a 10 kPa e . Assim
Passo 3
Agora vamos calcular , que é igual a diferença de entalpia entre os estados de vapor saturado a 2 MPa e líquido saturado a 10kPa. Portanto, temos
Passo 4
Agora basta calcular o trabalho gerado pela turbina que também é igual a diferença das entalpias. Mas nesse caso não temos o estado 4 definido. Como vamos descobrir esse estado?
A resposta é simples. O processo 3 – 4 não é uma isentrópica? E termina com pressão de 10 kPa? Sim! Então basta fazer a seguinte conta
Ou
Como temos a entropia do estado 3 também temos do estado 4 e e são dados.
Vamos utilizar a primeira onde e
Agora temos a pressão, a temperatura e o título, portanto, temos um estado termodinâmico definido. Agora é só usar o dado da entalpia e ver que , e fazer o processo inverso.
Logo o trabalho gerado pela turbina é igual a
Passo 5
Agora basta substituir e achar o rendimento
Resposta
Exercício Resolvido #5
Escola politécnica da cidade de São Paulo, Ciclo de motores a vapor, p. 16
Calcular o rendimento térmico e o título na saída do ciclo Rankine, que opera entre 4 MPa e 7,5kPa, sem superaquecimento.
Passo 1
Vamos lá! O desenho abaixo mostra o diagrama sem superaquecimento.
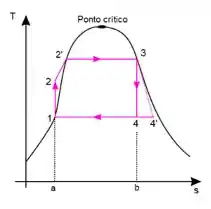
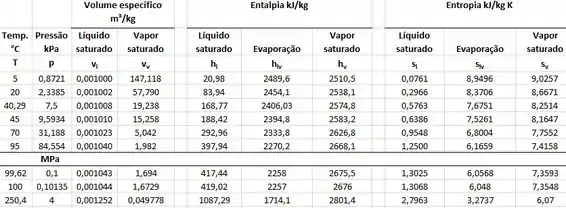
Para resolver esse problema vamos ter que dar uma olhada nas tabelas de da água, assim, vamos achar o título e as entalpias de cada estado termodinâmico e, finalmente, calcular a eficiência.
Passo 2
A eficiência é dada por
O trabalho da bomba é um trabalho de fluxo, ou seja, há variação da pressão enquanto o volume específico se mantém constante, portanto é definido como
Pela tabela de saturação, o líquido saturado a pressão de 7,5 kPa tem
Então o trabalho consumido na bomba é de
Passo 3
Como o trabalho também pode ser calculado como a diferença de entalpias, e pela tabela a entalpia de um líquido saturado a pressão de 7,5 kPa é , então
Observe que o sinal negativo foi colocado porque a bomba recebe trabalho, ao invés de gerar.
Agora já temos a entalpia dos estados 1 e 2, vamos calcular a do estado 3.
Passo 4
O estado 3 é um estado de vapor saturado com pressão de 4 MPa. Com isso podemos saber, pela tabela, que neste estado temos:
Passo 5
Agora vamos descobrir a entalpia do estado 4. Neste estado estaremos trabalhando novamente com a pressão de 7,5 kPa e temperatura de 40,29°C mas presta atenção, aqui temos uma mistura de líquido e vapor, então esse estado é diferente do 1.
Com isso precisamos saber o título deste estado, que achamos por meio da entropia. Como o processo 3 – 4 é isentrópico, então a entropia de 4 é igual a de 3.
Fazendo um processo semelhante para achar a entalpia
Passo 6
Agora podemos achar o rendimento para o ciclo sem superaquecimento
Como podemos colocar todos esses valores com diferenças de entalpias, temos
Resposta
Exercício Resolvido #6
Escola politécnica da cidade de São Paulo, Ciclo de motores a vapor, p. 16
Calcular o rendimento térmico e o título na saída do ciclo Rankine, que opera entre 4 MPa e 7,5kPa, com superaquecimento de 250°C.
Passo 1
A diferença básica entre os dois ciclos é que no sem superaquecimento o vapor entra como vapor saturado na turbina, ou seja, esse ponto está exatamente sobre o “sino”. Já no ciclo com superaquecimento o vapor entra na turbina como vapor superaquecido, ou seja, este ponto está acima do “sino”. O desenho abaixo mostra o diagrama com superaquecimento.
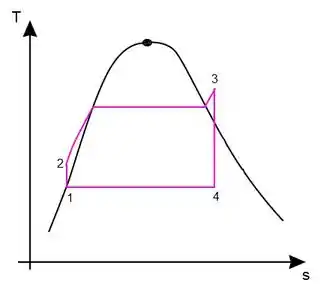
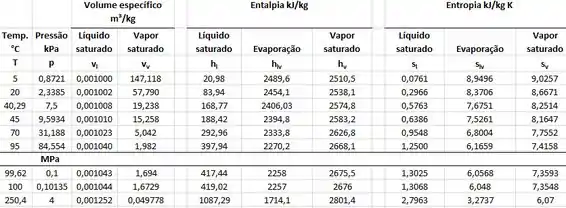
Para resolver esse problema vamos ter que dar uma olhada nas tabelas de saturação e de vapor superaquecido da água, assim, vamos achar o título e as entalpias de cada estado termodinâmico e, finalmente, calcular a eficiência.
Passo 2
A eficiência é dada por
O trabalho da bomba é um trabalho de fluxo, ou seja, há variação da pressão enquanto o volume específico se mantém constante, portanto é definido como
Pela tabela de saturação, o líquido saturado a pressão de 7,5 kPa tem
Então o trabalho consumido na bomba é de
Passo 3
Como o trabalho também pode ser calculado como a diferença de entalpias, e pela tabela a entalpia de um líquido saturado a pressão de 7,5 kPa é , então
Observe que o sinal negativo foi colocado porque a bomba recebe trabalho, ao invés de gerar.
Agora já temos a entalpia dos estados 1 e 2, vamos calcular a do estado 3.
Passo 4
O estado 3 é um estado de vapor superaquecido com pressão de 4 MPa. Como sabemos a pressão, temos de saber também a temperatura, como o enunciado nos forneceu que o superaquecimento é de 250°C então
Esse 250,40 que somamos é a temperatura de saturação na pressão de 4Mpa. Por isso que T3 vai ser soma da temperatura de saturação com a temperatura de aquecimento.
Com os dados fornecidos neste estado temos:
Passo 5
Agora vamos descobrir a entalpia do estado 4. Neste estado estaremos trabalhando novamente com a pressão de 7,5 kPa e temperatura de 40,29°C mas presta atenção, aqui temos uma mistura de líquido e vapor, então esse estado é diferente do 1.
Com isso precisamos saber o título deste estado, que achamos por meio da entropia. Como o processo 3 – 4 é isentrópico, então a entropia de 4 é igual a de 3.
Fazendo um processo semelhante para achar a entalpia
Passo 6
Agora podemos achar o rendimento para o ciclo sem superaquecimento
Como podemos colocar todos esses valores com diferenças de entalpias, temos
Resposta
Exercício Resolvido #7
Gordon Van Wylen, Richard Sonntag e Claus Borgnakke, Fundamentos da termodinâmica clássica, Tradução da 4ª ed. americana. São Paulo: Edgard Blucher, 1995, pp.291 – Exercício 9.3
Uma central de potência a vapor, operando num ciclo de Rankine, apresenta pressão máxima igual a 5 MPa e mínima de 15 kPa. Sabendo que o valor mínimo aceitável para o título do vapor na seção de saída da turbina é de 95% e que a potência gerada na turbina é igual a 7,5MW, determine qual é a temperatura de descarga da caldeira e a vazão em massa no ciclo.
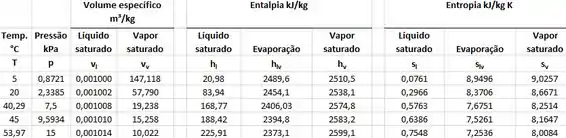
Dado: Para o vapor superaquecido a 700°C têm-se uma entropia igual a 7,5122 e para a temperatura de 800°C a entropia é igual a 7,7440.
Passo 1
Para começar esse problema, e qualquer outro desse tópico, temos de achar as propriedades de algum estado termodinâmico. Lembrando que um estado termodinâmico é definido por duas propriedades independentes (como a pressão e a temperaura) e, se for o caso de uma mistura de fases, o título também deve ser considerado já que na mudança de fase a pressão e temperatura são dependentes.
O meio mais fácil de achar esse estado é a saída da turbina que é onde ocorre a pressão mínima de 15 kPa e o título de 95%, essas duas propriedades já bastam e o estado está definido. Vamos ter apenas que olhar na tabela e fazer aquelas operações para achar outras propriedades importantes como a entropia e a entalpia.
Passo 2
Calculando a entalpia e entropia do estado 4 (saída da turbina). Ao olhar a tabela da água saturada a 15 kPa encontramos que
Como sabemos que o título é igual a 95% podemos calcular a entalpia e a entropia desse estado da forma:
Passo 3
Agora vamos achar a temperatura de descarga da caldeira, que é a mesma de entrada na turbina. Vamos fazer isso lembrando que o processo na turbina é isentrópico ou seja , como sabemos também que a pressão é de 5 MPa basta ir novamente na tabela. Quando olhamos na tabela de vapor d’água superaquecido, na parte referente à pressão de 5 MPa, vemos que essa entropia de não é encontrada diretamente, porém, está entre os valores de 7,5122 e 7,7440 que representam, respectivamente, as temperaturas 700°C e 800°C.
Então agora é só fazer uma interpolação linear (aquela lá de quando estudamos transformação de celsius para fahrenheit) para achar a temperatura aproximada:
Passo 4
Agora vamos achar a vazão mássica, faremos isso por meio da potência da turbina que foi dada na questão:
Agora nos deparamos com uma situação parecida com a do passo anterior, pois sabemos o estado 3 mas a tabela não fornece o valor exato. Então, vamos ter que fazer novamente uma interpolação.
Resposta
Exercício Resolvido #8
Gordon Van Wylen, Richard Sonntag e Claus Borgnakke, Fundamentos da termodinâmica clássica, Tradução da 4ª ed. americana. São Paulo: Edgard Blucher, 1995, pp.250 – Exemplo 9.2
Num ciclo Rankine, o vapor d’água deixa a caldeira e entra na turbina a 4 MPa e 400°C. A pressão no condensador é de 10 kPa. Determine o rendimento do ciclo.
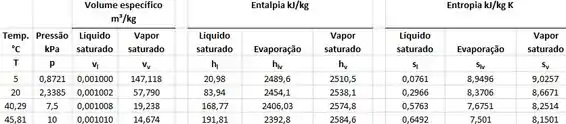
Dado: Água a 4MPa e temperatura de 400°C tem e .
Passo 1
A eficiência de um ciclo de geração de potência é definida coma
Portanto, precisamos achar o trabalho da bomba, da turbina e a quantidade de calor fornecida ao ciclo.
Passo 2
Vamos calcular o trabalho fornecido à bomba. Nesse caso estamos falando de um trabalho de fluxo, onde o volume específico permanece constante e a pressão varia, portanto
Como o fluido entra na bomba como líquido saturado a 10 kPa podemos ver, pela tabela, que . Assim
Além disso podemos lembrar que e assim acharmos a entalpia do estado 2:
Pela tabela a entalpia do estado 1 vale 191,8 kJ/kg, logo
Passo 3
Analisando a turbina vamos ter que, pela primeira lei e, pela segunda lei, teremos que . Pelo dado do problema também conseguimos ver que no estado de pressão igual a 4MPa e temperatura de 400°C a água tem e .
Para a entalpia vamos utilizar e obtemos:
Portanto o trabalho da turbina será de
e o trabalho líquido será
Passo 4
Agora vamos calcular , que é igual a diferença de entalpia entre os estados de vapor saturado a 4 MPa e líquido saturado a 10kPa. Portanto, segundo a tabela, temos
Passo 5
Agora basta substituir e achar o rendimento
Resposta
Exercício Resolvido #9
Gordon Van Wylen, Richard Sonntag e Claus Borgnakke, Fundamentos da termodinâmica clássica, Tradução da 4ª ed. americana. São Paulo: Edgard Blucher, 1995, pp.259 – Exemplo 9.5
Uma central térmica a vapor opera segundo um ciclo com as seguintes pressões e temperaturas:
- Entrada da caldeira: e
- Saída da caldeira: e
- Entrada da turbina e
- Entrada na bomba: e
- Saída da bomba:
Sabendo que a eficiência da turbina é de 86% e que a eficiência da bomba é 80%, determine o rendimento térmico deste ciclo.
Dados: Vapor d’água a 380°C e 3,8MPa e ;
As entalpias para o caso isentrópico seriam e
Passo 1
A eficiência de um ciclo de geração de potência é definida coma
Portanto, precisamos achar o trabalho da bomba, da turbina e a quantidade de calor fornecida ao ciclo.
Passo 2
Vamos calcular o trabalho gerado pela turbina. Faremos isso utilizando a relação que vêm da 1ª lei e sabemos também, pela 2ª lei que onde é a entropia do estado 6 caso se trata-se de uma adiabática reversível (isentrópica).
Assim a eficiência da turbina pode ser descrita como:
Os dados do vapor d’água fornecem e Assim
Agora, com o título, conseguimos achar
Portanto o trabalho da turbina é
Passo 3
Nesse passo iremos fazer a mesma coisa do passo 2, mas para a bomba agora, por isso vamos ter e .
Como podemos utilizar a equação para trabalho de fluxo
Portanto o trabalho da bomba é
Lembrando que o valor de também foi retirado da tabela.
Passo 4
Agora vamos calcular , que é igual a diferença de entalpia entre 4 e 3
Passo 5
Agora basta substituir e achar o rendimento