Enunciado
Termodinâmica - Van Wylen- Ed: 6º - Capítulo 11.Problemas - Ex. 29
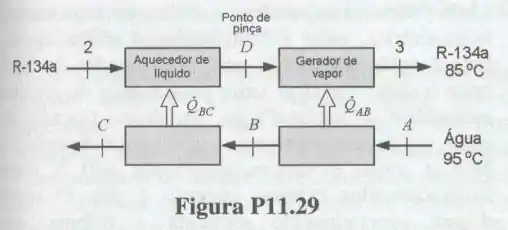
Considere o gerador de vapor descrito no Prob. 11.26 onde a água quente aquece o R-134a até que ele se transforme em vapor saturado. Admita que o gerador de vapor é um trocador de calor contra-corrente. A temperatura da água quente deve ser igual ou maior do que a temperatura do R-134a em qualquer posição do trocador de calor. O ponto que apresenta a menor diferença entre as temperaturas da água e do fluido de trabalho é denominado ponto de pinça (veja a Fig. P11.29). Determine a máxima potência produzida nesse ciclo quando a vazão e a temperatura de água quente disponível forem iguais a e .
Passo 1
Bora resolver esse problema juntos!
Começamos o problema aplicando a equação de energia para a primeira seção :
Agora, na seção :
Todas as propriedades desse exercício vão ser obtidas pelas Tabelas B.1.1 e B.5.1, para a água e para o R-134a, sob suas respectivas temperaturas:
Sendo:
Temos:
Assim, jogando na segunda equação:
Passo 2
Para termos certeza de que a temperatura de ebulição é o fator restritivo, calculamos da equação de energia para a seção restante:
Tomando como aproximadamente
Aplicando na segunda parte da equação:
Pela Tabela B.1.1, temos:
Passo 3
Para determinarmos a máxima potência produzida nesse ciclo, devemos analisar os integrantes do ciclo que produzem trabalho separadamente.
Aqui, devemos pegar algumas informações do Prob. 11.26.
Começamos pela bomba.
Aqui temos um processo isentrópico e incompressível, assim podemos calcular seu trabalho como:
Passo 4
Passando para a turbina, temos novamente um processo isentrópico, então:
Calculando :
Aplicando a equação de energia:
Passo 5
Por fim, calculando a máxima potência produzida nesse ciclo:
Assim:
Ufa! Acabamos!
Até a próxima questão!