Ciclo de Potência
Produzido por Rafael Cardoso BrandãoTeoria
Preparado para aprender sobre ciclo de potência? Então vem comigo
Um ciclo de potência nada mais é que um conjunto de processos que tem por objetivo final gerar trabalho.
A gente pode não saber, mas os ciclos de potência estão presentes no nosso dia a dia. Motores em geral possuem em seu interior ciclo de potência.
De maneira resumida, o que um ciclo de potência faz é pegar calor de uma fonte quente (chamamos esse calor de calor quente -
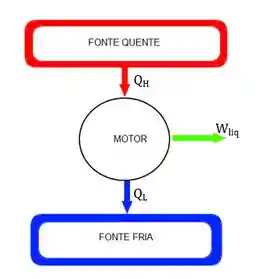
E como a energia tem que ser sempre conservada, temos que todo o calor quente é transformado em trabalho líquido e calor frio:
É muito importante perceber que um ciclo de potência nunca terá eficiência de
E falando nisso, a eficiência, representada por
Por exemplo, se um ciclo de potêcia utiliza
E a partir do balanço de energia, conseguimos calcular a quantidade de calor frio "jogado para fora":
Mas, o interior do ciclo de potência não é tão simples assim!

Na verdade, para o calor ser transformado em trabalho precisa de um conjunto de equipamentos no interior do ciclo:
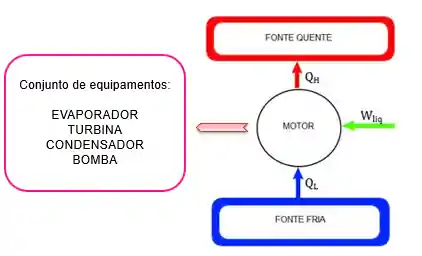
Nos próximos tópicos você vai entender melhor sobre esses equipamentos e o interior do motor em um ciclo de potência. A notícia boa é que temos as leis e as relações termodinâmicas para nos ajudar 🎉
Por enquanto é isso que você precisa saber, vamos para os exercícios praticar e depois avançar no conteúdo 😉
Exercícios Resolvidos
Exercício Resolvido #1
Formulação própria
Um jovem estudante de termodinâmica foi pegar sua preciosa cerveja na geladeira e reparou que, pelo fato do dia estar mais frio do que o normal, sua cerveja congelou. Explique porque a temperatura da geladeira diminui quando o ambiente externo se torna mais frio.
Passo 1
A geladeira é um refrigerador que utiliza um pequeno motor para fazer o fluxo de calor se inverter, ou seja, fluir do reservatório mais frio (interior da geladeira) para o mais quente (ambiente).
Isso tudo acontece por meio do fluido de trabalho (esse fluido que transporta o calor). Normalmente esse fluido irá roubar calor de dentro da geladeira e, ao entrar em contato com o ambiente externo, libera esse calor para o ambiente.
O fluido consegue ceder calor ao ambiente por estar mais quente do que esse, e roubar calor da geladeira por estar mais frio do que essa. Observe a figura abaixo e veja como fluido rouba calor da geladeira quando está frio e cede calor ao ambiente quando está quente.
É interessante também perceber que quando o fluido rouba calor ele aquece e quando cede calor ele resfria.
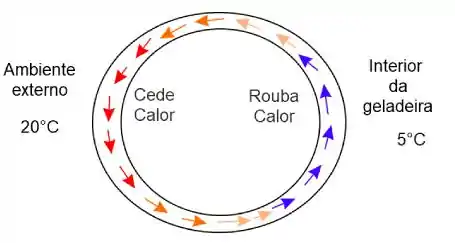
Então quando a temperatura ambiente cai a diferença de temperatura entre o fluido e o ambiente se torna maior, aumentando assim a troca de calor. Como estamos falando de calor trocado com o reservatório frio então é o que aumenta.
Como o consumo de energia da geladeira não muda permanece constante e utilizando a primeira lei aplicada aos ciclos:
Vamos perceber que também deve aumentar para que permaneça constante. Sendo assim o fluido irá roubar mais calor () da geladeira deixando-a mais fria do que o normal.
Resposta
Ei, a resposta está no passo a passo :)
Exercício Resolvido #2
Formulação própria
Num laboratório de termodinâmica o professor mostrou que um mesmo ciclo pode ser utilizado como máquina térmica, refrigerador ou bomba de calor. Sabendo que esse ciclo opera sempre com o calor da fonte fria de 300J e calor da fonte quente de 500J. Qual a eficiência deste ciclo para cada caso de utilização?
Passo 1
Primeiro vamos lembrar que num ciclo completo a energia interna não varia. Para o caso de uma máquina térmica temos que
Ou para o caso de refrigeradores e bombas de calor temos
Portanto, independentemente de como esse ciclo será utilizado o trabalho cedido ao ciclo, ou realizado por ele, sempre será igual a 200J.
Passo 2
Agora vamos calcular a eficiência para cada caso lembrando que eficiência é uma razão entre o que eu quero sobre o que eu gasto.
Passo 3
Putz!! Deu ruim! Deu uma eficiência maior do que 100% para e , e agora? Tranquilo, jovem gafanhoto, isso acontece mesmo. Para o caso de refrigeradores e bombas de calor a eficiência pode ser maior do que 100% mesmo. Isso só não pode acontecer para os motores ().
Se quiser ainda dar mais aquela conferidinha subtrai de ’ e vê se da 1!
Show de bola! Então provavelmente o resultado realmente está correto!
Resposta
Exercício Resolvido #3
Formulação própria
Num laboratório de termodinâmica o professor mostrou que um mesmo ciclo pode ser utilizado como máquina térmica, refrigerador ou bomba de calor. Sabendo que esse ciclo opera sempre com o calor da fonte fria de 300J e calor da fonte quente de 500J. Qual a eficiência deste ciclo para cada caso de utilização?
Passo 1
Primeiro vamos lembrar que num ciclo completo a energia interna não varia. Para o caso de uma máquina térmica temos que
Ou para o caso de refrigeradores e bombas de calor temos
Portanto, independentemente de como esse ciclo será utilizado o trabalho cedido ao ciclo, ou realizado por ele, sempre será igual a 200J.
Passo 2
Agora vamos calcular a eficiência para cada caso lembrando que eficiência é uma razão entre o que eu quero sobre o que eu gasto.
Passo 3
Putz!! Deu ruim! Deu uma eficiência maior do que 100% para e , e agora? Tranquilo, jovem gafanhoto, isso acontece mesmo. Para o caso de refrigeradores e bombas de calor a eficiência pode ser maior do que 100% mesmo. Isso só não pode acontecer para os motores ().
Se quiser ainda dar mais aquela conferidinha subtrai de ’ e vê se da 1!
Show de bola! Então provavelmente o resultado realmente está correto!
Resposta
Exercício Resolvido #4
Lista UNICAMP.
Um ciclo motor opera segundo o ciclo representado abaixo. Sabendo que a taxa dos calores trocados estão representados no sistema. Calcule a eficiência deste ciclo.
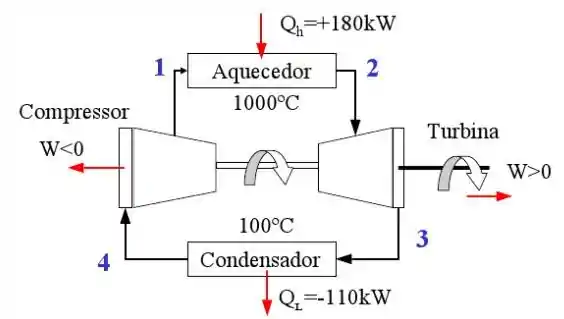
Passo 1
Como os dados fornecidos foram e vamos calcular o para achar a eficiência.
Pela primeira lei da termodinâmica. Aqui vale lembrar que estamos falando de potência ao invés de trabalho, portanto, estamos falando das taxas de calor trocada. Por isso a utilização do pequeno ponto acima dos termos.
Passo 2
Substituindo na equação da eficiência
Resposta
Exercício Resolvido #5
Formulação própria
Numa fábrica de sorvete deve-se manter a câmara fria a uma temperatura de -20°C. Para isso é necessário remover 200 kJ de calor por segundo da câmara. Sabendo que a fábrica dispõe de uma máquina térmica, que recebe 100 kJ de calor por segundo da fonte quente e possui eficiência de 80%, para fornecer energia à câmara fria. Qual a eficiência mínima da câmara fria para que essa operação possa ser realizada?
Passo 1
Vamos lembrar das eficiências do ciclo refrigerador e da máquina térmica, respectivamente:
Se temos de remover 200 kJ da câmara fria, então esse é o nosso do refrigerador. Como um manda trabalho para o outro, ambos são iguais. Por fim, o da máquina é o quanto de calor entra nessa máquina, sendo igual a 100 kJ, com eficiência de 80%.
Passo 2
Agora perceba que, com a equação da eficiência da máquina térmica, é possível achar o trabalho gerado.
Passo 3
Agora aplicamos esse trabalho achado no passo 2 na equação da eficiência do refrigerador.
Resposta
Exercício Resolvido #6
USP, Fundamentos de termodinâmica e ciclos de potência, prof. Dr. José R. Simões Moreira.
Uma bomba de calor é utilizada para atender às necessidades de aquecimento de uma casa, mantendo-a a 20 °C. Nos dias em que a temperatura externa cai para -2 °C, estima-se de uma perda de calor da casa a uma taxa de 80000 kJ/h. Se a bomba de calor nessas condições tiver um COP de 2,5, determine (a) a potência consumida pela bomba de calor e (b) a taxa com que o calor é removido do ar frio externo.
Passo 1
Neste problema estamos falando de uma bomba de calor que transfere calor do ambiente mais frio para o mais quente quando recebe trabalho externo. O problema pede a potência, que é esse trabalho externo () pelo tempo (, e a taxa de calor removido do ar frio externo (.
Outra coisa muito importante é o COP do inglês (Coefficient of performance), que é a eficiência da bomba de calor, que a gente chama de , dada por
Ou, em termos de potência e taxa de transferência de calor:
Passo 2
Se a casa perde 80000 kJ/h de calor, para permanecer na mesma temperatura ela tem que ganhar 80000 kJ/h de calor também. Com isso, e o coeficiente de rendimento de 2,5 podemos achar a potência da bomba de calor.
Para achar o resultado em Watts, basta transformar
Passo 3
Agora se temos tanto a potência quanto a taxa de calor quente transferido podemos achar o calor frio com facilidade, pela primeira lei
Aqui dividimos por 3600 para achar em kW, igual no passo 2.
Resposta
Exercício Resolvido #7
Formulação própria
Um ciclo termodinâmico funciona segundo o ciclo termodinâmico mostrado abaixo
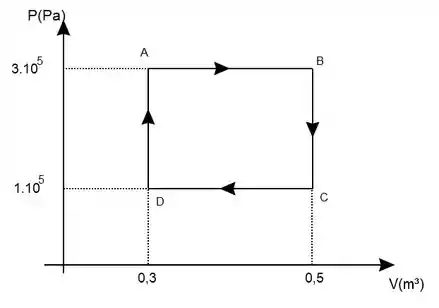
a) Este ciclo trata de um motor ou refrigerador?
b) Qual o trabalho líquido gerado, ou consumido, por este ciclo?
c) Caso esse ciclo descarregue 60 kJ para o reservatório frio, quanto ele recebe do reservatório quente?
Passo 1
Para responder a letra A basta ver se o ciclo está no sentido horário ou anti-horário. Como está no sentido horário o trabalho líquido é positivo, ou seja, trata-se de um motor. Isso acontece porque a área abaixo da reta AB (trabalho positivo pois é uma expansão) é maior do que a área abaixo da reta CD (trabalho negativo pois é uma compressão).
Passo 2
O trabalho líquido será igual a área do gráfico P x V.
Passo 3
Como trata-se de um motor temos que o equilíbrio de energia é igual a
Portanto,
Resposta
a) Motor
b) 40 kJ
c) 100 kJ
Exercício Resolvido #8
Lista 1 1a Lei da Termodinâmica MPEF, UFRJ, 2018/1 Questão 3
Um gás ideal é levado de um estado inicial A a outro estado B e depois para C. Por fim, o sistema é trazido de volta até A conforme diagrama p × V a seguir.
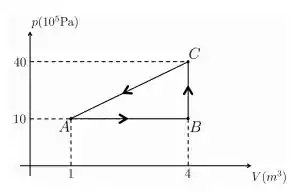
a) Escreva na tabela os sinais +, − ou 0 (zero) das grandezas termodinâmicas associadas a cada processo.
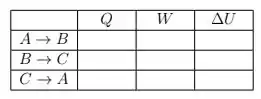
b) Calcule o trabalho realizado pelo sistema durante o ciclo.
c) Ao final de um ciclo completo, qual foi a quantidade total de calor transferida? O sistema recebeu, cedeu ou nem recebeu nem cedeu calor?
Passo 1
Primeiro é muito importante observar que este ciclo é de um refrigerador, isso pode ser visualizado pelo fato das setas estarem no sentido anti-horário. Sob o ponto de vista do trabalho temos que o trabalho realizado pelo gás de A até B é positivo e é dado pela área embaixo da reta AB, enquanto o trabalho realizado pelo gás de C até A é negativo e é definido pela área embaixo da reta CA. Contudo não precisamos calcular os dois trabalhos, basta o trabalho líquido que é negativo e é igual a área do triângulo ABC.
Passo 2
Para analisar a energia interna é importante lembrar que a energia interna é função apenas da temperatura logo quanto maior a temperatura maior a energia interna. Como a equação de Clapeyron nos fornece que
Basta vermos qual é o maior produto e esse terá a maior temperatura.
A –
B –
C –
Logo a ordem crescente de temperaturas é C-B-A.
Passo 3
Finalmente o calor que basta lembrar da 1ª lei da termodinâmica
No caminho BC não há trabalho logo
No caminho AB o volume aumenta a pressão constante logo o gás recebe calor, logo
Para o caminho AC podemos traçar duas adiabáticas sobre os pontos e fazer uma análise gráfica
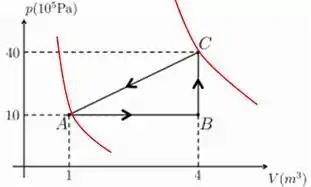
Como de C para A a adiabática se torna mais próxima da origem, então o gás perdeu calor para o ambiente
Passo 4
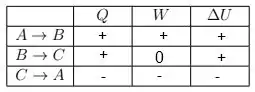
Vamos colocar a resposta na tabela
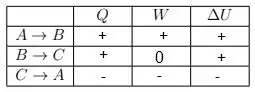
Passo 5
O trabalho realizado pelo ciclo é o trabalho líquido que é igual à área do triângulo, porém negativo por estar no sentido anti-horário.
Passo 6
Se ao final de um ciclo completo a variação da energia interna é zero, temos que:
Ou seja, ao final do ciclo o gás perdeu calor para o ambiente.
Resposta
Exercício Resolvido #9
Gordon Van Wylen, Richard Sonntag e Claus Borgnakke, Fundamentos da termodinâmica clássica, Tradução da 4ª ed. americana. São Paulo: Edgard Blucher, 1995, pp.251 – Exemplo 9.2 (Adaptado)
Vapor d’água é utilizado num determinado ciclo como fluido de trabalho. Sabendo que a variação de entalpia do vapor d’água ao passar pela caldeira é de 3017,8 kJ/kg e a variação de entalpia na bomba e na turbina são, respectivamente, 4 kJ/kg e 1069,5 kJ/kg. Calcule o rendimento dessa máquina.
Passo 1
É muito importante perceber que todos os dados da questão estão em função da entalpia específica , e isso é muito bom porque a variação da entalpia específica nos fornece exatamente o trabalho específico consumido na bomba e gerado na turbina, assim como o calor trocado com a fonte quente na caldeira.
Passo 2
Logo podemos escrever que
Passo 3
Substituindo na equação da eficiência
É importante lembrar que estamos falando de trabalho e calor específicos, ou seja, são o trabalho e calor divididos pela massa. Por isso estão com letras minúsculas.
Resposta
Exercício Resolvido #10
Elaboração própria
Um motor térmico opera segundo um certo ciclo termodinâmico, representado abaixo. Calcule a eficiência desse ciclo utilizando as entalpias fornecidas. Considere que os processos no evaporador e no condensador são isobáricos e na bomba e turbina adiabáticos.
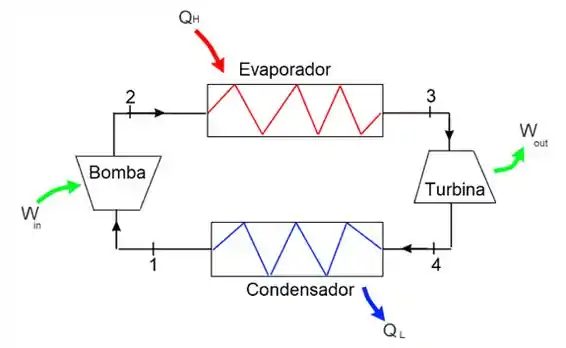
Passo 1
Para resolver esse problema a gente tem que lembrar que a diferença de entalpia num processo isobárico é igual ao calor transferido. Portanto:
Aqui vale a observação de que estamos utilizando os calores específicos e porque foi fornecida a entalpia específica .
Passo 2
Calcular os calores específicos:
Passo 3
A eficiência, para um ciclo motor é dada da forma:
Observe que o trabalho frio, por ser um trabalho que sai do sistema, é negativo. Mas a fórmula já considera isso, portanto, não podemos colocar , ok?
Resposta
Exercício Resolvido #11
Elaboração própria
Um motor térmico opera segundo um certo ciclo termodinâmico, representado abaixo. Calcule a potência deste ciclo sabendo que a vazão mássica do fluido de trabalho é igual a . Considere que os processos no evaporador e no condensador são isobáricos e na bomba e turbina adiabáticos.
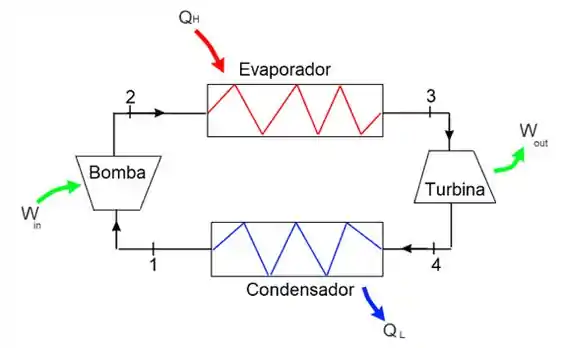
Passo 1
Para resolver esse problema a gente tem que lembrar que a diferença de entalpia num processo isobárico é igual ao calor transferido. Portanto:
Aqui vale a observação de que estamos utilizando os calores específicos e porque foi fornecida a entalpia específica .
Passo 2
Calcular os calores específicos:
Passo 3
Aplicando a primeira lei para ciclos:
Passo 4
Mas a gente acabou de calcular o trabalho específico, para achar a potência basta multiplicar pela vazão mássica de :