Ciclo de Carnot
Produzido por Rafael Cardoso BrandãoTeoria
O ciclo de Carnot é um ciclo reversível e ideal executado por uma máquina térmica e seu objetivo é a transformação de calor em trabalho da forma mais eficiente possível, a partir de transformações termodinâmicas em um fluido de trabalho.
Na figura abaixo você pode ver as transformações termodinâmicas que ocorrem no Ciclo de Carnot:
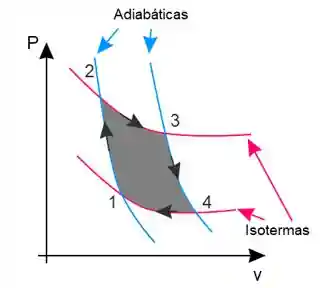
Postulados de Carnot
Lá em cima, quando eu disse que no Ciclo de Carnot temos “transformação de calor em trabalho da forma mais eficiente possível”, eu não estava exagerando!
Esse é um dos postulados de Sadi Carnot! 👇👇👇
“Nenhuma máquina operando entre duas temperaturas fixadas pode ter rendimento maior que a máquina ideal de Carnot, operando entre essas mesmas temperaturas”
Outra coisa importante do Ciclo de Carnot é que ela tem a mesma eficiência pra diferentes fluidos. Olha o que Carnot diz:
“Ao operar entre essas duas temperaturas, a máquina ideal de Carnot tem o mesmo rendimento, qualquer que seja o fluido operante”.
Ou seja, a Máquina de Carnot é a máquina mais top das máquinas térmicas (pena que ela não existe na vida real 😢).
Etapas do Ciclo de Carnot
Chegou a hora de você finalmente entender como funciona o ciclo de Carnot, sem enrolação!
Dá uma olhada nesses esqueminhas do Ciclo de Carnot:
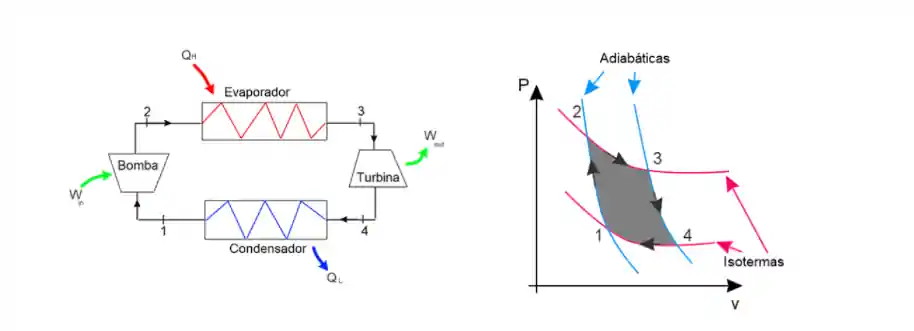
Processo 1-2: Compressão Adiabática
Essa é a primeira etapa do Ciclo de Carnot e ela acontece em uma bomba, para isso precisamos do trabalho mecânico da bomba
Então, nessa etapa o fluido de trabalho sofre uma compressão adiabática. Isso significa que durante esse processo não há troca de calor com o ambiente. Mas essa vai ser nossa única constante! Durante a compressão o volume diminui, a pressão aumenta e a temperatura aumenta até chegar na temperatura da fonte quente
Para essa etapa acontecer,
Processo 2-3: Expansão Isotérmica
O processo de expansão isotérmica ocorre no evaporador, e como o próprio nome indica, o volume do fluido aumenta, mantendo a temperatura
O objetivo dessa etapa é que o fluido receba o calor do evaporador
Processo 3-4: Expansão Adiabática
Saímos do evaporador e agora temos um fluido super quente
Essa é a hora do fluido brilhar! 🤩
A medida que o fluido passa pela turbina ele se expande ainda mais, mas ele não perde calor! O que acontece é uma queda da temperatura para
Processo 3-4: Compressão Isotérmica
Na etapa anterior o fluido desempenhou o seu principal objetivo, que é gerar trabalho! Então agora temos que deixar ele em condição de voltar pra etapa inicial e um novo ciclo começar!
Então agora temos uma compressão isotérmica onde o o fluido de trabalho condensa perdendo calor para a fonte fria
Agora o fluido volta para a bomba e vai seguindo cada etapa de novo!
Eficiência do Ciclo de Carnot
Como a gente viu lá em cima, nenhum ciclo possui uma eficiência maior do que a de Carnot, portanto, ao saber a eficiência do ciclo de Carnot podemos saber a eficiência máxima teórica de qualquer outro ciclo!
A eficiência de uma máquina térmica pode ser calculada da seguinte forma:
Mas o trabalho
Mas o Ciclo de Carnot é um ciclo reversível! Então podemos usar a seguinte relação:
Logo a eficiência pode ser dada com base apenas nas temperaturas da fonte fria e da fonte quente, lembrando que a temperatura deve estar na escala Kelvin, ou outra escala absoluta!
Aplicando o mesmo conceito para refrigeradores e bombas de calor, funcionando num ciclo de Carnot vamos ter:

Exemplo: Qual é a eficiência máxima de uma máquina que funciona entre temperaturas de 20°C e 150°C?
Como vimos, a eficiência máxima de uma máquina térmica é igual a eficiência de Carnot. Então vamos usar a seguinte fórmula:
Como as temperaturas devem estar em Kelvin, temos que:
Agora sim, podemos substituir:
Ou também podemos escrever em porcentagem:
Podemos ir um pouquinho mais adiante e ver qual seria o trabalho fornecido por esta máquina se o calor recebido pela fonte quente fosse igual a
Substituindo:
Pelo balanço de energia também podemos saber a quantidade de calor dispensada para a fonte fria.
Awee!!
Vídeo Aula - Ciclo de Carnot
Ficou com alguma dúvida sobre o Ciclo de Carnot?! Então se liga nesse vídeo 👇
Vamos praticar com exercícios?!
Etapas do Ciclo de Carnot
Eficiência do Ciclo de Carnot
Vídeo Aula - Ciclo de Carnot
Exercícios Resolvidos
Exercício Resolvido #1
Elaboração própria
Quais os processos envolvidos num ciclo de Carnot?
Passo 1
Os processos envolvidos no ciclo de Carnot são duas adiabáticas e duas isotermas. Como representado no diagrama abaixo:
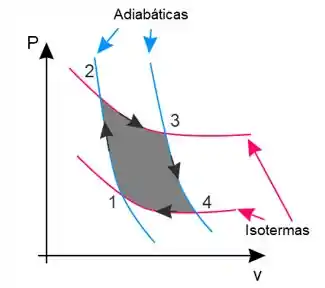
Passo 2
Além disso podemos visualizar o ciclo prático como na figura abaixo, onde as adiabáticas ocorrem na bomba e na turbina e as isotermas ocorrem no condensador e no evaporador.
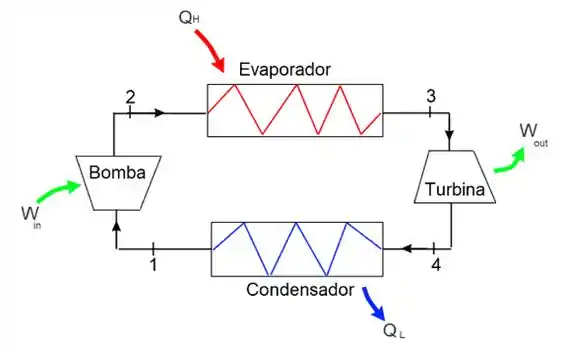
Resposta
Ei, a resposta está no passo a passo :)
Exercício Resolvido #2
Formulação própria
Um cientista afirma ter inventado uma máquina que opera segundo um ciclo termodinâmico entre as temperaturas de 27°C e 127°C e que possui eficiência de 55%. Isso é possível?
Passo 1
Neste problema o enunciado nos fornece apenas as temperaturas da fonte quente, da fonte fria e a eficiência. Logo é muito provável ser um problema envolvendo o ciclo de Carnot, ao perguntar se este ciclo é possível essa ideia se confirma porque nenhum ciclo pode ter a eficiência maior do que a do ciclo de Carnot.
Passo 2
Então vamos calcular a eficiência do ciclo de Carnot que opera entre as mesmas temperaturas.
Passo 3
Ao comparar a eficiência de Carnot (25%) com a fornecida pelo problema (55%) percebemos que a eficiência da máquina do cientista é maior do que a do ciclo de Carnot. Logo isso é impossível.
Resposta
Esse ciclo é impossível.
Exercício Resolvido #3
Lista 2 - 2a Lei da Termodinâmica MPEF, UFRJ, 2018/1 Questão 1
Uma máquina térmica utiliza o calor fornecido por uma fonte para realizar trabalho. Nos motores de automóvel a mistura gasolina-ar atua como substância de trabalho. A temperatura máxima atingida pela explosão do combustível no interior de um cilindro pode variar em função de diferentes fatores. Podemos considerar que em um determinado motor a mistura gasolina-ar atinja TQ = 1200 K após a combustão e que a temperatura do meio ao redor dos cilindros desse motor seja TF = 400 K. Qual seria o rendimento máximo para uma máquina que opera entre essas temperaturas?
Passo 1
Lembre-se que sempre quando o problema pedir o rendimento máximo de uma máquina qualquer quer dizer que o problema quer o da máquina de Carnot.
Como o problema nos forneceu TH e TL que nesse exercício são simbolizados por TQ e TF, respectivamente. Basta aplicar na equação da eficiência de uma máquina de Carnot.
Passo 2
Aplicando na equação
Resposta
Exercício Resolvido #4
Lista 2 - 2a Lei da Termodinâmica MPEF, UFRJ, 2018/1 Questão 2
A seguir, estão representadas duas máquinas térmicas (I e II).
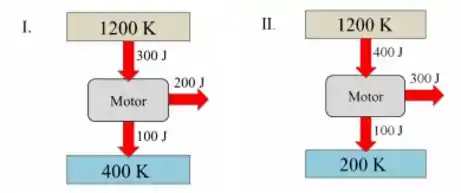
a) Qual é o rendimento de cada uma das máquinas?
b) Uma delas corresponde a uma máquina de Carnot. Qual?
Passo 1
Para calcular o rendimento fazemos uma divisão entre o que eu quero pelo que eu gasto, lembrando que são dois motores (é possível perceber isso porque o trabalho “sai” do sistema).
Passo 2
Para motores a eficiência é calculada como
Para I
Para II
Passo 3
Agora existem dois meios de ver se a máquina é de Carnot, o primeiro e mais fácil de lembra é simplesmente calcular a eficiência pela fórmula da eficiência de Carnot e comparar com as do resultado anterior. Onde
Para I
Para II
Ficou claro que o motor I é um motor de Carnot. Porém existe um jeito bem mais rápido de fazer isso. Basta se ligar na seguinte proporção, que é válida para ciclos de Carnot:
Para I
Para II
Resposta
a)
b) Máquina I
Exercício Resolvido #5
Gordon Van Wylen, Richard Sonntag e Claus Borgnakke, Fundamentos da termodinâmica clássica, Tradução da 4ª ed. americana. São Paulo: Edgard Blucher, 1995, pp.157 – 6.12.
Propõe-se aquecer uma residência durante o inverno usando uma bomba de calor. A temperatura da residência deve ser mantida igual a 20°C. Estima-se que, quando a temperatura do meio externo cai a -10°C, a taxa de transferência de calor da residência para o meio externo seja de 25kW. Qual a mínima potência elétrica necessária para acionar essa bomba de calor?
Passo 1
De novo o problema não cita explicitamente qual ciclo termodinâmico na qual a bomba de calor opera e pede a potência mínima de operação, portanto, vamos calcular essa potência baseada num ciclo de Carnot.
Passo 2
Para isso vamos calcular a eficiência do ciclo, que como sabemos depende apenas das temperaturas da fonte quente e da fonte fria
Passo 3
Associamos essa eficiência a perda de calor que a casa sofre para o ambiente para achar a potência.
Resposta
Exercício Resolvido #6
UNICAMP, lista de termodinâmica.
Uma bomba de calor opera segundo o ciclo de Carnot segundo o diagrama a seguir.
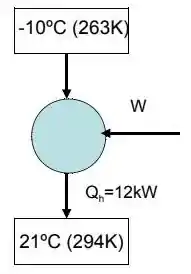
Calcule o trabalho necessário para a operação dessa bomba de calor.
Passo 1
Para achar o trabalho basta achar ou a eficiência ou o . Aqui irei resolver utilizando a relação entre os calores e temperaturas. Lembre-se que essa relação é válida utilizando a escala absoluta e para o ciclo de Carnot.
Passo 2
Pela primeira lei da termodinâmica
Resposta
Exercício Resolvido #7
Lista UNICAMP
Uma máquina de Carnot funciona segundo o diagrama a seguir.
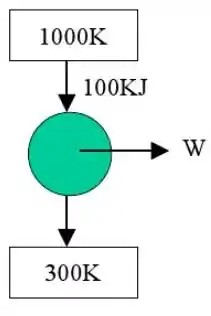
Calcule o trabalho fornecido por esta máquina e a quantidade de calor transmitido ao reservatório frio.
Passo 1
Como estamos falando de uma máquina de Carnot podemos utilizar a relação para eficiência dada por
Passo 2
Porém a eficiência pode, também ser calculada como
Logo
Passo 3
Pela aplicação da primeira lei ao sistema:
Resposta
Exercício Resolvido #8
Formulação própria
Um refrigerador utiliza o ciclo de Carnot para manter uma câmara frigorífica a temperatura de -10°C. Sabendo que esse refrigerador descarrega calor para um ambiente a temperatura de 20°C, qual é a eficiência desse refrigerador, sabendo que utiliza um trabalho de 2kJ por ciclo?
Passo 1
Vamos ver os dados fornecidos pela questão
- Temperatura da fonte fria
- Temperatura da fonte quente
- Trabalho
- Temperatura da fonte fria
- Temperatura da fonte quente
Com isso a questão pede a eficiência do refrigerador. Lembre-se que quando falamos de eficiência estamos falando de uma razão entre o que queremos sobre o que gastamos. Como trata-se de um refrigerador queremos retirar calor de um ambiente mais frio às custas de trabalho fornecido ao refrigerador. Isso pode ser visto numa equação como
Passo 2
Show de bola! O problema já até nos forneceu o trabalho fornecido ao ciclo, falta agora o calor retirado da fonte fria .
Repare que as temperaturas dos reservatórios quente e frio foram dadas, agora basta lembrar da relação entre temperaturas e calores, que é válida apenas para ciclos de Carnot:
Lembrando, também, que as temperaturas devem estar na escala absoluta (Kelvin)
Passo 2
Agora temos o calor frio em função do calor quente. Como num refrigerador o balanço de energia é dado por
Basta substituir na equação acima e achar
Passo 3
Por fim basta calcular a eficiência
Resposta
Sim, a eficiência de um refrigerador pode ser maior do que 1.
Exercício Resolvido #9
Gordon Van Wylen, Richard Sonntag e Claus Borgnakke, Fundamentos da termodinâmica clássica, Tradução da 4ª ed. americana. São Paulo: Edgard Blucher, 1995, pp.158 – Exercício 6.28
Propõe-se construir uma central termoelétrica com potência de 1000 MW e utilizando vapor e água como fluido de trabalho. Os condensadores devem ser resfriados com água de um rio ver (figura abaixo). A temperatura máxima do vapor será de 550 °C e a pressão nos condensadores será de 10 kPa. Como consultor de engenharia, você é solicitado a estimar o aumento da temperatura na água do rio (entre montante e jusante da usina). Qual é a sua estimativa? Calcule o trabalho necessário para a operação dessa bomba de calor. Considere que a central opere num ciclo de Carnot. Dados:
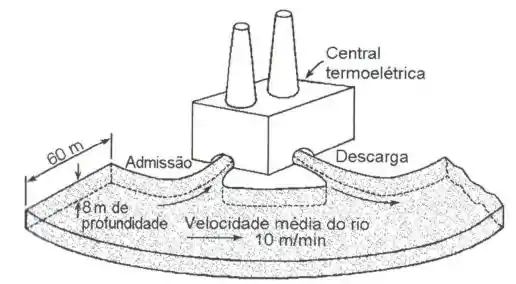
Passo 1
Primeiro vamos ver os dados que nos foram dados desta questão. Referente à própria central termoelétrica temos:
Com relação ao rio temos os seguintes dados:
- Profundidade = 8 metros.
- Largura = 60 metros.
Para calcular a variação de temperatura temos de estimar a massa que corre no rio e a quantidade de calor rejeitado no rio . Vamos começar calculando .
Passo 2
Como temos a quantidade de trabalho realizado por segundo (), se calcularmos a eficiência deste ciclo poderemos saber , e também , embora não seja relevante neste problema.
Então vamos calcular a eficiência deste ciclo de Carnot que, como sabemos, é fornecida pela equação
Mas agora olha que mas não foi dado. Mas tem o detalhe que, no condensador, a pressão é de 10 kPa, então vamos lá na tabela da água saturada e vemos que a água a pressão de 10 kPa condensa a 45,81°C.
Agora podemos calcular a eficiência, com as temperaturas em Kelvin!
Passo 3
Agora podemos achar o , lembrando que a eficiência também é dada por
Que se dividirmos pelo tempo em cima e embaixo vamos ter uma relação de potência e taxa de transmissão de calor, ao invés de trabalho e calor.
Aqui podemos fazer um pouco de álgebra para eliminar o e achar direto ou, como farei agora, calcular ambos.
Para achar utilizamos a primeira lei da termodinâmica para ciclos (de novo dividindo tudo pelo tempo):
Passo 4
No passo 3 conseguimos achar o calor transferido para o rio por segundo. Com isso vamos calcular a vazão mássica do rio, também por segundo né pra fazer algum sentido! haha.
Lembrando lá de fentran ou mecflu temos que a vazão mássica é dada por
Considerando a massa específica , e temos
Passo 5
Agora ficou facinho, basta fazer o famoso Mr. cat, para calcular a variação de temperatura.
Obs: Aqui vai uma observação legal. Preste sempre atenção nas unidades! Viu que se dividirmos pelo tempo dos dois lados (ou em cima e embaixo como no passo 3) a unidade continua igual e temos uma taxa de alguma grandeza, ou seja, aquela grandeza pelo tempo, que é representado com um pontinho em cima da unidade.
Resposta
Exercício Resolvido #10
Elaboração própria
Uma brilhante aluna de termodinâmica, ao refletir sobre o ciclo de Carnot, teve o seguinte questionamento ao ver o funcionamento do condensador e evaporador: “A troca de calor acontece quando há diferença de temperaturas, então como é possível existir um processo de troca de calor a temperatura constante?”
Após algum tempo a aluna chegou na conclusão correta, qual foi sua conclusão?
Passo 1
A conclusão da nossa brilhante aluna foi de que o Ciclo de Carnot, por ser um ciclo ideal e hipotético (impossível de ocorrer na prática) poderia realizar trocas de calor com diferenças de temperaturas infinitesimais.
Passo 2
Peguemos dois exemplos de motores, um ideal de Carnot e outro real, ambos com temperaturas da fonte quente e fria iguais a 100°C e 20°C, respectivamente.
O fluido de trabalho que percorre o motor real irá trocar calor com a fonte quente a uma temperatura de 70°C (30 graus de diferença) e com a fonte fria a 25°C (5°C de diferença).
Já o fluido que percorre o Ciclo de Carnot irá trocar calor com a fonte quente a uma temperatura de 99,99°C (0,01°C de diferença) e com a fonte fria a 20,01°C (0,01°C de diferença).
Passo 3
Como essa diferença de temperatura é minúscula então podemos falar que o processo é isotérmico, é por esse motivo também que o Ciclo de Carnot é dito reversível pois a diferença de temperatura, nas trocas de calor, tende a zero.
E é exatamente por isso que o Ciclo de Carnot não existe de fato, apenas hipoteticamente, porque diferenças de temperatura tão pequenas não sustentam um motor térmico.
Resposta
Ei, a resposta está no passo a passo :)