Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Termodinâmica - Çengel - Termodinâmica - Ed: 7º - Capítulo 7.Problemas - Ex. 100

100. Um tanque com volume constante contém 5   k g de ar a 100   k P a e 327   ° C . O ar é resfriado até a temperatura da vizinhança, equivalente a 27   ° C . Considere calores específicos constantes de 300   K . (a) Determine a variação da entropia do ar no tanque durante o processo, em   k J / K ,

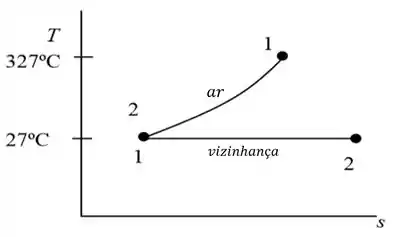
(b) determine a variação líquida da entropia do universo decorrente desse processo, também em k J / K , e (c) represente graficamente os processos para o ar do tanque e para a vizinhança em um diagrama T - s . Não se esqueça de rotular os estados inicial e final para ambos os processos.

Passo 1

Bora fazer mais uma questãozinha sobre entropia!

Olha só! Da tabela A - 2 a , sabemos que à temperatura ambiente de 300   K , o ar tem as seguintes propriedades...

c p = 1,005   k J / ( k g ⋅ K )

c v = 0,718   k J / ( k g ⋅ K )

Passo 2

a) Sendo assim! Vamos pro que interessa!

Olha só! Apesar de considerarmos o ar com um gás ideal como nos problemas anteriores, desta vez iremos tratá-lo como uma substância incompressível.

De modo que a variação de entropia para ele, é dada pela fórmula abaixo...

s 2 - s 1 = c p ln ⁡ T 2 T 1

∆ s a r = c p ln ⁡ T 2 T 1

T 1 é igual à...

T 1 = 327 + 273   K

T 1 = 600   K

E T 2 é igual à...

T 2 = 27 + 273   K

T 2 = 300   K

Sendo assim, obtemos que:

∆ s a r = ( 1,005   k J / ( k g ⋅ K ) ) ln ⁡ 300 600

∆ s a r = ( 1,005   k J / ( k g ⋅ K ) ) ln ⁡ 300 600

∆ s a r = - 0,6966   k J / ( k g ⋅ K )

Como temos uma massa de 5   k g , então a variação de entropia relativo à essa massa é igual à...

∆ s a r = - 2,488   k J / K

Passo 3

b) Tomemos o conteúdo do tanque como sistema. Este é um sistema fechado, pois nenhuma massa entra ou sai.

Sendo assim, o balanço de energia para este sistema fechado estacionário pode ser expresso como...

E ˙ e n t r a d a - E ˙ s a í d a ⏟ E n e r g i a   l í q u i d a   t r a n s f e r i d a   p o r   c a l o r ,   t r a b a l h o   e   m a s s a = ∆ E ˙ s i s t e m a ⏟ V a r i a ç ã o   d a s   e n e r g i a s   i n t e r n a ,   c i n é t i c a ,   p o t e n c i a l ,   e t c

Bom! Temos algumas hipóteses que podem ser levantadas para esse nosso problema... As energias cinética e potencial são desprezíveis... Ou quem sabe, o tanque possa ser adiabático...

Ou quem sabe o processo pode ser reversível.

Mas quem se importa, né! Em todo problema até agora, a gente só faz uma coisa, igualar a energia do sistema a zero.

∆ E ˙ s i s t e m a = 0

E consequentemente...,

E ˙ e n t r a d a - E ˙ s a í d a = 0

E ˙ e n t r a d a = E ˙ s a í d a

Ficamos então,com...

E ˙ e n t r a d a = E ˙ s a í d a

m ˙ h 1 = Q ˙ s a í d a + m ˙ h 2

Q ˙ s a í d a = m ˙ h 1 - m ˙ h 2

Como o ar é resfriado a volume constante, h 1 e h 2 podem ser escritos como...

h 1 = c v T 1

h 2 = c v T 2

Agora, é só colocar essas duas relações na fórmula de antes...

Q ˙ s a í d a = m ˙ c v ( T 1 - T 2 )

E substituindo os valores numéricos adequados, obtemos a quantidade de energia gerada na saída...

Q ˙ s a í d a = ( 5   k g ) ( 0,718   k J / ( k g ⋅ K ) ) ( 600   K - 300   K )

Q ˙ s a í d a = 1077   k J

E para obter a alteração da entropia na vizinhança do nosso sistema, basta dividir essa quantidade de energia na saída pela temperatura final...

∆ S v i z i n h a n ç a = 1077   k J 300   K

∆ S v i z i n h a n ç a = 3,59   k J / K

Finalmente, para encontrar a variação líquida da entropia do universo, basta somar as duas entropias que obtemos...

∆ S u n i v e r s o = ∆ s a r + ∆ S v i z i n h a n ç a

∆ S u n i v e r s o = - 2,488   k J / K + 3,59   k J / K

∆ S u n i v e r s o = 1,10   k J / K

Passo 4

c) Pra finalizar, aqui está o gráfico representando os processos para o ar do tanque e para a vizinhança.

Resposta

a)

∆ s a r = - 2,488   k J / K

b)

∆ S u n i v e r s o = 1,10   k J / K

c)

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

O oxigênio do Prob. 16 – 35 é substituído por ar. Compare a transferência total de calor necessária (em k J / k g ) para aquecer esse ar da mesma maneira, (a) desprezando e (b) incluindo a dissociação
Ar (composto por 79 % de N 2 e 21 % de O 2 ) é aquecido a 2.000K a uma pressão constante de 2a t m . Considerando que a mistura de equilíbrio consiste em N 2 , O 2 e N O , determine a composição de eq
Um tanque com volume constante contém uma mistura de 1k m o l de H 2 e 1k m o l deO 2 a 25° C e 1a t m . O conteúdo é então inflamado. Determine a temperatura e a pressão finais do tanque, considerand
Mostre que, enquanto a extensão da reação ( α ) para reação de dissociação X 2 ⇌ 2 X é menor que um, α é dado por: α = K p 4 + K p
Um k m o l de oxigênio a 1a t m e298K é aquecido para 10a t m e 2.200K . Calcule a quantidade total de transferência de calor necessária, em k J / k m o l , caso (a) a dissociação seja desprezada e (b