Enunciado
Termodinâmica - Çengel - Termodinâmica - Ed: 7º - Capítulo 7.Problemas - Ex. 92
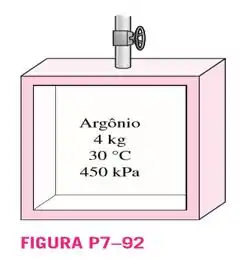
92. Um tanque rígido isolado contém de gás argônio a . Uma válvula é então aberta, e o argônio escapa até que a pressão interna caia para . Considerando que o argônio remanescente no tanque tenha passado por um processo reversível e adiabático, determine a massa final no tanque.
Passo 1
Bora fazer mais uma questãozinha sobre entropia!
Olha só! Em condições especificadas, o argônio pode ser tratado como um gás ideal. Que é o nosso caso aqui, né não!?
Afinal, praticidade é tudo que a gente quer!
Então, uma vez que temos que todo esse processo pelo qual passa o argônio, é dado como reversível e adiabático e, portanto, é um processo isentrópico.
Sendo assim, as relações isentrópicas de gases ideais vão se aplicar.
Passo 2
No livro, tiramos que a razão específica de calor do gás argônio é...
Mas porque precisaremos dessa constante!?
Ora bolas! Porque para as relações isentrópicas de gases ideais, temos a seguinte equação...
é a temperatura na qual o argônio está inicialmente. Só que precisamos passar ela de para .
Fácil, né não!? Basta somar com ... Desse jeito aqui:
A pressão vale e a pressão vai valer .
Sendo assim...
Passo 3
Para finalizar e determinar a massa final de argônio, basta usar a velha relação dos gases ideais...
Bom! O volume não vai se alterar. É o volume do recipiente! Então...
E o número de mols é dado pela divisão da massa pela massa molar. Como a massa molar não se altera, então nossa equação de cima vai ficar assim...
Substituindo os valores numéricos de cada variável...
Conseguimos obter nossa resposta!