Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Termodinâmica - Van Wylen- Ed: 6º - Capítulo 6.Problemas - Ex. 125

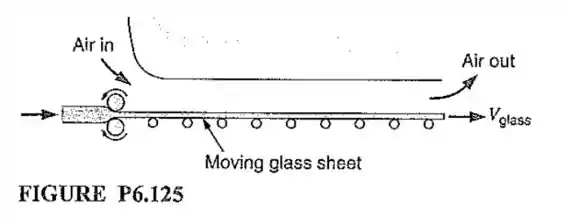
125 - In a glass factory a 2   m wide sheet of glass at 1500   K comes out of the final rollers that fix the thickness at 5   m m with a speed of 0.5   m / s (see F i g   P 6.125 ) . Cooling air in the amount of   20   k g / s comes in at 17   ° C from a slot   2   m wide and flows parallel with the glass. Suppose this setup is very long so the glass and air comes to nearly the same temperature (a coflowing heat exchanger) what is the exit temperature?

Passo 1

Fala meus industriais, vamos projetar nosso protótipo de esteira para a nossa fábrica? Cola aqui então!

Sabendo que estamos interessados na quantidade de energia potencial que há na entrada e saída tanto do vidro quanto no ar então a equação do balanço de energia no processo é:

∑ E e n t r a d a = ∑ E s a í d a

m ˙ a r   e n t r a d a h a r   e n t r a d a + m ˙ v i d r o   e n t r a d a h v i d r o   e n t r a d a

= m ˙ a r   s a i d a h a r   s a i d a + m ˙ v i d r o   s a i d a h v i d r o   s a i d a

E por se tratar de um sólido, então o escoamento do vidro será dado por:

m ˙ v i d r o = ρ A v

Onde a densidade do vidro é de 2500   k g / m 3 pela tabela A . 4 e v = 0.5   m / s e a área será 2 × 5 × 10 - 3 = 10 - 2   m 2 (como se passasse 2   m   em uma espessura de 5   m m ), logo:

m ˙ v i d r o = 2500 × 0.5 × 10 - 2 = 12.5   k g / s

E a entalpia vai ser dada por:

h = c p T

Para ficar mais fácil de saber as temperaturas em cada ponto

E os dados do enunciado são dados por:

m ˙ a r = 20   k g / s

T v i d r o   e n t r a d a = 1500   K

T a r   e n t r a d a = 273 + 17 = 290   K

c p   v i d r o = 0.8

c p   a r = 1.0035  

T   a r   s a i d a = T v i d r o   s a i d a

E as vazões mássicas são constantes pro vidro e pro ar

Passo 2

Calma muita coisa, vamos botar isso tudo na fórmula.

m ˙ a r   c p   a r T a r   e n t r a d a + m ˙ v i d r o c p   v i d r o T v i d r o   e n t r a d a

= m ˙ a r c p   a r T a r   s a i d a + m ˙ v i d r o c p   v i d r o T v i d r o   s a i d a

Então:

20 × 1.0035 × 290 + 12.5 × 0.8 × 1500 = 20 × 1.0035 T a r   s a i d a + 12.5 × 0.8 T v i d r o   s a i d a

T a r   s a i d a = T v i d r o   s a i d a = 692.4   K

E essa é a saída da temperatura tanto do vidro quanto do ar, já que o enunciado disse que eles são iguais.

É nós e obrigado!

Resposta

692.4   K

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

4- Como variam as vazões em massa e em volume num dispositivo que opera em regime permanente?
110- Um recipiente rígido, inicialmente em vácuo, é carregado com água, proveniente de uma tubulação, a 0.8M P a e 350° C . Admita que o processo de enchimento é adiabático e que o recipiente é lacrad
111- Ar a 800k P a e 20° C escoa numa tubulação principal e pode alimentar um tanque através de uma tubulação secundária com válvula (ver F i g6.111 ). O volume do tanque é igual a 25l i t r o s e, in
113- Um tanque rígido, com capacidade de 0.1m 3 , contém ar a 1M P a e 200° C . Uma válvula do tanque é aberta e o ar escoa para fora do tanque até que a pressão atinja 100k P a .Calor é transferido a
137- Um tubo de aço, com diâmetro externo igual a 100m m , é alimentado com 2k g / s de água líquida saturada a 1.0M P a . Gás de combustão a 1000K escoa por fora do tubo e proporciona um coeficiente