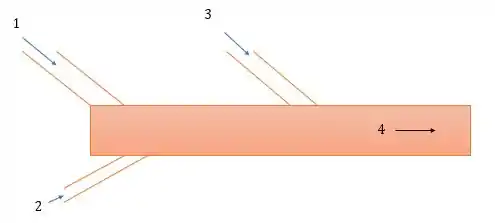
127- Três escoamentos de ar, todos com pressão de , são conectados ao mesmo duto de saída e eles se misturam sem interferência de nenhuma fonte de calor externa. O escoamento 1 tem vazão mássica de a , o escoamento tem uma vazão mássica de a e o escoamento tem vazão mássica de há uma temperatura de .

Ignore qualquer energia cinética e encontre a taxa de vazão volumétrica do sistema.

Com essa entalpia podemos descobrir variáveis importantes para encontrar a taxa da vazão volumétrica que é calculada por:

Só notar que a unidade dimensional é a mesma.

Ou seja, somente precisamos saber quanto vale o volume específico desse ar circulante, mas antes é bom sabermos a sua temperatura de saída e com isso pela tabela teremos:

Mas por que descobrir a temperatura da saída do duto? Bem... tenho uma notícia chata, na tabela não tem o volume específico né. E isso é esperado até por que para gases ideias nós temos uma fórmula que diz o comportamento para o volume específico

Só que você sabe como encontrá-la, eu só vou relembrar

Só isso

Então para nós teremos:

Então a vazão volumétrica será de:

Vamos para mais por que nunca podemos ficar tranquilos com menos.