Enunciado
Termodinâmica - Van Wylen- Ed: 6º - Capítulo 6.Problemas - Ex. 119
119- A mostra o esquema de uma turbina que é alimentada com a e . A descarga da turbina está ligada a um tanque com volume de , e que inicialmente está evacuado.
A operação da turbina termina quando a pressão no tanque atinge . Nesta condição, a temperatura do no tanque é . Admitindo que todos os processos são adiabáticos, determine o trabalho realizado pela turbina num processo de enchimento do tanque.
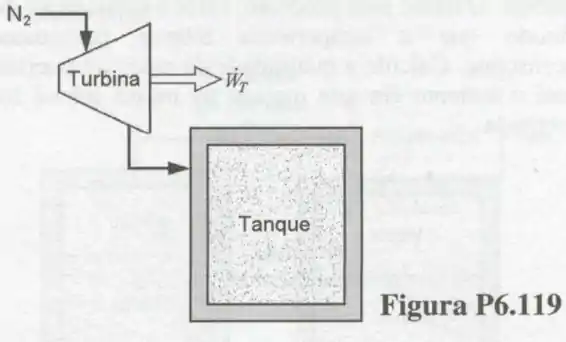
Passo 1
Fala nação do Responde Aí! Que alegria ter a sua companhia!
Hoje estamos aqui para mais uma questão, e ela é bem interessante, espero que te ajude :D
Modelando a energia que rola nessa turbina nós temos algo como
Ou seja, temos uma energia de entrada na turbina, uma parcela dela é convertida em trabalho e outra parte entra no tanque, ok até aqui né? Nada complexo
A questão aqui é o que são essas energias, bem a energia que entra na turbina gera trabalho mecânico e gera energia que será armazenada em um local então a energia de entrada é uma energia potencial (em gerar trabalho) e a energia que entra no tanque vira uma energia parada (como calor) digamos então o modelo ficaria da seguinte forma
E como o nitrogênio não sai por outro lugar então:
O que nos deixa com:
Uma forma de vermos a energia interna vs a entalpia é que a entalpia gera um trabalho enquanto a energia interna não. Aqui temos perfeitamente a definição entre ambas.
Então o trabalho realizado será de:
Passo 2
Agora chegou a hora de vermos tabelas! Afinal temos que calcular alguma coisa, e pra isso precisamos colher dados.
No estado inicial temos nitrogênio a
Na tabela temos as seguintes propriedades para o estado inicial
E no estado final temos:
Isso nos dá uma vazão mássica que entra no tanque de:
Portanto a energia interna que entra é de:
Passo 3
Então a potência da turbina será:
E é bem isso pessoal! Estaremos juntos.