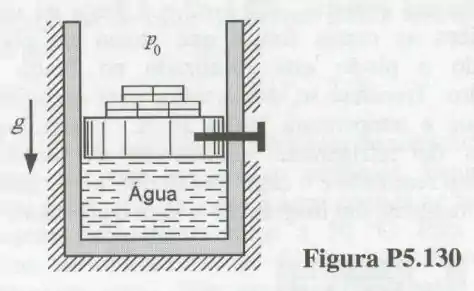
130- A mostra um cilindro isolado, que contém de água, e apresenta o pistão travado por um pino. Neste estado, a temperatura da água é e título igual a . A área da seção transversal do cilindro é , o pistão e os pesos tem uma massa total de . O pino é então removido, permitindo que o pistão se mova. Admitindo que o processo seja adiabático, determine o estado final da água.

Começando pela pressão que é mais de boas de achar.

De boas, pois sabemos que a água precisa aguentar a pressão atmosférica além da pressão exercida pela massa acima dela, então temos que:

Substituindo os valores temos:

Onde e como estamos trabalhando com temos que dividir por para termos o resultado que queremos senão estaremos a pressão da massa em

Se lembra do passo anterior? Então ... a pressão naquela equação é utilizando justamente de forma que teremos:

E uma forma de reescrevermos essa expressão de modo a utilizarmos ela é da seguinte forma:

E essa equação é igual a:

Já que a segunda equação tem todas os índices do segundo estado e batem com a equação que correlaciona entalpia e energia interna

A partir de agora temos diversas abordagens para o problema eu vou me focar agora em encontrar dados que são tabelados utilizando as tabelas que estão no final desse livro já que temos a pressão exercida na água no estado final (estado 2) além da temperatura e da titulação no estado inicial (ou estado 1).

Começando pelos dados do estado cuja água está a , pela tabela temos:

Dessa forma como a titulação então:

Então calculando a entalpia pela fórmula do passo anterior nós teremos:

Agora com esse valor de entalpia podemos verificar qualquer outra situação do estado pela tabela , pegando essa tabela rapidinho vemos que a temperatura está entre e , pois a entalpia calculada está entre esses dois valores

Fazendo a regra de três para encontrar o cruzamento da temperatura nós encontraremos:

E o volume especifico será de:

Com esses valores podemos também encontrar o volume específico e a energia interna no estado final.