Enunciado
Termodinâmica - Van Wylen- Ed: 6º - Capítulo 5.Problemas - Ex. 133
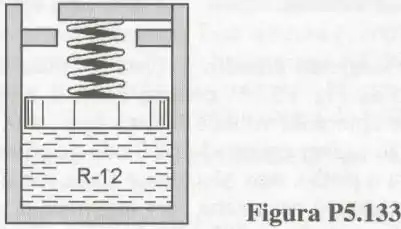
133- A mostra um conjunto cilindro-pistão que contém . Inicialmente, o volume da câmara é , a temperatura é e o título é igual a . O volume da câmara, quando o pistão encosta nos esbarros, é e a força da mola equilibra as outras forças que atuam no pistão quando o pistão está localizado no fundo do cilindro.
Transfere-se, então, calor para o conjunto até que a temperatura atinja . Determine a massa de refrigerante contida no conjunto, o trabalho realizado e o calor transferido no processo.
Faça, também, um diagrama para o processo.
Passo 1
Calma lá que ele pede quatro coisas para fazermos e se pegarmos tudo de uma vez no final não conseguiremos resolver nada.
Por partes...
Nenhuma massa é perdida no processo, então pela equação de energia temos que:
Ou seja, a energia interna da água no final do estado é a energia interna que ela tem inicialmente somado de um calor que é adicionado para ela subtraída de uma ajuda de trabalho externo.
Então vamos coletar dados do enunciado
No estado inicial 1 teremos:
Como estamos comentando aqui do líquido então pela tabela coletaremos:
Então pela titulação temos que o volume específico no estado inicial será:
Então a massa inicial do líquido será de:
E a energia interna será de:
Onde inicialmente a pressão que age no cilindro é puramente a pressão atmosférica, então a energia interna inicial será de:
Essa da massa responde a primeira pergunta das quatro, vamos para mais.
Passo 2
Ufa, pegamos tudo o que precisamos referente ao estado inicial, agora vamos para o estado final. Coletando o que o enunciado nos dá nós temos:
Mas precisamos da pressão no estado final para que fique tranquilo calcular o trabalho de expansão realizado! Bem calma, primeiro veremos o volume específico nesse estado já que nenhuma massa sai correndo do conjunto então:
Então temos a informação que o líquido tende a estabilizar com a temperatura de conjunto de com esse volume específico de acordo com a tabela vemos que a pressão então estará muito perto de de maneira mais exata ela estará próxima de:
Só que essa é a pressão que será chegada no final do experimento, quando a temperatura do líquido estiver em equilíbrio com o conjunto, mas o líquido consegue chegar no volume total ainda antes.
Como temos o trabalho sendo consumido por uma mola então seguramente temos uma variação linear da pressão e como o conjunto parte de e dobra seu volume então a pressão dobra por consequência sendo uma pressão de uma boa aproximação para essa pressão
Pela tabela essa pressão absoluta nos daria uma temperatura de saturação de:
Essa seria a temperatura correta do líquido quando o conjunto chega no batente. Depois a mola que se vire para suportar a pressão do líquido até chegar em , então o trabalho se daria pelo seguinte sistema:
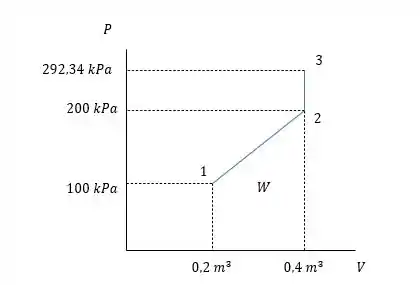
O trabalho seria de:
Nesse estado a energia interna do gás no estado 3 seria de:
Aqui usei a entalpia de mesmo, preguiça de fazer certinho (com a regra de três e talz). Espero que me perdoe o erro será pequeno.
Passo 3
Agora para o modelo de energia laaaaaa do primeiro passo:
Isolando que é o calor fornecido nós temos:
Agora se aplicarmos os valores que encontramos durante a questão nós temos:
O diagrama será muito parecido com o desenhado no passo anterior com a diferença que para o ponto teríamos o líquido superaquecido enquanto nos pontos e teríamos o líquido no seu estado saturado
Vamos para a próxima pessoal!