Enunciado
Termodinâmica - Van Wylen- Ed: 6º - Capítulo 12.Problemas - Ex. 53
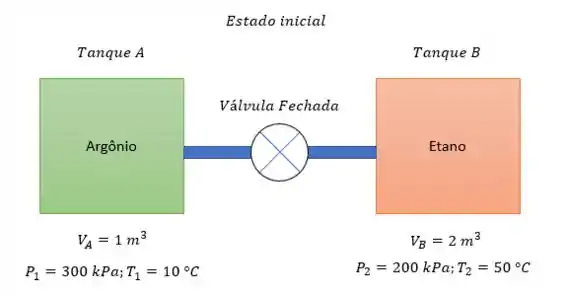
53- Dois tanques isolados, e , estão conectados por uma tubulação com válvula de controle. O tanque apresenta volume igual a e contém, inicialmente, argônio a e .
O tanque apresenta volume de e contém, inicialmente, etano a e . A válvula é aberta e assim permanece até que a mistura resultante atinja um estado uniforme.
Nestas condições, determine a pressão e a temperatura finais deste processo de mistura
Passo 1
Essa questão praticamente está pedindo em alto e bom som
Faça um desenho do que está sendo dito e seja feliz :D
Então vamos realizar esse pedido dela e liberar nossos dotes artísticos aqui
HAHAHAHAH, koé zoa não hahahahah
Voltando para a questão, como temos gases ideais nós podemos pegar os dados de suas constantes na tabela pois assim a aproximação será muito boa
Passo 2
Além desses dados nós podemos calcular as massas que cada gás ocupa em cada tanque pela fórmula
Então a massa das duas substâncias serão de:
O que nos dá uma massa total de gás igual a
Passo 3
Aí a válvula é aberta, os dois gases se misturam e pede-se quanto de temperatura e pressão se chega no sistema todo com o volume de
Sabendo que a equação do equilíbrio térmico é de:
Então:
Fazendo essa conta encontramos:
Passo 4
E agora para encontrar a pressão no estado final, bem se temos dois gases ideais sendo misturados então o resultado ainda continua sendo um gás ideal então a equação de Clapeyron ainda é válida, logo a pressão no estado final é de:
Onde o dessa mistura é proporcional com a massa das substâncias no total, ou seja:
Então:
E com isso matamos a questão, até a próxima pessoal, como brinde por chegar até aqui fique com esse meme
Você é daora cara :D