73- Ar está disponível numa tubulação a e . A tubulação está conectada a um tanque rígido, com volume de , através de uma tubulação secundária que contém uma válvula.
Inicialmente, o tanque contém ar na condição ambiente e . A válvula é, então, aberta e o ar da tubulação escoa para o tanque. O processo ocorre rapidamente e é essencialmente adiabático.
A válvula é fechada quando a pressão interna atinge um certo valor . Após o fechamento da válvula, o ar no tanque esfria até atingir a temperatura ambiente.
Neste estado, a pressão interna é . Qual é o valor da pressão ? Qual é a variação líquida de entropia para o processo global?
Passo 1
Tá decidido!

Eu vou fazer essa questão e meu compromisso é fazer com que você saia daqui feliz, contente e inspirado para fazer mais questões, até ser um aluno exemplar em sua faculdade, bora nessa? Acordo fechado? Então vamos
Vamos desenhar o estado inicial dessa questão
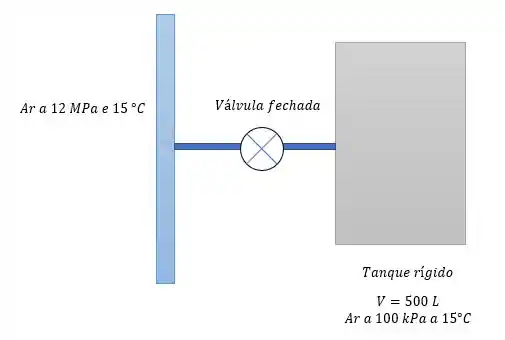
Nesse estado o estado inicial do ar dentro do tanque nos dá uma massa de ar igual a:
Já que o ar é um gás ideal, então sabendo que pela tabela então:
Pela mesma tabela temos
Esses valores serão importantes mais para frente pois podemos fazer
Passo 2
Aí a válvula é aberta e o ar que estava na linha com começa a entrar no tanque de forma que temos o segundo estado do ar dentro do tanque de forma que teremos
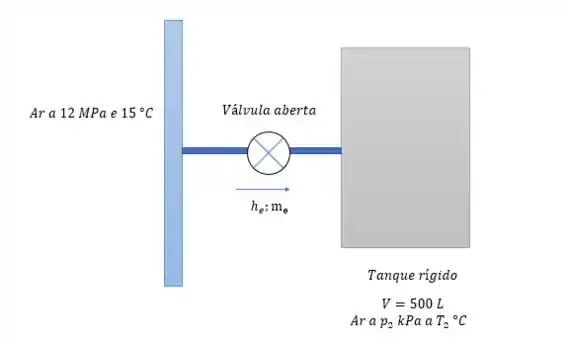
E aí vamos guardar esse estado no nosso cerebelo pois toda a questão se concentra nele, é como se tivéssemos um baú de tesouro na nossa frente, mas não temos a chave ainda, vamos pegar a chave no próximo estado
Passo 3
Aí a válvula é fechada com toda essa massa entrante de ar e atinge e pressão de dentro do tanque o que nos deixa com o seguinte estado 3.
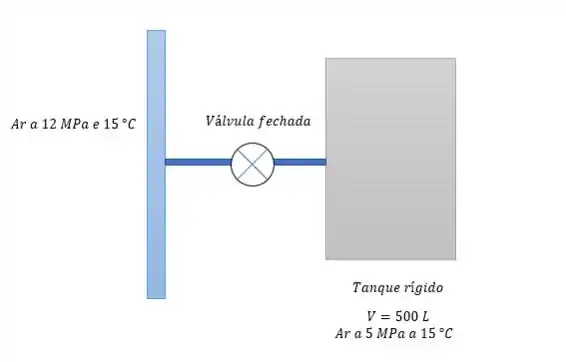
O que nos deixa com uma massa de ar dentro do tanque de:
Mas se lembra no passo que tínhamos uma massa de dentro do tanque? Então, isso quer dizer que a massa entrante é de:
Passo 4
Agora estamos começando a ver a chave que abre o tesouro que é a resolução da questão mas temos uma propriedade que ainda não está clara para a gente no estado que é a temperatura e ela é entrada pela diferença de calor que tem entre o ar nos dois estados dentro do tanque.
E essa transferência calor que é fornecido pelo ar que entra no tanque pode ser escrito como:
E como o processo é adiabático para a entrada desse ar então nenhum calor é perdido na entrada desse ar
Ou seja, o calor que existe no ar que entra no tanque é a diferença da energia interna do tanque antes e depois de ela entrar.
E como:
Então:
Isolando teremos:
Substituindo os valores nós teremos:
E com isso vamos direto calcular quanto vale a pressão nesse estado 2.
E assim abrimos o nosso baú de tesouro e ele tem

Metade do coração, pois a outra metade está comigo bebê :D Mentira, fiz essa analogia somente por que resolvemos metade da questão pois falta a entropia líquida gerada no processo todo.
Então vamos resolver isso
Passo 5
Para achar a entropia gerada em todo o processo temos que fazer:
Onde a entropia é a variação de entropia do estado inicial e final de dentro do tanque e diminuindo ainda do calor que entra no tanque e pela entropia que entra no tanque.
Mas antes precisamos saber o calor gerado por esse tanque em todo o processo (entre o estado 1 e o 3) e que será calculado por:
Entenda essa equação como, o calor gerado pelo tanque no processo todo (que seria a diferença de energia interna entre o estado inicial e final) é diminuído pelo calor que existe pelo ar que entra (como se o calor que entrasse atrapalhasse o calor gerado pelo tanque)
Diferente de quando o ar sai pelo tanque que ajuda na formação de calor do tanque.
Então substituindo os valores nessa fórmula:
E como a temperatura ambiente é de e para os gases ideais
Mas como em todos os estados da equação , então e como
Então podemos escrever a equação da entropia gerada como:
O que nos dá:
Substituindo os valores:
Agora temos o tesouro completo!

Ufa! Esse último passo foi brabo não vou mentir