Prove que o COP de todos os refrigeradores completamente reversíveis deve ser o mesmo quando as temperaturas do reservatório são também as mesmas.
Passo 1
Suponhamos que o refrigerador A é completamente reversível e que , no arranjo mostrado na figura a seguir.
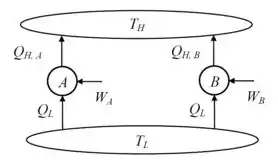
Temos que:
Isso significa que a magnitude do trabalho necessário para acionar o refrigerador B é menor do que o necessário para acionar o refrigerador A.
Passo 2
Aplicando a primeira lei aos rendimentos de ambos os refrigeradores temos:
Devido ao trabalho fornecido ao refrigerador B ser menor do que o fornecido ao refrigerador A e ambos terem o mesmo efeito de resfriamento, .
Passo 3
Como A é um refrigerador completamente reversível, podemos revertê-lo sem alterar a magnitude das transferências de calor e trabalho (como mostra a figura a seguir). O calor, , que é rejeitado pelo refrigerador invertido A, agora pode ser direcionado diretamente para o refrigerador B. Agora, nenhum calor é trocado com o reservatório .
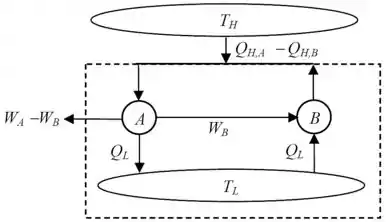
A magnitude do calor fornecido ao refrigerador reverso A, , demonstrou ser maior do que o rejeitado pelo refrigerador B. Existe então uma transferência líquida de calor do reservatório para o dispositivo combinado nas linhas tracejadas da figura cuja magnitude é dada por . Da mesma forma, há uma produção líquida de trabalho pelo dispositivo combinado cuja magnitude é dada pelo .
Concluindo, temos que o dispositivo cíclico combinado então troca calor com um reservatório a uma única temperatura e produz um trabalho que é claramente uma violação da declaração de Kelvin-Planck da segunda lei. Então a suposição de que deve estar errada.
Entretanto, se trocarmos A e B no argumento anterior, concluiremos que a não pode ser menor que a . A única alternativa que resta é que .
Resposta
A suposição de que deve estar errada. A única alternativa que resta é que .