Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Termodinâmica - Sonntag, R.E. e Borgnakke, C. -Fundamentos da Termodinâmica- Ed: 1º - Capítulo 8.Problemas - Ex. 36

Água a 1000   k P a e 250 ° C é levada ao estado de vapor saturado através de um processo adiabático em um conjunto cilindro-pistão. Determine a temperatura final, T , e o trabalho por unidade de massa. Estime o trabalho específico pela área no diagrama P-v e compare com o valor correto.

Passo 1

Fala pessoal, tudo certinho? vamos responder mais uma questão, então prepara o material e vamos responder!!

Primeiramente, nós temos as seguintes informações, fornecidos pelo enunciado

p 1 = 1000   k P a

T 1 = T 2 = 523,15   K

Primeiro vamos configurar duas equações principais necessárias para resolver este problema. Para calcular o trabalho necessário, usaremos a equação de energia para nossa massa de controle.

Q 2 = m u 2 - u 1 + W 2   ( 1 )

Para calcular o trabalho isobárico, usaremos a equação

s 2 - s 1 = q 2 T + s g e n   ( 2 )

Primeiro vamos obter algumas propriedades da amônia das tabelas. Da tabela B.1.3 correspondente a T 1 e p 1 obteremos o estado 1 volume específico, entropia e energia interna:

u 1 = 2709,91 k J k g

v 1 = 0,23268 m 3 k g

s 1 = 6,9246 k J k g   K

A seguir iremos para a tabela B.1.1 e obteremos a energia interna do vapor saturado correspondente a T 1 para verificar se nossa energia interna é maior que isso.

u g = 1522,00 k J k g

Nós podemos ver que

u 1 = 2709,91 > u g = 1522,00

O que significa que nossa substância está atualmente na região superaquecida!

Passo 2

No estado 2 sabemos que estamos em vapor saturado, então da tabela B.1.1 correspondente a T 2 e x 2 = 1 obteremos o volume específico do estado 2, entropia e energia interna:

p 2 = p s a t = 3973   k P a

u 2 = 2602,37 k J k g

v 2 = 0,05013 m 3 k g

s 2 = 6,0729 k J k g   K

Calculando a transferência de calor usando a equação (2):

s 2 - s 1 = q 2 T + s g e n ∙ T

Isolando o q 2 , nós temos que

q 2 = T s 2 - s 1 + 0

Fazendo a substituição dos termos,

q 2 = 523,15 6,0729 - 6,9246 = - 445,6 k J k g

Passo 3

Calculando o trabalho necessário usando a equação de energia (1):

w 2 = q 2 + u 1 - u 2

Novamente, substituindo os termos

w 2 = - 445,6 + 2709,91 - 2602,37

Com isso,

w 2 = - 338 k J k g

E o diagrama P-v é dado por

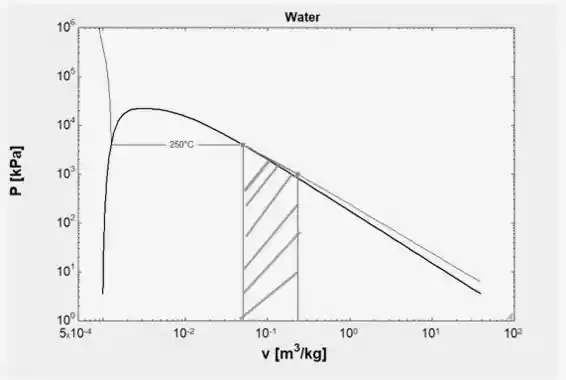
Estimativa do termo de trabalho da área no diagrama P-v

w 2 = 1 2 p 1 + p 2 v 2 - v 1

Com isso, nós temos que

w 2 = 1 2 1000 + 3973 0,5013 - 0,23268 = - 454   k J

Observação.: Note que não é uma estimativa precisa.

Resposta

w 2 = - 338   k J

q 2 = - 445,6   k J

Exercícios de Livros Relacionados

Água a 1000k P a e 250 ° C é levada ao estado de vapor saturado através de um processo adiabático em um conjunto cilindro-pistão. Determine a temperatura final, T , e o trabalho por unidade de massa.
Um conjunto cilindro-pistão contém água a 200k P a e a 200 ° C , com um volume de 20l . O pistão é movimentado lentamente, comprimindo a água até uma pressão de 800k P a . A carga sobre o pistão é tal
Um quilograma de amônia ( N H 3 ) líquida saturada, a - 20 ° C , está contido em um arranjo cilindro-pistão com mola. Calor é transferido de um reservatório a 100 ° C até que a amônia atinja a condiçã
Considere uma pequena pistola de ar comprimido a 250k P a e 27° C , com um cilindro de volume 1c m 3 . A bala age como um pistão inicialmente preso pelo gatilho. A bala é lançada de tal forma que o ar
Um conjunto cilindro-pistão, contendo oxigênio gasoso a 300K e 100k P a e com um volume de 0,1m 3 , é comprimido em um processo adiabático reversível até uma temperatura final de 700K . Determine a pr