Enunciado

Termodinâmica - Van Wylen- Ed: 6º - Capítulo 2.Problemas - Ex. 47

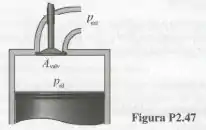
A área da seção transversal da válvula do cilindro mostrado na é igual a . Determine a força necessária para abrir a válvula sabendo que a pressão no cilindro é e que a pressão externa e .

Passo 1

Oi pessoal, tudo certo? Vamos analisar essa questão!

Para entender melhor esse problema, vamos fazer um diagrama de corpo livre das forças agindo na válvula:

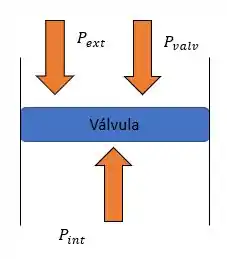
Podemos notar que para que o sistema esteja em equilíbrio, teremos que:

Onde, é a pressão interna da câmara no cilindro que vale . é a pressão externa exercida pela atmosfera na válvula e vale e é a pressão gerada a partir da força exercida na válvula.

Portanto:

Passo 2

Para calcular as forças devido às pressões tanto do fluido como da atmosfera no sistema, temos que:

Como já temos a área da seção transversal da válvula, é só substituir. Temos que:

Transformando em unidades do SI, temos que:

Resposta

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

A parte superior de um tanque de agua divide-se em dois compartimentos, como mostra a figura. Um fluido com densidade desconhecida e acrescentada de um lado, e no outro lado o nível da agua se eleva e

Repita o Prob. 1–83 para uma pressão manométrica de 40 k P a .

Observe o sistema mostrado na figura. Considerando que a interface salmoura-mercúrio na coluna da direita se desloca 5m m para baixo devido a uma variação de 0,7k P a na pressao do ar, com a pressão n

O piloto de um avião lê a altitude de 9.000 m e a pressão absoluta de 25 kPa ao sobrevoar uma cidade. Calcule a pressão atmosférica local daquela cidade em kPa e em mm Hg. Considereque as densidades d

A forca gerada por uma mola e dada por F = k x , ondek e a constante da mola e x e a deformação da mola. A mola da figura tem uma constante de mola de 8k N / c m . As pressões são P 1 = 5.000k P a , P