Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Termodinâmica - Sonntag, R.E. e Borgnakke, C. -Fundamentos da Termodinâmica- Ed: 1º - Capítulo 5.Problemas - Ex. 43

Um arranjo cilindro-pistão contém 5   k g de água a 100 ° C com x = 20 % e o pistão, de massa m p = 75   k g , repousa inicialmente sobre os esbarros, conforme mostrado na Fig. P5.43. A pressão externa é de 100   k P a e a área do cilindro é A = 24,5   c m 2 . Calor é então adicionado até que a água atinja o estado de vapor saturado. Determine o volume inicial, a pressão final, o trabalho, o calor transferido e mostre o processo num diagrama P-v.

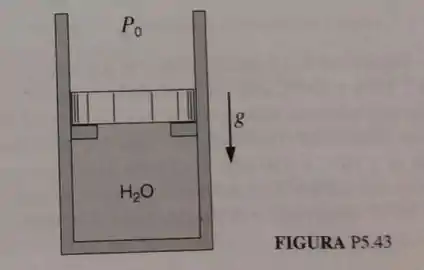
Passo 1

Fala pessoal, tudo certinho? vamos responder mais uma questão, então prepara o material e vamos responder!!

Nós temos os seguintes dados para a água, fornecidos pelo enunciado

T = 100 ° C

P a t m = 0,1   M P a

x = 0,2

A = 24,5   c m 2 = 0,00245   m 2

m p = 75   k g

m w = 5   k g

Neste problema temos 2 estágios. Um é o processo de volume constante e o outro é o processo de pressão constante. Para encontrar o trabalho total e a transferência de calor, temos que calculá-lo em cada processo e somar. Para facilitar, temos que olhar para o diagrama P-V para este problema.

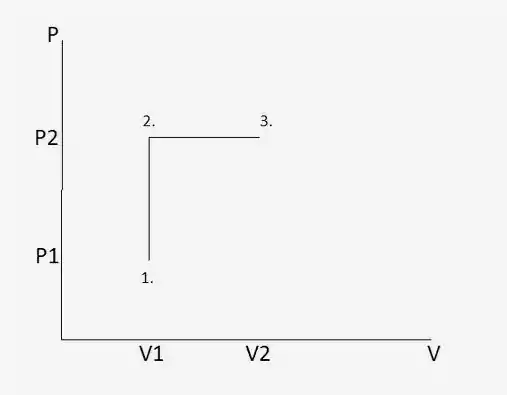
Passo 2

A pressão final é igual a:

P 2 = P a t m + m p ∙ g A

Fazendo a substituição

P 2 = 100000 + 75 ∙ 9,81 0,00245 = 400   k P a

Da tabela de água saturada B.1.1. correspondente a T = 100 ° C podemos obter volume específico e energia interna:

v f = 0,001044 m 3 k g

v f g = 1,67185 m 3 k g

u f = 418,91 k J k g

u f g = 2087,58 k J k g

O volume específico inicial é dado por:

v 1 = v f + x ∙ v f g = 0,001044 + 0,2 ∙ 1,67185 = 0,3354 m 3 k g

A energia interna específica inicial é dada por:

u 1 = u f + x ∙ u f g = 418,91 + 0,2 ∙ 2087,58 = 836,4 k J k g

O volume inicial é o volume do estágio 1-2 e é igual a:

V 1 = V 2 = v 1 ∙ m = 0,3354 ∙ 5 = 1,677   m 3

Passo 3

Da tabela de água saturada B.1.2. correspondente a P = 400   k P a podemos obter volume específico e energia interna:

v 3 = v g = 0,46246 m 3 k g

u 3 = u g = 2553,55 k J k g

O volume final no estágio 3 é igual a:

V 3 = v 3 ∙ m = 0,46246 ∙ 5 = 2,3123   m 3

O trabalho realizado no processo 1-2 é igual a zero, porque é um processo a volume constante:

W 1 - 2 = 0

Trabalho realizado no processo 2-3:

W 2 - 3 = ∫ P   d V = P 2 ∙ V 3 - V 2

Substituindo os termos,

W 2 - 3 = 400 2,3123 - 1,677 = 254,1   k J

O trabalho total realizado no processo é igual a:

W = W 1 - 2 + W 2 - 3 = 254,1   k J

A transferência total de calor é igual a transferência de calor nos processos 2-3:

Q = Q 1 - 3 = m u 3 - u 1 + W

Fazendo a substituição, nós temos que

Q = 5 2553,6 - 836,4 + 254,1 = 8840   k J

Resposta

V 1 = 1,677   m 3

P 3 = 400   k P a

W = 254,1   k J

Q = 8840   k J

Exercícios de Livros Relacionados

Um tanque rígido, com volume de 0,1m 3 , contém nitrogênio a 900K e 6M P a . O tanque é, então resfriado até que a temperatura atinja 100K . qual é o trabalho realizado e o calor transferido neste pro
Um automóvel apresenta área frontal de 2m 2 e se desloca a 80k m / h . A força de arrasto aerodinâmico no automóvel é dada por F d = 0,225 ρ A v 2 . Qual é a potencia necessária para realizar este mov
128- Um tanque rígido e selado contém amônia a 0° C e com título igual a 50% . O tanque é, então, aquecido até a temperatura atingir 100° C . Determine o estado final da amônia, o trabalho realizado e
Considere uma amostra de gás Hélio. Inicialmente, o volume da amostra, a temperatura e a pressão no Hélio são iguais a 0,025m 3 , 350K e 125k P a . O gás expande politropicamente n = 1,667 até que a p
Um conjunto cilindro-pistão contém oxigênio. Inicialmente, o volume interno do conjunto é 0,1m 3 e o ar apresenta temperatura e pressão iguais a 100 ° C e 300 k P a . O oxigênio é então comprimido, nu