Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Termodinâmica - Çengel - Termodinâmica - Ed: 7º - Capítulo 8.Problemas - Ex. 123

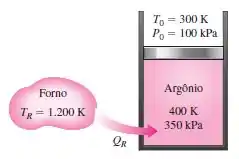
Um arranjo pistão-cilindro sem atrito, mostrado na Fig. P8-123, contêm inicialmente 0,01   m 3 de gás argônio a 400   K e 350   k P a . Calor e transferido para o argônio de uma fornalha a 1.200   K , e o gás expande-se isotermicamente até que o seu volume seja dobrado. Não há transferência de calor entre o argônio e o ar circundante atmosférico, que está a 300   K e 100   k P a . Determine (a) a produção de trabalho útil, (b) a energia destruída e (c) o trabalho máximo que pode ser produzido durante esse processo.

Passo 1

Vamos lá! A questão nos afirma que o gás argônio em um dispositivo de pistão-cilíndrico se expande isotermicamente como resultado da transferência de calor de um forno. A saída de trabalho útil, a exaustão destruída e o trabalho reversível devem ser determinados.

Assumindo que:

  1. Argônio em condições específicas pode ser tratado como um gás ideal, uma vez que está bem acima de sua temperatura crítica de 151   K .
  2. As energias cinéticas e potenciais são insignificantes.

Passo 2

Pronto já temos todas as informações necessárias, vamos para a análise. Tomamos o gás argônio contido no dispositivo de pistão-cilindro como o sistema. Este é um sistema fechado, pois nenhuma massa atravessa os limites do sistema durante o processo. Observamos que o calor é transferido para o sistema a partir de uma fonte a 1200   K , mas não há troca de calor com o ambiente a 300   K . Além disso, a temperatura do sistema permanece constante durante o processo de expansão, e seu volume dobra, ou seja, T 2   =   T 1   e V 2   =   2 V 1 .

Portanto para o item (a) A única interação de trabalho envolvida durante este processo isotérmico é o trabalho de fronteira quase equilíbrio, que é determinado a partir de

W = W b = ∫ 1 2 P d V = P 1 V 1 ln ⁡ V 2 V 1 = 350   k P a 0.01   m 3 ln ⁡ 0.02   m 3 0.01   m 3 = 2.43   k P a ∙ m 3

W = 2.43   k J

Este é o trabalho total de fronteira feito pelo gás argônio. Parte deste trabalho é feito contra a pressão atmosférica P 0 para empurrar o ar para fora do caminho, e não pode ser usado para qualquer propósito útil. É determinado a partir de

W s u r r = P 0 V 2 - V 1 = 100   k P a 0.02 - 0.01 m 3 = 1 k P a ∙ m 3 = 1 k J

O trabalho útil é a diferença entre estes dois:

W u = W - W s u r r = 2.43 - 1 = 1.43   k J

Ou seja, 1 . 43   k J do trabalho realizado está disponível para criar um efeito útil como, por exemplo, rodar um eixo. Além disso, a transferência de calor do forno para o sistema é determinada a partir de um balanço energético sobre o sistema a ser

E i n - E o u t = Δ E s y s t e m

Q i n - Q b , o u t = Δ U = m c v Δ T = 0

Q i n = Q b , o u t = 2.43   k J

Passo 3

Já no item b) A energia destruída durante um processo pode ser determinada a partir de um balanço de energia, ou diretamente de X d e s t r o y e d   =   T 0 S g e n .

Usaremos a segunda abordagem, uma vez que normalmente é mais fácil. Mas primeiro determinamos a geração de entropia aplicando um balanço de entropia em um sistema estendido (sistema + ambiente imediato), que inclui a zona de gradiente de temperatura entre o cilindro e o forno de modo que a temperatura no limite onde ocorre a transferência de calor seja T R =   1200   K . Desta forma, a geração de entropia associada com a transferência de calor é incluída. Além disso, a mudança de entropia do gás argônio pode ser determinada a partir de Q / T s y s , uma vez que sua temperatura permanece constante.

S i n - S o u t + S g e n = Δ S s y s t e m

Q T R + S g e n = Δ S s y s = Q T s y s

Portanto,

S g e n = Q T s y s - Q T R = 2.43   k J 400   K - 2.43   k J 1200   K = 0.00405   k J / K

e

X d e s t = T 0 S g e n = 300   K 0.00405 k J K = 1.22   k J

Passo 4

No item c) O trabalho reversível, que representa o máximo trabalho útil que poderia ser produzido W r e v , o u t   , pode ser determinado a partir do equilíbrio de esforço, fixando a destruição de esforço igual a zero,

X i n - X o u t - X d e s t r u í d o = Δ X s y s t e m

1 - T 0 T b Q - W r e v , o u t = X 2 - X 1

= U 2 - U 1 + P 0 V 2 - V 1 - T 0 S 2 - S 1

= 0 + W s u r r - T 0 Q T s y s

desde Δ K E   =   Δ P E   =   0   e   Δ U   =   0 (a alteração da energia interna de um gás ideal é zero durante um processo isotérmico), e Δ S s y s =   Q / T s y s para processos isotérmicos na ausência de qualquer irreversibilidade. Então,

W r e v , o u t = T 0 Q T s y s - W s u r r + 1 - T 0 T R   Q

= 300   K 2.43   k J 400   K - 1 k J + 1 - 300   K 1200   K 2.43   k J

= 2.65   k J

Portanto, a saída de trabalho útil seria 2 . 65   k J ao invés de 1 . 43   k J se o processo fosse executado de forma totalmente reversível.

Resposta

a )   1.43   k J

b )   1.22   k J

c )   2.65   k J

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Em um bocal de vapor adiabático o vapor entra a 300k P a ,150° C e 45m / s , saindo como vapor saturado a 150k P a . Calcule a velocidade de saída efetiva e máxima. Considere T 0 = 25° C .
Gases quentes de exaustão que saem de um motor a combustão interna a 400° C e 150k P a a uma vazão de 0,8k g / s devem ser usados para produzir vapor de água saturado a 200° C em um trocador de calor
No inverno, as superfícies interna e externa de um vidro de uma janela de 0,5c m de espessura e 2m ×2m estão a 10° C e 3° C , respectivamente. Considerando que a taxa de perda de calor pela janela é d
Para controlar uma turbina a vapor isentrópica, uma válvula de estrangulamento é colocada na linha de vapor que conduz à entrada da turbina. Vapor a 6M P a e 700° C é fornecido à entrada do estrangula
Uma turbina adiabática opera com ar entrando a 550k P a e 425K e saindo a 110k P a e 325K . Calcule a eficiência de segunda lei dessa turbina. Considere T 0 = 25° C .