Enunciado
Termodinâmica - Çengel - Termodinâmica - Ed: 7º - Capítulo 10.Problemas - Ex. 79
Na caldeira de uma usina de cogeração, gera-se vapor a 600 psia e 800 °F a uma taxa de 18 lbm/s. A usina deve produzir energia enquanto atende os requisitos do processo a vapor para uma determinada aplicação industrial. Um terço do vapor saindo da caldeira é estrangulado para uma pressão de 120 psia e direcionado para a unidade de processamento térmico. O resto do vapor é expandido em uma turbina isentrópica até uma pressão de 120 psia e também é direcionado para a unidade de processamento térmico. Vapor deixa a unidade de processamento térmico a 240 °F. Desprezando o trabalho da bomba, determine (a) a potência útil produzida, (b) a taxa do fornecimento de calor de processo e (c) o fator de utilização dessa planta.
Passo 1
Beleza, antes de começar o exercício, vamos ilustrar o diagrama da usina de cogeração descrita no enunciado:
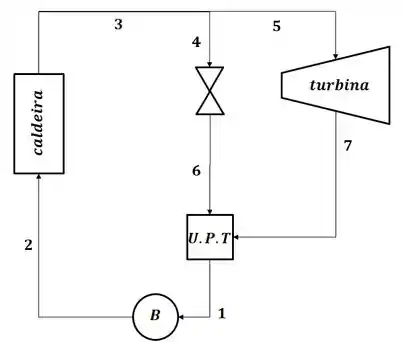
Tá legal! Agora, como o enunciado nos forneceu informações no sistema inglês, vamos converter os dados para o sistema internacional, então, temos:
Agora o que devemos fazer é pegar as propriedades do fluido nos pontos de interesse com os dados fornecidos no enunciado, então, com a ajuda das tabelas termodinâmicas do apêndice A, temos:
Com esse valor, podemos encontrar o trabalho específico exigido pela bomba e depois encontrar a entalpia no ponto 2, então teremos:
E, aplicando o equilíbrio de energia específica para a bomba 1, temos:
No entanto, o enunciado nos disse para desprezar o trabalho da bomba, então teremos:
Agora, continuando com as propriedades, temos:
E, através do diagrama do passo 1, sabemos que temos as mesmas condições nos pontos 3, 4 e 5, então, teremos:
E, como temos o dispositivo de estrangulamento, sabemos que podemos considerá-lo como isentálpico, então também temos:
Agora, para o ponto 7 teremos:
Passo 2
Agora, com todas as propriedades encontradas, podemos calcular o trabalho líquido produzido pelo sistema. Esse trabalho será só o trabalho da turbina, já que o enunciado nos disse para desprezar o trabalho da bomba. Então, esse trabalho pode ser encontrado pelo equilíbrio de energia na turbina, que resultará na diferença de entalpia na mesma, então, teremos:
Substituindo os valores conhecidos, temos:
Passo 3
Agora, para resolver a letra b), vamos aplicar o equilíbrio de energia para a unidade de processamento térmico, onde teremos então:
Como temos regime permanente, então , dessa forma a equação acima se torna:
Então, escrevendo em função das entalpias e vazões mássicas, teremos:
Então, substituindo os valores conhecidos, temos:
Passo 4
Agora, para calcular o fator de utilização, precisamos do calor que entra no sistema pela caldeira, então teremos:
Substituindo os valores conhecidos, temos:
Então, o fator de utilização será: